Оглавление:


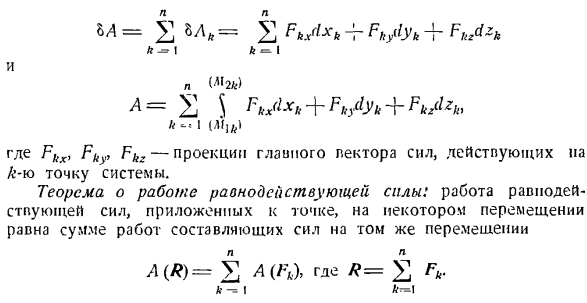







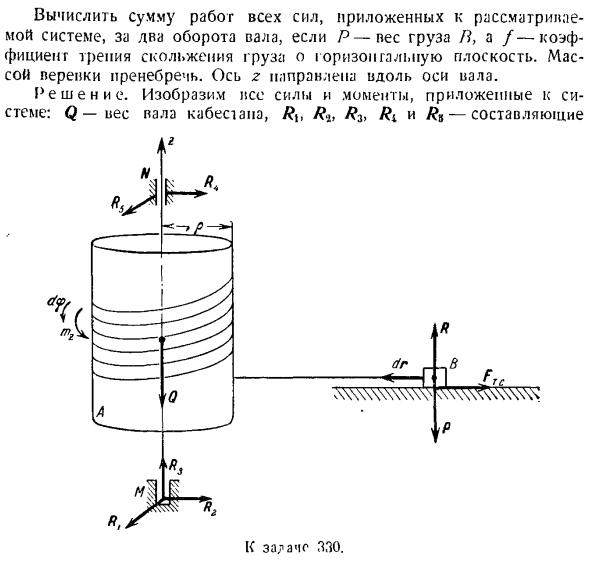




































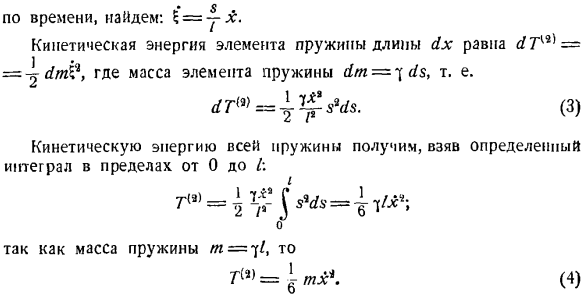



































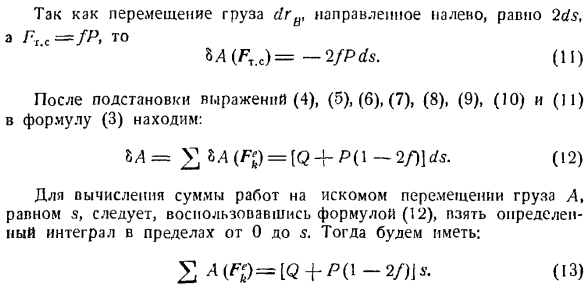





























Теорема об изменении кинетической энергии системы материальных точек
- Теорема об изменениях кинетической энергии материальной точечной системы 1°.Работа власти. Работа постоянной силы относительно линейного перемещения называется скалярным произведением силы и перемещения пектата. То есть работа будет равна Косинусу произведения коэффициентов силы и перемещения и угла между ними: А = ф•= ф±Р соѕ(Ф} ХС) ЛТ ’ — младший(ми и Ми в начале и финале Положение точки мой Dg-это вектор смещения
точки. 134.(Рис. 134, 135) при переходе от MX к единице измерения: кг * м. фундаментальная работа переменной силы равна скалярному произведению силы и вектору фундаментального смещения oA = / w / R. А-0 Зл ^ м, J г м; Рисунок 135. Базовые перемещения д-р направлена вдоль касательной локуса в данной точке(рис. 136).Начальная школа работает только в определенных случаях Девятьсот один 6г м Компания LG мг а: А / р = а \ АИ = Урр-ол.2 = /(cos cp-cos следовательно А (Р)=
Другие начальные положения точечной массы маятник Людмила Фирмаль
-пи (с COS ® и. Подставляя 4(I), вы можете видеть, сколько труда вам нужно. 2 АК =-п /(потому что инфляция-что-cf2) Эта задача также может быть решена путем вычисления суммы работы силы при вращении маятника вокруг оси z, проходящей через точку усиления О перпендикулярно плоскости figure. In в этом случае основная работа силы будет равна b, −4 = tnz-dy. Где m-главный момент относительно оси z вращения силы, приложенной к точечной массе. если момент
реакции нити R относительно оси z равен нулю, а момент массы P относительно оси z равен-PI sin 9 (момент отрицательный, а его направление противоположно направлению положительного опорного угла поворота 9), то получим mz = — PI sin 9, таким образом, Для вычисления искомой работы необходимо взять определенный интеграл в диапазоне от 9 до 9-9. < м.4 = 5 тг = — П / ^ грех 9 х / 9 = Ви — П /(Косинус 9、- потому 9-2). Расстояние s наклонное plane.
- In начальное положение, система была остановлена. Ролик A, блок B и цилиндр D считаются непрерывными однородными цилиндрами. Вес веревки игнорируется. Решение: Поверните ось s Через центр инерции c \ролика d, параллельный линии максимального наклона верхней наклонной плоскости. согласно положительному направлению оси s, угол поворота ролика A, блока B и цилиндра D равен
k /) = H3 / 3k = £ = P3 cos p / 3k и используйте формулу (2), чтобы получить: = — П / / ГКЗ-что?< / А (8) Следующий.: М№)= ЖВ) = О (9) (Точка действия и остальная сила).Наконец, есть следующие: М(/ я)/ л поскольку m = ay, снова используйте выражение (2) и запишите его следующим образом: ба(м)= ^ ДС. (10 )) И затем… М(ф; п)=: м(л^) =0.(11) (Ролик A и цилиндр D будут катиться без скольжения.) (4)、(5)、(6)、(7)、(8)、(9)、(10)、подставляя (11) в Формулу (3), находим выражение основной работы внешних сил системы. БА = <п — Пы (грех + потому что;- — ^(Sin 3 cos (12) Для вычисления суммы работы внешних сил системы при конечном перемещении s воспользуемся формулой (12).
Кинетическая энергия конечного положения: T * = Tn + T. 2P + Tsh(15) V указывает желаемую скорость точки C Людмила Фирмаль
Интеграл ределина формулы в диапазоне 0-s (12).Мы также имеем rjcpi-s. после внедрения, вы получите: л = 2 ″ г-2Р ’(грех * + Т, потому что)- — Па (Син?+ и cos? А (13)) Приступим к расчету кинетической энергии этой системы. Система состоит из 3 масс (роликов.4, блок B, цилиндр d). В исходном положении, система была остановлена. 7 \ = 0.(14) .Поскольку трос
не деформируется, скорость оси С1 равна скорости точки на ободе блока В и скорости точки К на ободе цилиндра D. в-р, ш, — р ^ я = 2gl о) 3 = 2vc(10) Где ж / о> .2 и w3-угловые скорости звена A, блока B и цилиндра D соответственно (скорость v точки K цилиндра D следует рассматривать относительно мгновенного Центра eP3 цилиндра. Цилиндр d C3 равен половине скорости точки K). Кинетическая
энергия звена а, выполняющего планарное движение, вычисляется по формуле ты = ДХ—/с «;. П Р Г В Предположим, что М {= ВР-з = в, ЛР-1, 1′ -, з,= -. Р «Ш 21!Г、 = < 17> Кинетическая энергия блока Wu, вращающегося вокруг неподвижной оси, равна Курс t2i = 2 П В В Здесь = ω2=-(см. формулу (1G))… ХН = \ Ф ^ Ы 8) Кинетическая энергия цилиндра D, совершающего плоское движение, рассчитывается
по формуле: Деревья= \ Здесь = vCi = r2, = aa = 72 ^- (см. уравнение (16)). Так… Найти выражение кинетической энергии системы в конечном положении путем введения (15), (17), (18) и (19) в уравнение. 7и = 1 ^(l2Pl + 4Pi + 3па). (20 )) Формула (1) (13), (14), и (20)подставляется и определяет искомую скорость v инерционного центра ролика a. ЛГ 2 РХ \ так что + потому что а) — Р3(грех?- F COS A м> = 2 | / в_ТГУ / _ \ _ З. Если радикальное выражение является положительным, то движение возможно. Задача 354. на рисунке а показана сборка автоматического устройства, состоящего из 2 пар коленчатых валов
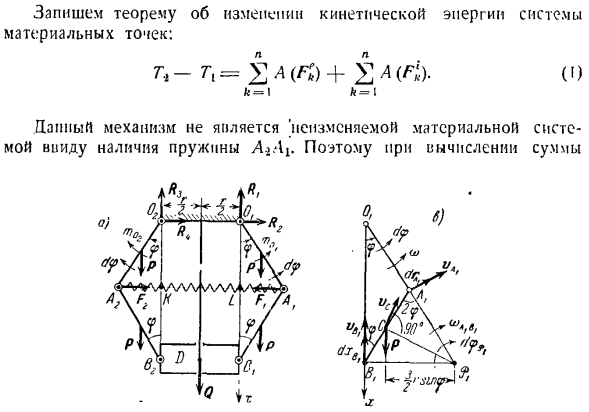
Ol / 4, fl1 и О^^ ^ ^ с общим ползуном массы Q, перемещающимся в вертикальной направляющей. Шатуны A \ B \ и Af ^одинаковой массы P и длины r, с кривошипами 0 \AX и 0 * A2.Кривошип o, y o перпендикулярен плоскости чертежа. J-это、 Симметричная вертикальная ось механизма на расстоянии£. для придания жесткости механизму кривошип A \и A. рога g соединены между собой пружинами с модулем упругости S. At исходное положение
механизма, кривошип и шатуны располагались вертикально, а пружины не деформировались(см. рис. 6).Под действием постоянного крутящего момента t кривошип отклоняется от вертикального положения и поднимает ползунок (I).Если кривошип отклонен на угол 9 от вертикали, то кривошип Ojj и 0,2 при положении механизма? Определяет угол поворота скорость вращения 4a. In в исходном положении механизм был остановлен. Кривошип и шатуны считаются однородными болота. Масса пружины игнорируется. Решение. направьте ось x вертикально вниз от точки 0.Положительное направление опорного угла cp: для правого
кривошипа-против часовой стрелки, для левого кривошипа-по часовой стрелке. Напишите теорему об изменении кинетической энергии материальной точки : Т — ±А (Центр). (Я) к = \ к = \ Этот механизм не является неизменной материальной системой из-за наличия пружин A ^ C. Поэтому при расчете суммы Ф-о. LLLLOL D 1_ Рама 3 — > 4. Для работы силы необходимо учитывать не только внешнюю силу(2 кривошипа, 2 шатуна, сила тяжести ползуна D, составляющая оси кривошипа, анти-сила Rl}/?。>, Р ^ .R ^уравнивает моменты mQi и w0i, приложенные к кривошипу, но внутренние упругие силы пружины Fi и / \ 2(поскольку кривошип и шатун
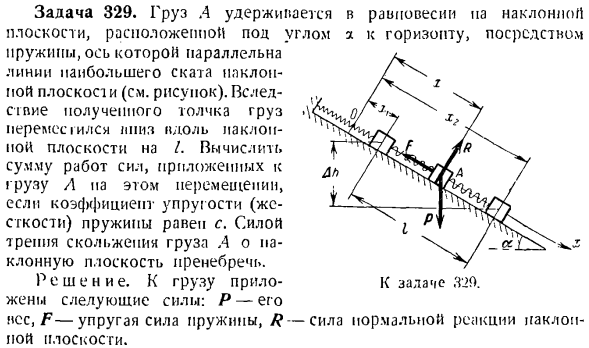
полностью жесткие, сумма работы соответствующих внутренних сил равна нулю, поэтому другие внутренние силы можно игнорировать).Все вышеперечисленные силы показаны на рисунке. один. Дайте базовое угловое смещение dy к кривошипу 0 \ LH в положительном направлении опорного угла o для расчета Сумма основных работ внешних и внутренних сил системы па б) Задача 329.Нагрузка а уравновешивается на наклонной поверхности под углом х относительно горизонтальной плоскости пружиной, ось которой параллельна следующему направлению. Максимальный уклон Пойте плоско (см. Фото).Следовать — / n. ^ Ударная нагрузка ’
sNtJZ / хУ Двигайтесь вниз по склону — ^ wws / ’ Я пою в самолете. вычислить F^ ^ вра ^ Л О. ^ / Количество труда, приложенного к Нагрузка и, в этом движении, / » ML g,. / Модуль упругости Размер звука) равен S. принудительно^ ^ t Нагрузки пизды и Па — / _ а о Наклонная плоскость игнорируется. ^ год Solution. To соседняя нагрузка. Следующая власть жены: П-он Вес, сила упругости F-пружины, вертикальная сила реакции R-наклонной плоскости.
Это движение: вл = м; м т ^ м(/ =•/)= 3 <4(polAi)-(по, А.(ПВ+ ж) + ^ РЛ) + Ла (СД + Ш)• — я- + 8 л(/?.) —ЛЛ(Р5)8 л(Р3) — 1-8 л(Р4)+ 8л(m0j)+ Учитывая симметрию механизма относительно вертикальной оси и системы приложенных сил, выражение основной работы упрощается. ЛА = В 8А(ч) −2 Ла (Ф’) = Н(Р ^ + ПА (ПД | Н|) + — п-пр (м)+ (())+ Дж-26.4 ( *) -}- 28Л (М)+ 2а (Т). (2) Кривошип 0 | .4 (попрощайтесь с неподвижной осью Ox%, перпендикулярной плоскости рисунка. И так оно и есть.、 Л (POiA)= — моль (пола>) Л <Ф- Момент силы
и направление углового перемещения(1 <® — обратное.// / / zQi = = R-t грех В, мы найдем: Шатун D,£совершает плоскостное движение. Мастерская мгновенной скорости расположена на пересечении перпендикулярных линий. Точки A \и Z? Ва и АУ (см. рис. Б). Поскольку это OlAt = A&it = r, он становится drAi =OxAld®= Ax & xd ^, следовательно=и dygp.^По Часовой Стрелке. Следующий Работа отрицательная, так как угловой момент RA n и направление углового
перемещения противоположны. И я думаю, что Н9 \ р р ы н?» WLP по ^^ — Дж / Vsin ^ ДФ. (4 )) Вычислите базовую гравитационную работу Q для слайдера D. определите dx ^от C, A (Q)= коэффициент Qdxnr. iffsd т ь! призраки-с дх / ’ml Р: д-р л ^ = о ИД? = Р 1,/,, + T0.In в исходном положении механизм был неподвижен. Т \ =0.(13 )) В конечном положении механизма, если кривошип отклонен вертикальной фракцией R, угловая кинетическая энергия равна Т * = 2TU1Lg \ — \ GG1L113g — ти. (И) Кинетическая энергия кривошипа, вращающегося вокруг оси phepo рассчитывается по формуле РГ- Где I0l = — t a(где o-
искомая угловая скорость.И так оно и есть.、 7 * 20 ^ = = (15) Кинетическая энергия шатуна A \ B>, который совершает планарное движение, равна 2 afre+ 2 k ^ ’ xjir В этом деле Р Пр- М = ДЖ > > С = Т£-07) Скорость центра инерции шатуна C ^ ^равна мгновенной скорости Центра ε?(См. Рисунок C.) Треугольник A ^ C: A, C = A^, = A, 0i = R. И так далее.、 С0\ = » [/^»ГТ» «2r7c () s = v’ о-4 COS 2 < p»’ = 7 * 20, л,== » в Гогр L 01-и С К Р
И значение n, рассматриваемое подстановкой выражения ’(18) ва = 0,.4, Если w = po, это выглядит так: ВК ^ р-и J \ / ’\ Я + 8sin ^. (19) Угловую скорость шатуна можно легко определить: это отличный способ начать работу. ,, Иначе говоря =(2°) Направление и w противоположны(см. Рисунок C). Замена(17). Из (19) и (20) и (16) получаем уравнение кинетической энергии шатуна, L \ H. = ’(1 + 8 sin4?)- 1-’Щ-РФ = — 6С б, н в(2.) Кинетическая энергия постепенно движущегося ползуна D рассчитывается по следующей формуле: Tст = \ 1° — ВХ(22) Для поступательного движения vd = vh {.Скорость точки B определяется с помощью мгновенного центра скорости (см.
Рисунок C). Би & Т vAl = 0, / 4, ω= rco. = 0, А= Р ВХ&х = 0,<^ 1 грех 9 = = 2rsin 9 тогда vD-vn {=2gf sin 9(23) Подставляя выражение (23) в (22), получаем: ТВ> = * — рвснв (24) г Для этого напишите уравнение движения точки= 2r cos 9 и возьмите производную по времени. ХВ {= ВТХ—2 / −9 грех 9 = — 2 Руи грех 9. Подставляя формулы (15), (21) и (24) в формулы (14), можно увидеть кинетическую энергию механизма и его конечное положение. 7 = я-1 /> — Б-3(п-ф В) грех ’?!(23)) Остоея
подставляет Формулу (1) вместо формул (12), (13) и (25), а алгоритм определяет! Требуемая угловая скорость вращения кривошипа. 11 совершенство: R > \ потенциальная энергия. Когда система материальных точек воздействует на силу, которая однозначно определяется положением точки, система движется через силовое поле. Если работа силового поля определяется начальным и конечным положением точек системы и не зависит от формы
траектории движения этих точек, то силовое поле называют потенциальным (консервативным). Потенциальная энергия материала тонко определяется действием масла. Действие нефти осуществляется силой поля при перемещении этой точки из определенного положения в нечеткое положение. Потенциальная энергия зависит от положения точки в поле. 11 = II(А -, Г, Д). Выберите опорную точку О для сваи и деформированной пружины и направьте ось xy параллельно линии максимального наклона склона. В положении равновесия нагрузки пружина вытягивается и становится Dst. если записать сумму проекций всех сил,
приложенных к нагрузке по оси x, то получится Psina-Pcr = 0.In другие слова летнее время.^ = (Приблизительно. Желаемый объем силовой работы имеет форму (2) Поскольку нагрузка а находится ближе к поверхности Земли, то работа гравитации положительна. Рассматривая A (P)= PMi; A / / = / stna, вы можете увидеть следующее: A (P)= PI sin a. (3) Работа упругой силы пружины определяется по формуле л если рассматривать х {= ДСТ и ХЖ = ХХ — (- /=ДСТ /、 A (F)= — o’c ^ em-I).И затем) Потенциальная энергия системы
материальных точек является функцией координат всех n точек системы. Λ=(г, у, yxk, ykt zk,…xni йни ЗН). Эквипотенциальная поверхность (ровная поверхность) — это геометрическое расположение точки поля, в которой потенциальные аннапиры имеют одинаковое значение. Второй(х, Z) = с При перемещении материальной точки в потенциальном поле сила, действующая на поле, равна разности между начальным положением точки и потенциальной энергией конечного положения: l = TG, — но. Сила, действующая на потенциал YL, направлена перпендикулярно эквипотенциальной поверхности в определенной точке
в направлении, в котором потенциальная энергия уменьшается. Проекция на ось этой силы будет равна частной производной потенциальной энергии относительно соответствующих координат с противоположным знаком: _ p p О ГУ-серийные ’ 0 г• Где F = FJ + FyJ + Fgkt, то есть выпускник I. 13 случаев в системе из n материальных точек П _ ДП П _ О, _ ДПМ _ 0 Учитывая проекцию силы Fx% Fv F Fg на ось декартовых координат, и если необходимо
определить, является ли сила F = Fxi- \ Fyj-4-F ^ k силой (потенциалом), действующей на потенциальное поле, то определяется равенство силы F. DFX с _ _ DFX с сайта dfy _ dGy d_Fy _ тфп делать Ф) Х〜 ’ДГ ДХ’ ДГ ду ’ d если эти уравнения также выполняются, то сила F является потенциальной. В противном случае сила связи подсознательна. Основная задача потенциальной силы равна полной производной потенциальной энергии, взятой по противоположному знаку: О =-
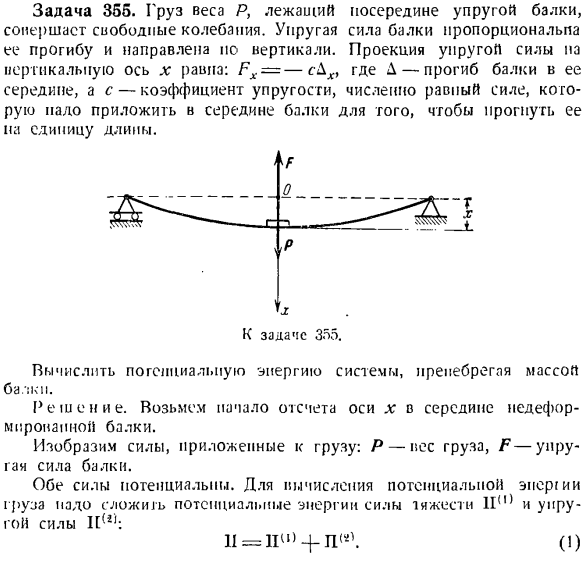
файлов. Таким образом, в случае потенциальных сил основная генерация силы bA может быть представлена dA. Расчет потенциальной энергии материальной точечной системы является одним из этапов решения задачи при использовании теоремы об изменении кинетической энергии, уравнения Лагранжа типа 2 и др. 1. Проблема 355.Нагрузка от нагрузки Р в центре упругой балки вызывает свободные колебания. Сила упругости балки пропорциональна ее отклонению и направлена перпендикулярно.
Проекция силы упругости на вертикальную ось x выглядит следующим образом: Вычислите потенциальную энергию системы, игнорируя массу пучка. Решение. Возьмем начало координат оси x, которая находится в центре недеформированной мирояпной балки. Указывает усилие, приложенное к нагрузке. P-вес груза, F-сила упругости балки. Обе силы являются potential. To вычислите энергию положения G
Потому что потенциальная энергия-это работа потенциальной силы при перемещении материальной точки из определенного положения в ноль、 П (,, =- РХ.(2) Потенциальная энергия силы тяжести P отрицательна, когда необходимо переместить груз вверх, чтобы перейти из определенного положения в пулю. Узнайте ниже: W31 =. (3) Энергия положения упругого пучка положительна. Формулы(2) и (3) (!) Подставляя), находим искомое выражение потенциальной
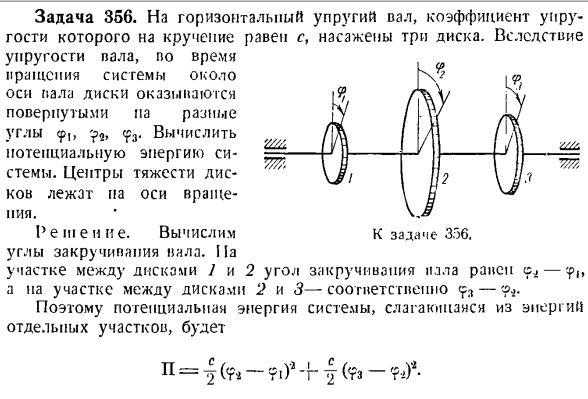
энергии системы. Задача 356.3 диски крепятся к горизонтальному упругому валу, модуль упругости которого равен S. By упругость вала、 Вращение системы вокруг оси вала, диск вращается под разными углами 9, sr3.To вычислить Потенциальная энергия системы. Центр тяжести диска находится на оси вращения. Solution. To вычислить Угол наклона. Для Площадь между дисками/и 2, угол кручения станины-равна cri, а в области между дисками 2 и 3 соответственно cp3- Таким образом, потенциальная энергия
системы, состоящая из энергии отдельных участков, будет равна: Голы: 356 6°. 3 и о, и С, и механическая энергия. Если все силы, приложенные к системе материальных точек, являются потенциальными, то сумма кинетической энергии системы и потенциальной энергии постоянна. 7H-P,= 7; 4-P.、 Механическая энергия уменьшается, потому что она менее устойчива к потенциалу, как механизмы и машины. Эта энергия расходуется на работу непотенциальных сил и в других видах энергии (например, n-
теплота).Поэтому закон сохранения механической энергии в этих случаях не применяется, а поддержание устойчивого состояния машины или механизма требует притока механической энергии извне. Проблема 357.Расчета полная механическая энергия физического маятника массой Р В зависимости от угла отклонения
. (3) Используя формулу (3) для расчета необходимого объема работы всех сил при 2-х оборотах тон-оси вала требуется определенный интеграл до предела.
Проблема 331.Колеса радиуса r катятся без скольжения по прямому горизонтальному рельсу под действием постоянной силы F, параллельной рельсу, а постоянный крутящий момент t добавляется к центру тяжести C. Если ось колеса C перемещается па s, вычисляют сумму работы всех внешних сил. Трение игнорируется. Определение: представляет вес P колеса. Внешняя сила приложена к колесу: P-вес колеса, R-нормальная реактивная сила рельса, F-движущая сила, сила
пары моментов t. Так как колесо совершает плоское движение, то мы рассчитываем основную работу всех внешних сил с точкой С в качестве полюса по следующей формуле: (Приблизительно. БА =Вэ•(Ирк tcgC д>?。 Рассматривая R = — P, мы можем видеть, что основной вектор равен Ve = F, и поэтому Ve * drQ = FdrQ. Так как моменты силы P, F и R на оси zt, проходящей через точку C, перпендикулярную материальной плоскости колеса, равны нулю, то основным моментом внешней силы на оси z является метка C = M.
Формула (1) принимает вид: BA = Fdrc + TFF. (2) 5Вт \ Ж \ \ \ \ Ш \ \ Проблема 33! В зависимости от ситуации, о которой идет речь, колеса не скользят и roll. So, центр мгновенной скорости находится в точке соприкосновения колес и рельсов, а drQ — это d? Зависимость ДРК■■= г ды. Итак (выражение (2) записывается следующим образом: ба = Ф. Ф + М> СРБ. (3) \ ’Д, С в) Для вычисления искомой суммы работы всех внешних сил необходимо взять определенный интеграл
от bA с пределом от 0 до s. А = (р +?14gs = [М -: П (4) В обзоре теории отмечено, что любая точка твердого тела, совершающая плоское движение, может рассматриваться как pole. To объясните это положение, точка C вместо полюса момент скорости центр c? От 5 до use. In в свою очередь, основная работа всех внешних сил зависит от формулы Х \ = в ’- ДРГ, — ynfjp <л’, (5) Потому что скорость точки колеса равна пуле,= = =Тогда dr
= ’ Vlcpdt = 0, и уравнение (5) принимает вид БА = » > уй?。 (Г) главные моменты внешних сил на ось Z являются Через мгновенный центр скорости перпендикулярно неподвижной плоскости、 Таким образом, выражение (6) можно записать в виде: BA =(g’R + m) и? учитывая, что drc = r dy, вы можете увидеть следующее: BL = / r-R’N) 1, РФ. То же самое выражение основной работы было получено выше, когда точка С была взята против полюсов (см. уравнение (3)). Сравнивая оба варианта расчета Ба, можно увидеть, что более
разумно получить точку ОП колеса из полюсов. Работа силы является полной производной от конкретной координатной функции (см. случай потенциального поля ниже). Представление основной работы переменной силы проекцией силы на ось декартовой координаты имеет вид、 БА = ф-д-р = Fxdx-Ф I7ydy-Ф F2dz、 Куда? Ф = Ф. + Ф. + ф£K и Р = ИВС + Дый- ’ rdzk. Работа переменной силы над конечным перемещением по траектории кривой равна интегралу кривой, взятому по дуге кривой из скалярного произведения вектора силы и фундаментального перемещения из M]. (Звуковая частота. .
(АККРЕДИТИВ^) А = \ ф-д = ^ ф д-р сов(ф, д). (Ми) (все) (Интеграл называется кривой. Это неудивительно, поскольку сложение осуществляется вдоль кривой траектории, и в разных ее точках направление тангенциального фундаментального смещения dr различно.) Выражение работы переменной силы на конечное перемещение по криволинейной траектории через проекцию сил на ось декартовых координат имеет следующий вид: (Звуковая
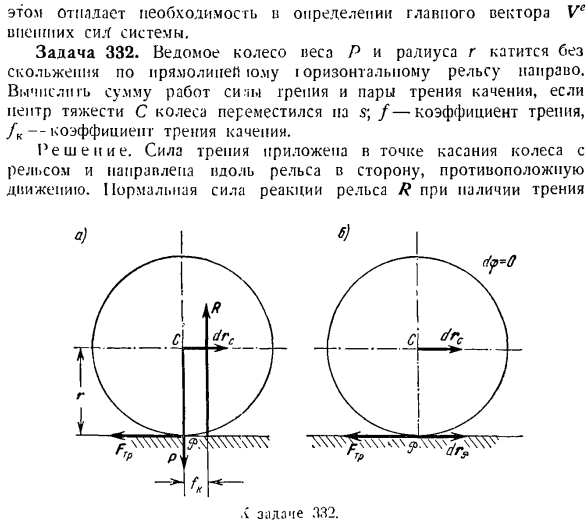
частота «) А — \ Fxdx- \ — л: ыды + Fzdz. Мельница) Когда система сил приложена к точкам материальной системы, работа равна сумме работ всех сил Р. Рисунок 136. М Это устраняет необходимость определения основного вектора Ve для внешней системы si A. Задача 332.Управляемые колеса веса P и радиуса R катится по прямой без скольжения вправо горизонтальную рейку. C если центр тяжести колеса перемещается на s, вычислите сумму работы пары трения и трения качения. / — Коэффициент трения,/ к-коэффициент трения
качения. Решение. Сила трения приложена в точке соприкосновения колеса и рельса, направленной вдоль рельса в направлении, противоположном движению. Вертикальная направляющая сила реакции R, когда возникают трения l задача 332. Качение на стороне движения, отделенной от обычного давления на расстоянии, равном коэффициенту трения качения/ к (в этом случае давление нормального равно весу колеса Р), образует пару колесных масс
и трения качения(см. рисунок а). Основная работа силы трения F1 [t = fN = fP равна пуле. Правда, если колесо наклонено без скольжения, то центр мгновенной скорости находится в точке соприкосновения колеса с рельсом. Сила трения F1 [t приложена к колесу в точке, которая всегда совпадает с мгновенным центром скорости и движется с wheel. So, выражение N = Fr? Сила трения, рассчитанная в ’ Vep так как v <p — = 0, то она равна нулю. Принимая это во внимание=мы получаем М(Фип)=0.(1) Основная работа пары трения качения отрицательна. Момент пары трения качения находится против часовой стрелки、
Противоположно направлению угла поворота колеса(когда колесо поворачивается вправо, оно вращается по часовой стрелке): Отставание, к = — / лы. К-ТФ?。 Сила, содержащаяся в паре трения качения, равна P9 как метод, а плечо пары равно коэффициенту трения качения/ k, следовательно, tshrm = P / k, следовательно, d / 1m> k =-P / k ДРК = РД = drc (см. Рисунок Tf). Так… 8LT. C = — FTX dr ^ =-/ Pbrct В рассматриваемом случае сумма основной работы равна m = mTL + mT4-fPdrc. Если вы интегрируете в диапазоне от 0 до S, вы увидите следующее: кадр. Задача 333.v = определяет выход заряженных частиц, летящих со скоростью 60 000 км/с. Под действием
электромагнитного поля F = 5-10 «10 г. Решение. Мощность частиц рассчитывается по формуле Jsf = Fv. Если скорость частицы выражена в М / С, а сила-в кг, то: ti = 6-10O7 м / с / 7 = 5.10 «13кг、 Иначе говоря А/ = 6•107•5■10 „13 = 3•10-6 КГМ. 2°.Кинетическая энергия материальной точки и сочетание g, m и материала кинетическая энергия материальной точки равна половине произведения массы точки на ключ Т-1■я Соотношение его скоростей: 7 = ТВ. Единица измерения * кинетическая энергия кг-м. кинетическая энергия является одной из мер движения точки массы. 1. Кинетическая энергия системы материальной точки дождя есть сумма кинетической энергии всех материальных точек системы. Н. Н. Н. T = V 7 * = 2 “ rnkv%. ч ^ л U л Кинетическая энергия положительна, если скорость всех точек
не равна нулю одновременно. 1 / в теореме Кента кинетическая энергия системы материальной точки дождя есть сумма кинетической энергии всех масс, движущихся со скоростью центра инерции, и кинетической энергии системы при всех относительных движениях по поступательным координатным осям с началом координат r центра инерции.: н м=] 2 МВЛ-я-7р, где m= -, г в МКВ \ с k = I (v / {(. — относительная скорость N-й материальной точки относительно центра инерции.) Кинетическая энергия твердых тел рассчитывается по формуле: А) в поступательном движении: 7 ’=.> Alv, где a \ — масса твердого тела, а v-скорость этой точки. б) при
вращении вокруг неподвижной оси: T = — y / 2 , 1d- Момент инерции твердого тела относительно оси вращения, r}и w, является угловой скоростью вращения. в) для плоского движения: 7 = / um—/ -; y, og, Λ1-масса VQ твердого тела-это скорость движения центра инерции по нему, Igr-момент инерции твердого тела относительно оси z, которая проходит центр инерции перпендикулярно неподвижной плоскости,и мгновенная угловая скорость вращения к. Кроме того, в случае плоского движения кинетическая энергия равна Вычислить по
формуле.Где I ^ — момент инерции. Объект относительно оси, проходящей через центр скорости момента перпендикулярно неподвижной плоскости. Поэтому, когда твердое тело движется, момент инерции 1 cp%обычно является переменным. d) при вращении вокруг неподвижной точки: T = / oD, где / — Момент инерции твердого тела относительно мгновенной оси, ω-мгновенная угловая скорость (/- значение переменной, поскольку мгновенная ось изменяет свое положение, когда твердое тело вращается вокруг неподвижной
точки). Если выбрана начальная точка движущихся осей x, y, z, связанная с телом неподвижной точки O、 Т = Дж СХ + С-З-2(г » г°* ~~〜 Где hL, a> y-проекция мгновенной угловой скорости на соответствующие оси. так как 1ug = 12X = 1x = 0, если ось x, y, z является главной осью инерции твердого тела в неподвижной точке O、 м = 2 О * х+ // // 4 + д) общий случай движения твердого тела. Т = — МВ-с + tg / C » где где A1-масса твердого тела, VQ X-модуль скорости центра инерции,/ c-момент инерции к оси инерции, а W-мгновенная угловая скорость. / Если выбрать начальную точку перемещения
координатных осей x, y, z центра инерции、 м = Дж МВ * с +〜(iyx-ф / г»О],+ данные-21ug (o^, <oi-проекция мгновенной угловой скорости на соответствующие координатные оси. если ось x, y, r является главной центральной осью инерции, так как x2 = lzx=] xy = 0、 Т = Дж проектирования MVC * Т Дж Vx0) х + ( / » } +(ж Расчет кинетической энергии массовой системы является одним из этапов решения задачи подготовки уравнения Лагранжа типа 2 (см. X, см.§ 6 ниже) или расчета потери кинетической энергии при ударе с использованием теоремы об изменении кинетической энергии массовой системы (см. X, II, 1 ниже). При расчете кинетической энергии
Ввести в систему и рассчитать кинетическую энергию каждой массы по формуле, соответствующей движению конкретной массы (поступательное движение, вращение вокруг неподвижной оси, плоское движение и т. д.). Следует помнить, что кинетическая энергия является положительной величиной независимо от направления движения массы, поступающей в систему. Задача 334.Если P-вес колеса, а < vc-скорость его центра инерции, то вычисляют кинетическую энергию катящегося колеса, которое не скользит по прямому рельсу. Колесо считается непрерывным однородным диском. Решение. Поскольку колесо совершает плоское
движение, его кинетическую энергию можно рассчитать двумя способами по формуле. а)Т = Я МВ\: + — Б)Т = .j Где Igi-момент инерции твердого тела относительно оси через мгновенный центр скорости, перпендикулярный плоскости симметрии материала объекта. Цели 334 В связи с потоком оценки вычислительной сложности можно отдать предпочтение варианту Б).Однако, как показывают последующие расчеты, оба варианта имеют примерно одинаковый вычислительный вес. Вариант а): 10 ′ — /=МВ ^ р а, 2с Момент
инерции диска относительно оси z через центроид C перпендикулярен плоскости материала Пиар * Симметрия колеса заключается в следующем. f, c = » радиус колеса de обозначается через G. И так оно и есть.、 1П, 1 стр-、 7 = = РМ- — — О — > — <О. 2 вместе Если колесо не скользит и не катится, то мгновенный центр скорости находится в точке контакта oP колеса и рельса, поэтому vc = r <&и Уравнение кинетической энергии Га п г =-; 7; гг 4 г с Вариант в): ул Т = Дж БА = 2 бб * е Л — = и к = я И Меня («2а. г.) И я Где Fa> » Fkz-проекция главного вектора сил, действующих на A-ю точку
системы. Теорема о работе равнодействующей силы: работа равнодействующей силы, приложенной к точке определенного перемещения, равна сумме работы составляющих сил того же перемещения А (Р)= С А (П), где п =£ К — = Я LG » −1 — Момент инерции колеса относительно оси через центр скорости eP в момент, перпендикулярный плоскости симметрии материала колеса. Поскольку оси rc и & параллельны, то если применить теорему
штейпера, то получим: Теперь мы узнаем: Г1 О 1 3 р д л = 2&-2 «2 г в случае rm = vr, это, наконец, выглядит так: Задача 336.Груз а груза а опускается со скоростью, которая идет вниз по наклонной плоскости, а приводной барабан в груза Q наматывается вокруг it. Rope. To рассмотрим барабан — /-как однородный круглый цилиндр-Ji^ / * цилиндр. Масса веревки / / \ игнорировать. ^^(\?\ sigma-G » вычисляет кинетическую энергию W / системы и выражает ее с помощью скорости нагрузки \ ^ ^ J A.\ I ^ Y Решение.
Система*состоит из 2 масс. К задаче 335.Таким образом, кинетическая энергия системы равна нагрузке Y ’ (.) и сумме кинетической энергии барабана. 7 ’=: 7CH1)+ 7CHH(1) Кинетическая энергия поступательно движущегося груза, 1 рассчитывается по следующей формуле = — МВ * = я / ХL(2) Кинетическая энергия барабана, вращающегося вокруг неподвижной оси r, перпендикулярной плоскости фигуры, получается по следующему уравнению: 7 — < » = 4 / y, (3) Где 12-момент инерции барабана относительно оси вращения г, а W-угловая скорость вращения барабана. Думайте барабаны Поэтому
непрерывный равномерный круглый цилиндр Я = ° — Г-(4) Здесь радиус барабана обозначается r. подставляя значение Iz из Формулы (4) в Формулу (3), получаем: 7 *(9)= — LA Высота точки на ободе барабана равна скорости движения груза, она должна выглядеть так: v = rsh, следовательно、 7CH1)= * О Л(О) £ 4 в Подставляя значения 7 ’(1) и 7 (i) из формул (2) и (o), находим искомую кинетическую энергию системы. Задача 336.Рассчитайте кинетическую энергию механизма, показанного на рисунке. Колесо 2 с массой P и радиусом r、
Внутренняя шестерня с неподвижным колесом / радиусом R = \ R. колесо 2 приводится в движение массой Q OS кривошипа и имеет постоянную угловую скорость(00.Поверните колесо 2 вокруг неподвижной оси O, перпендикулярной плоскости рисунка, чтобы увидеть кривошип ОС в виде тонкой однородной формы Rod. It выражает кинетическую энергию с угловой скоростью. И про
кривошипа ОС. Решение. Рассматриваемая система включает в себя 3 массы колеса/, колесо 2 и кривошип. Таким образом, кинетическая энергия системы будет равна сумме кинетической энергии этих масс 7 = р(х) — ф Здесь 7 (|) — кинетическая энергия коленчатого вала ОС. Потому что колесо 1 неподвижно、 7 ^ = 0. Ноль) Семьсот сорок три)_ / Т <2> Колесо 2、 (2)
Колесо 2 совершает плоское движение. Его кинетическая энергия будет: = + я / с * 1(3) Длина кривошипа будет равна OS = = — = R-r = 2g. So … ВК = ОС — <о0 = 2r0. (4 )) Определить мгновенную угловую скорость колеса 2, учитывая, что точка aP является мгновенным центром скорости, то есть vc = rwit ВР У = г = 2sh0. (5) Потому что колесо 2 представляет собой ровный круглый диск、 При расчете
по формулам (3), (4), (5) и (6) получается кинетическая энергия колеса 2. Семь> = 3-J hC (7) Кривошип ОС вращается вокруг неподвижной оси O, которая перпендикулярна плоскости figure. So, его кинетическая энергия рассчитывается по формуле T ^ 1 == / 0 , следовательно、 ДГ о г г, ч)= / р гхг. (8) Формула(2)、(7)、(8)подставляя Формулу (1), находим искомую кинетическую энергию механизма. Задача 337.Рассчитайте кинетическую энергию
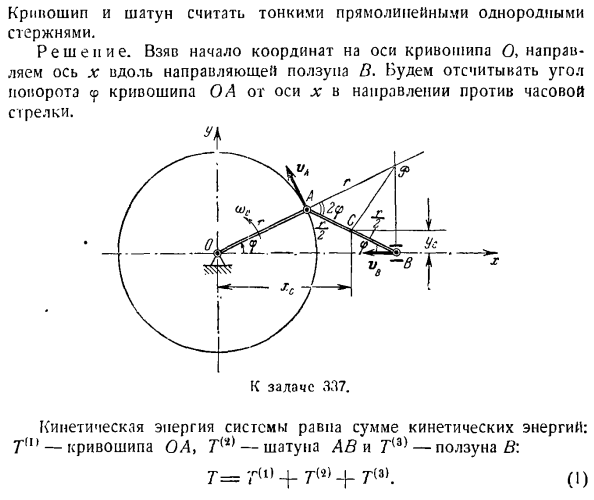
кривошипно-шатунного механизма, где масса и длина кривошипа ОА равны массе шатуна АВ соответственно.Кривошип OA с массой P и dtype r вращается с угловой скоростью ω0.Вес ползунка B равен Q. Тонкие и тонкие прямые однородные стержни, с учетом кривошипа и стержня. Решение.Укажите ось x вдоль направляющей ползунка B с осью кривошипа O в качестве начала координат.отсчитывает угол поворота (cp) коленчатого вала OA в направлении против часовой стрелки от оси X. Тс Кинетическая энергия системы будет равна сумме кинетической энергии: Tm-кривошип OA, T (>=.> 4 + 1 / s dry, где V-
основной вектор системы сил, а dr-фундаментальное смещение любой точки твердого тела. б)8л = м2д J + 2rV£s! NV(13) Подставляя формулы (B), (12), (8) и (13) в формулу, получим: Объем вычислений, необходимых для расчета кинетической энергии каждого дополнительного шатуна, примерно одинаков. Переходим к расчету кинетической энергии ползуна В.
Подставив Формулы (2), (11) и (16) в Формулу (1), получим искомую кинетическую энергию кривошипно-шатунного механизма. Задача 338.Выведите формулу для кинетической энергии твердого тела, вращающегося вокруг неподвижной точки, используя формулу для проекции скорости твердой точки на ось декартовых координат, связанных с твердым телом (формула Эйлера). Решение. Если начало координат O находится в неподвижной точке, а оси декартовых координат x, y, z связаны с твердым телом, то, как известно
из кинематики, формула Эйлера имеет следующий вид: ЧХ = іх)У2-iguu вы = ОМК-ВЗ = shhu — < & ХХ,(1) Где x, y, z-координаты точки твердого тела, а iax, — 2uyo,^у 2dm-2угсолгdmdm-2 < AYU^XY DM). (4) (M) я (At)) Потому что сумма 2 квадратов 2 координат точки определяет 2 квадрата расстояния от этой точки до 3-й оси、 ^(У2-J2l) ДМ = $ frxdm = / А^(х -Р1) ДМ = \ сек. ДМ = ий (А1) (А1) (А1) (АФ) $(Л-2 −1-У1) ДМ = \ ч} СД =(о) (М)(М)) Кроме того, по определению ^ УГ ДМ = Ивз,^ ZX в ДМ = іх,\ ху ДМ = IXY в. (6) Лаф) » (АФ> [м) Подставляя (5) и (6) значения Ix, Iyi \ 2, Ixy, Ixz> lyz в уравнение(4), получаем искомое
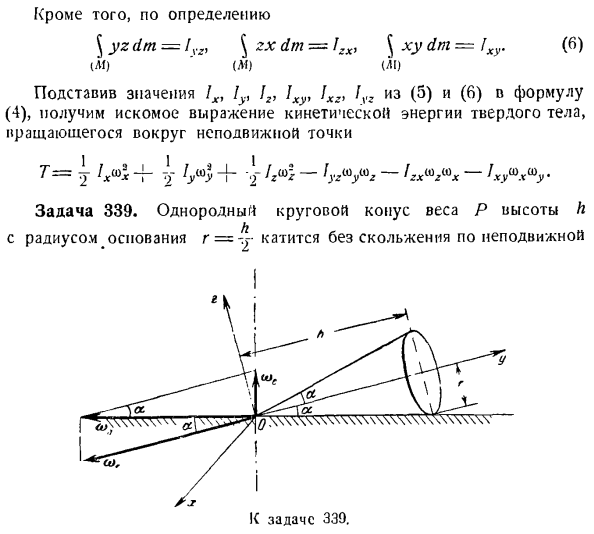
уравнение кинетической энергии твердого тела, вращающегося вокруг неподвижной точки Ти Джей! ХН—•)!Wow + 2 ″ — h’Z ^ fz — VW Задача 339.Однородный конус с грузом высотой основания радиусом r = — r, P, катится без скольжения по креплению В горизонтальной плоскости, вершина о неподвижной точке. Рассчитайте энергию движения конуса, когда он вращается вокруг вертикальной оси в течение 1 секунды до 1 секунды. Решение. Выберите начало координат осей x, y и z в фиксированной точке O. укажите ось y вдоль оси симметрии конуса. ось z расположена в вертикальной плоскости. Горизонтальная ось X перпендикулярна плоскости чертежа. Поскольку конус
вращается вокруг неподвижной точки O, оси x, y и z являются главной осью инерции конуса в точке O, поэтому lxz = l2x=. lxv = 0, то есть кинетическая энергия конуса рассчитывается по формуле М = 1 — (У * + 1.Г> + 1А). (О Где/ x, Jy, 1r-момент инерции конуса относительно соответствующих координатных осей, а » oh,©, ok-проекция мгновенной (абсолютной) угловой скорости конуса на соответствующие координатные оси. Момент инерции конуса/ l, Jv,/, найденный в задаче 291. \ В-10 О-Г «- — — Л Л — \ ’ Л• £ 10 » * 5£1,9 4 /
Конус, вращающийся вокруг неподвижной точки O, участвует в 2 вращениях вокруг пересекающейся оси (переносные вращения выполняются вокруг вертикальной оси, относительные вращения центрируются вокруг оси симметрии конуса у), а затем применяет теорему о сложении вращения твердого тела вокруг пересекающейся оси: o», — 1-o), создавая квадрорельс угловой скорости. Вектор момента (абсолютной) угловой скорости конуса находится на мгновенной оси, которая направлена горизонтально вдоль линии контакта между стороной конуса и неподвижной поверхностью.
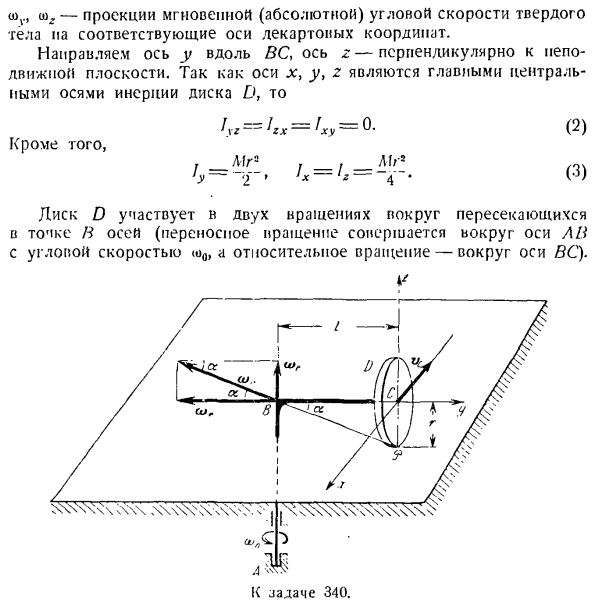
Легко увидеть, если угол вершины конуса равен 2a Что?! Юя= ги> ГС1 га. (3) вычислите проекцию ya на оси x, y и g. о) = — сода потому что, М.. = грех, а <АГ = 0«(4) (Параллелограмм угловой скорости находится в плоскости YZ). Используйте выражения (2), (3) и (4) для описания выражения (I) в виде: R = «7 <3 * 4 + t) cos» O. потому что… — , a, поэтому в соответствии с условиями задачи r = fj и Ых и ф г sect1, наконец, получить: 3 ″ П Л Проблема 340.Siobodopa на оси собачки P диска D и радиуса r, BC приводится в движение сломанным рычагом
LAN. Диск вращается без скольжения. Неподвижная горизонтальная плоскость. Кривошип ABC вращается вокруг вертикальной оси с угловой скоростью o) 0.Рассчитайте кинетическую энергию диска. Solution. In в общем случае движения твердого тела кинетическая энергия рассчитывается по формуле T = ^ mvt + — 2-f}боевые искусства » r W- −21 >>>•»>、-^ на ZX ^ х〜(*) Где M-масса твердого тела, а vc-скорость его центра тяжести C. 1X, y, 1g-момент инерции оси, 1xu, 1yu, 1xg-центробежный момент инерции твердого тела относительно оси, связанной с диском, начало которого отрегулировано на центр тяжести твердого тела.、
< OV, tnz-проекция мгновенной (абсолютной) угловой скорости твердого тела на соответствующую ось декартовых координат. Направьте ось y вдоль BC, а ось z перпендикулярна неподвижной плоскости. Оси Y, Z, чтобы быть центральной оси инерции диск D、 О. / _ Мг*, Афи * ’в ’О’ » х ’г’* (2) (3)) Также Диск D принимает участие в 2 вращениях вокруг осей, пересекающихся в точке B (переносные
вращения выполняются вокруг оси A B с угловой скоростью около 0,а относительные вращения-вокруг оси BC). а, л, с Что?! к джаджаку 340. Мгновенная ось r » (абсолютная ось вращения) перемещает череп в точку B через точку контакта диска с неподвижным диском на пересечении переносной оси вращения и относительной оси вращения. Применим теорему сложения к вращению твердого тела вокруг пересекающейся оси: ojrt = u) e-o) l, построив параллелограмм угловой скорости. Это и есть рассматриваемый прямоугольник. Представляющий угол рефлектора с легко найти Вт.==_ = -. 0.Сил
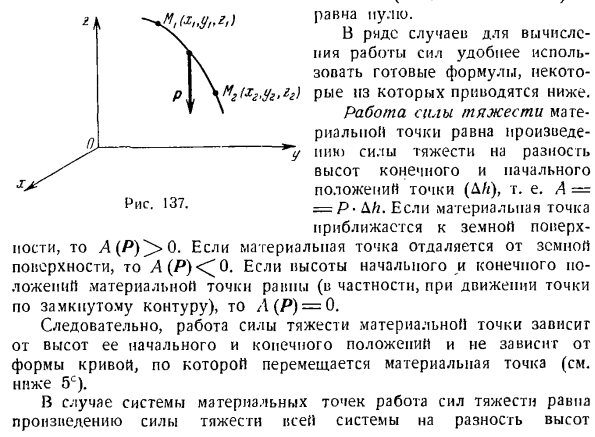
а Сингх. Треугольник от ВСФ г Грех я =- Г * * Й* ’ Равный нулю. В некоторых случаях удобнее использовать готовые формулы для расчета работы силы. Вот часть формулы (Mg (x1, y2, yr)): Гравитационная работа материальной точки равна гравитации (D/*) известной гравитационной точки, то есть A-= P•DL, для разности высот между конечным и начальным положением точки. Если материальная точка приближается к поверхности Земли, то это a (P)> 0.Если материальная точка находится вдали от поверхности Земли, то она равна A ®<0.Если высота начального и конечного положения
материальной точки равна (особенно если точка движется по замкнутому контуру), то D ®= 0. В результате работа гравитационной силы массы зависит от высоты ее начального и конечного положения и не зависит от формы кривой, по которой движется масса (см. 5E ниже). В случае системы материальных точек работа силы тяжести равна произведению разности между силой тяжести и высотой всей системы. М (х » уя、) Рисунок 137. И затем… «Ля»- если вы определяете XY y, проекцию o> a на ось z, т. е. wx, w, w, w, w, вы получаете: о > 0 в? «- {- Г2I Я о) г =-Ива соѕ а = ——- р = — (часто-、
г р г *.|. / Л О Г• = wx = 0(4) (Прямоугольник угловой скорости находится в плоскости d’r).Скорость точки С — это формула р «с = H0O0 == / В0. (Г) Формула(2)、(3)、(4)、(5)и используйте формулу (1), чтобы получить нужную формулу для кинетической энергии диска. м = я J(6 / я + ’*) Проблема 341.Куб массы M движется линейно со скоростью v вдоль горизонтальной плоскости, а ось математического маятника усиления O массы m с длиной винтовой резьбы / соединена с кубом. Рассчитайте кинетическую энергию
материальной системы, исходя из известного закона маятника: 9 = 9(0.(Вектор v находится в плоскости качания маятника.) Определение: поскольку рассматриваемая система состоит из куба и материальной точки A, искомая кинетическая энергия t равна Gamma=Gamma (|>+7hv), (1) к выпуску 341. Где 7 (.) — кинетическая энергия Куба, а T {i] — кинетическая энергия точки массы A. Потому что куб движется постепенно、 7 «(l> = 1 МВЛ. (2) Кинетическая
энергия точечной массы A Где<оа-абсолютная скорость точки А. точка а совершает сложные движения. Вместе с кубом вы можете перемещаться относительно Куба. То есть v£= v и vr = l%(где 9-угол поворота маятника). Примените теорему к сложению скоростей va = ve + vr, чтобы создать параллелограмм скорости (см. Рисунок).Используя косинусную теорему скоростного параллелограмма, можно увидеть следующее: в \ = в * + в * 4-27) в COS Ф Л Г И Г Е Г | если вы замените значение ve и VR, это выглядит так: в V \ = У3 + г + УФ-с COS <Р、 Для этого Р <*> = Я=} J т (м> * -ф / В-Ф 2 / $ р>
потому что(3) Введите значения(1) формул (2)и (3) до 7CH1)и 7 «t2), чтобы получить искомую кинетическую энергию системы. Т = ТЖ (ж + Т) уу + 2 «Ш ^ В + потому что Следует отметить, что кинетическая энергия этой системы зависит не только от скорости точки, но и от расположения точки системы(в пункте 3 имеется коэффициент cos®). Проблема 342. 3 упругие диски/, 2 и 3 прикреплены к упругому горизонтальному валу, и момент инерции к оси вала равен/|, / а и/ 3.As в результате упругости вала и его вращения диск вращается под разными углами. Знать
зависимость угла поворота диска, а также < Р3 против времени, вычислить кинетическую энергию системы. Масса вала игнорируется. Решение. Кинетическая энергия системы T равна сумме кинетической энергии трех дисков. Ф.— 7 * ( » ) 7×2) l_ Поскольку диск вращается вокруг неподвижной оси, следовательно, требуемая кинетическая энергия равна
Проблема 343.Рассчитайте кинетическую энергию системы, состоящей из груза и пружины, где груз массой W подвешен на однородной пружине массой m>вызывает свободную вибрацию. При расчете кинетической энергии пружины предположим, что смещение точки пружины пропорционально расстоянию от точки усиления О. Решение. Направьте ось s вдоль оси пружины и укажите точку отсчета точки подвешивания пружины к потолку. Поскольку рассматриваемая система состоит из нагрузки и пружины, ее кинетическая энергия равна ДУА. Т = Т1°+ Т4>, (1) Где T(1) — кинетическая энергия нагрузки, T (<1) — кинетическая энергия пружины. Да. Л Р? Смещение груза показано в x для описания его
кинетической энергии (2) Т(1)= 1 МХ Осталось рассчитать кинетическую энергию пружины. Введем следующие обозначения. I-длина недеформированной пружины, f-плотность пружины. Выберите длину пружинного элемента ds на расстоянии s. благодаря свободной вибрации системы все точки пружины и нагрузки перемешиваются. Смещение пружинного элемента ds, который отделен расстоянием s от точки усиления O, показано в i. в зависимости от состояния задачи смещение точек пружин пропорционально их расстоянию og ы ы ы Точки O, то есть, где
заработать; = y x. возьмем производную В К выпуску 343. * с К тому времени, как мы найдем:- Кинетическая энергия длины DX пружинных элементов dTKi) = dnfi? Здесь масса пружинного элемента равна dtn = * [ds, т. е. =(3) Принимая определенный интеграл в диапазоне от 0 до I, вся пружина получает кинетическую энергию. Я Потому что масса пружины равна M = 7 /、 Один — ТХ (4) Подставляя значения T (2) и T (1) и T (9) из уравнения (I) (4), получаем искомое уравнение кинетической энергии системы. Именно поэтому, приблизительно учитывая массу пружины, необходимо прибавить 3 минуты 1 массы пружины к массе груза (приближение Рэлея). 3 ’.Теорема об изменении кинетической энергии массы. Изменение
кинетической энергии при движении материальной точки равно сумме задач, выполняемых силами, приложенными к точкам этого движения. м » — м= А (Ф、)、 Один.— Я Или н — 2-МВЛ-2 МВ \ = 2 А(ФК). k = I Используя теорему об изменении кинетической энергии материальной точки, необходимо решить задачу в следующих случаях: масса m (или масса P), скорость движения точки, а также-в первый и последний момент напряжения, сила, приложенная к точке, движение точки. Задача может быть легко решена с помощью определенной силы и силы, соответствующей
расположению точки. В следующем порядке рекомендуется решить задачу, используя теорему об изменении кинетической энергии точек масс. 1) Установите усилие, приложенное к материальной точке, то есть силу и силу реакции муфты. 2) вычислить сумму работы всех сил, приложенных к точке массы, при движении. 3) вычислить кинетическую энергию массы в начальном и конечном положении. 4) используя результаты расчета предыдущих 2 пунктов, применяем теорему об изменении кинетической энергии точки масс и определяем искомое значение. Задача 344.Материальная точка, находящаяся на кривой траектории, которая через некоторое время замедляется и останавливается, а затем начинает двигаться
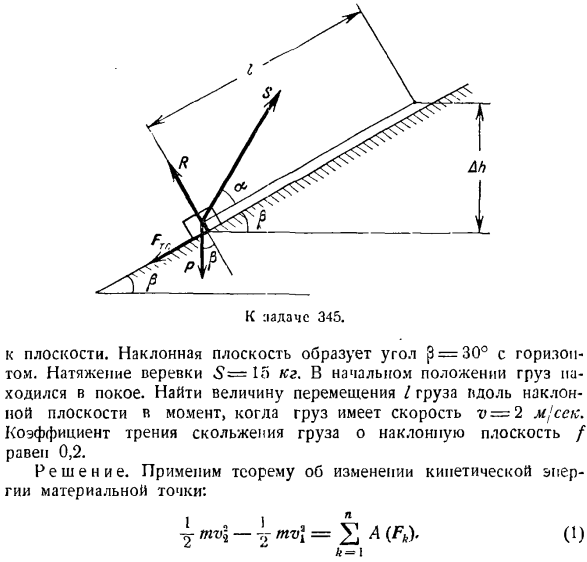
из стационарного состояния. Вычислить сумму сил, приложенных к точкам этого смещения. Решение. Применим теорему к изменению кинетической энергии точки масс. н 2 МВ -2 = 21 а ^ В начале и в конце движения материальной точки ее скорость равна нулю, то есть g. если = r » 9 = 0, то из Формулы (1) видно, что сумма работы всех сил, приложенных к массе соответствующих перемещений, равна нулю. £А (Кеннеди)= 0К = 1 Задача 345.Вес Р-20 кг поднимается по наклонной плоскости тросом с углом а = 30° Перейти к 345. В самолете. Наклон образует горизонт, а угол£} = 30°.Веревка напряжение » с = 1г> кг. В исходном положении, груз был остановлен. Найти величину перемещения / нагрузки вдоль наклонной плоскости в момент, когда скорость груза v = 2 м / ССК. Коэффициент трения
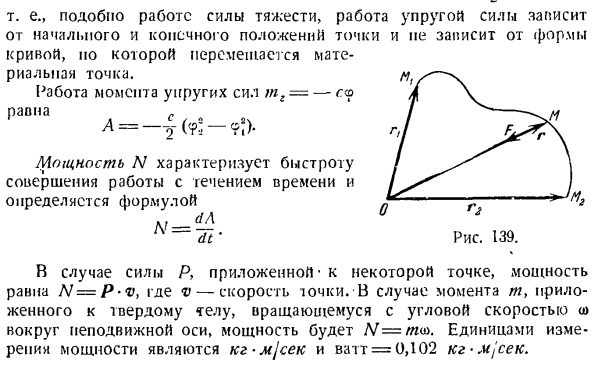
скольжения нагрузки на наклонную поверхность / вершину равен 0,2. Решение. Применим теорему к изменению кинетической энергии точки масс. 1 и я 2 mvl-7Гmvl = 2А0) Конечное и начальное положение центра инерции системы: н Где P = ^ Pk>и ось z ориентирована вертикально. Один Работа упругой силы= — cx для прямолинейного движения вдоль линии действия сил от точки абсциссы xx до точки абсциссы xb) (рис. 138) (если n * = 0, то сила упругости будет равна bullet. In другими словами, пружина не подвержена стрессу.) VWWWWW //// В/ 7 ///// В /- —— .Г、- Рисунок 138. Если точка движется в направлении увеличения коэффициента
упругой силы, то работа упругой силы отрицательна. Если точка движется p, то работа упругой силы положительна. Сторона, где модуль упругости уменьшается. Работа упругой силы F =cr при конечном перемещении по криволинейной траектории пропорциональна разности квадратов Начальный радиус печи и вектор точек: A = — O «
P-вес груза, S-сила реакции троса, нормальная сила реакции наклонной плоскости, Fr c-сила трения скольжения груза на наклонной плоскости, FTшС = FNT, нормальное давление N = PCOS P — ^ Sin a; следовательно, Plc = / (pcos P-5 Sin a). Вычислите сумму этих сил для движения грузов, равную/. ^ А(Ф)= А (П)+ А (Х)+ А (Х)+ А(Ф) (ФК. с.) (-2) поскольку I РУз поднимается, работа гравитации становится отрицательной: 4 (P)= — RAL = — PI sin *(3) Сила реакции веревки с это Л [Х) = сл потому что. (4 )) Поскольку сила R перпендикулярна смещению f, нормальная реактивная сила
на наклонной плоскости£работы равна нулю. Д(/?) =0.(5) Угол между силой Fr c и направлением перемещения/равен 180°, поэтому работа силы трения скольжения Fx c отрицательна. Л (ФК)= — фут. КЛ =- /(п сов?- ^грех)И.(6) (2) Формула(3)、(4)、(5)、а подставив значения A (P), A (5), A ®, A (FT c) из (6), можно увидеть сумму работы всех сил. Прикрепленный к грузу и двигающийся в I: Х (ФК)=число(потому что + / соз А) — Р(Син (3 + / соз Р))/.(7 )) Приступим к расчету изменения кинетической энергии load.
In в исходном положении груз был неподвижен, и поэтому 7 | =0.In конечная позиция, вы получаете нагрузку принять в бОльшего размера. То есть, 1 \ = 2-v- С Так Что 1 Р / О. Из формул(7)и(8)^ A (Fk)и T. подставим значение 2-T в уравнение (1), чтобы определить искомое смещение. / В ^(Потому что А-Ф / порожка) — П (Jiin ^ + / потому что Если присвоить числовые данные, то можно увидеть, что это/ = 3,54 м. Проблема 346.Груз массой P свободно колеблется с подвешенной к потолку пружиной, а коэффициент его упругости (жесткости) равен S. о нагрузке, находящейся в состоянии статического равновесия, сигнализировало воздействие скорости v0. Определите скорость движения груза v, зависящую от смещения из положения
статического равновесия и амплитуды колебаний груза. Решение. Применим теорему к изменению кинетической энергии массы:^.www » н −2 МВ \—J в МВ \ = г (ФК). Ноль) k = I ось x опускается вдоль оси пружины и выбирает положение статического равновесия нагрузки, то есть точку отсчета, когда пружина имеет статическое растяжение: = 4•(2) с Указывает нагрузку в положении, сдвинутом на x от начала координат. Установленный на грузе: P-вес груза, сила упругости F-пружина / D |.С момента расширения Величина пружины при определенном положении груза равна Я Я F меня Y Д = ДСТ + х, что FX = — с(ПКТ + ЛТ). И затем… Голы: 346 вычислите сумму сил, приложенных к грузу при перемещении, равную x. 2 А (ФК)= А (Р)+
А(Ф). (4 )) Функция силы тяжести при перемещении груза от нуля до x равна a (P)= Px. (5) Если нагрузка перемещается вниз от начала координат до x, пружина удлиняется, поэтому работа упругой силы F равна negative. In в начальном положении груза пружина деформируется на Дсг, а в конечном положении груза она смещается от опорной точки вниз на X: A= Act-J-JT (см. уравнение (3)).Следовательно, работа упругой силы равна A (F)= ==- ^(Да-ДС2Т).Используя формулу(3), получаем: A (F)=〜•(2DSTL + A ^(6)
Подставляя значения A (P) и A (F) из формул (4) (5) и (6), можно увидеть сумму сил, приложенных к нагрузке, когда нагрузка движется вниз от пули X. Λλ (Fk)= Px — (2 Dst * + x*). Формула(!2) Когда дано, это выглядит так:%А (Ф>)=-Е-£. (7 )) Затем рассчитайте изменение кинетической энергии load. In начальное положение, груз был уведомлен о скорости r » 0. Т-1 Р Т, 2 В конечном положении нагрузка приобрела скорость v、 2 а г Таким образом, изменение кинетической энергии нагрузки является Г, — Г,= 1 Л. (R-5). (8)
Подставив значения ДД и 7,» -, определим скорость движения груза по перемещению X из уравнений (1) (7) и (8). Как известно из теории колебаний материи точки〜= kr, где k-круговая частота колебаний точки load. So, в конце концов: в = ВВЛ~!ГХ (9) При отклонении нагрузки в крайнее положение x = zLa ее скорость исчезает, поэтому амплитуда свободного колебания нагрузки a легко определяется по формуле (9). Подставляя эти значения в уравнение (9), находим амплитуду свободной вибрации груза. 4°.Теорема об изменениях
кинетической энергии материальной точечной системы. Изменение кинетической энергии при движении системы материальных точек равно сумме работы всех внешних сил и внутренних сил системы на это движение. Это единственная из 4-х общих теорем динамики, и формулировка включает в себя не только внешние силы, но и внутренние силы. Наличие внутренних сил в формулировке теоремы несколько усложняет решение задачи. Однако при необходимости определения внутренних сил задача может быть решена с помощью теоремы общей динамики только при
применении теоремы к изменениям кинетической энергии материальной системы. В случае системы неизмененных материальных точек, например абсолютно твердого тела, сумма внутренних сил работы пули равна нулю, а теоремы об изменении кинетической энергии системы материальных точек нет.「
Теорема об изменении кинетической энергии материальной системы должна применяться тогда, когда искомыми данными и величиной являются: инерционные свойства системы (масса и момент инерции), скорость (линейная и угловая), сила и момент пары сил, перемещение(линейное и угловое). Задачи, в которых сила и момент пары сил постоянны или зависят от расположения точек системы, могут быть легко решены. решение теоремы об изменении кинетической энергии с помощью iiomouimo рекомендуется
проводить в следующем порядке: 1) внешние и внутренние силы системы показаны на рисунке pse (для немодифицированных материальных систем-только внешние силы). 2) вычислить сумму работы всех внешних и внутренних сил относительно смещения точек системы (для неизмененной материальной системы-только сумму работы внешних сил). 3) вычислить кинетическую энергию системы материальных точек в начальном и конечном положении системы. 4) опишите теорему об изменении кинетической энергии материальной точечной системы, используя результаты расчетов
пунктов 2) и 3). 7и-7,= 2 а (Фэк)+ Дж] а (Фи) Т ФК = я л Или в случае неизменных материальных систем: = С Л(К), К = −1 Определите желаемое значение. Задача 347.Агрегат машины работает под действием системы приложенных к нему сил. а) пуск, б) остановка, в) определение знака суммы работы этих сил при постоянном действии. Решение. Напишите теорему об изменении кинетической энергии материальной точки : н Т% — ч = 2 А(ФК). (1) Разделите все силы, приложенные к системе, на движущие силы (например, моменты,
создаваемые электроприводом). н ложное A (Fk dv) 0), и сопротивление (полезное футовый.*- Я Сопротивление: например, сила резания, когда резец удаляет наконечник из заготовки, сила штамповки и т. д., и сила вредного сопротивления: например, сила трения скольжения вала на подшипниковой обечайке, сила трения зубчатой передачи и др.)、 н Его работа отрицательна (V] A (Fk sopr)<^ 0).Напишите уравнение к » = 1 kie(1), учитывая эту классификацию сил: m * — Tx =ЛΛ (F*)) + 2Λ(Fk sop). (2) а) при приведении в действие узла станка скорость материальной точки, которая в исходном
положении равна нулю, равна increased. So,= 0, Tm = 0, но кинетическая энергия положительна. То есть изменение кинетической энергии системы составляет 1 \ — T \ ^ > 0,и из Формулы (2) мы видим следующее: фут = л = я Так как первая сумма положительна, а вторая сумма отрицательна, то при запуске модуль суммы работы движущей силы будет больше модуля суммы работы силы сопротивления. b)когда блок машины остановлен, скорость материальной точки в начальном положении(момент когда сила
повернута) То есть, как и в случае с работой гравитации, работа упругой силы зависит от начального и конечного положения точки, а не от формы кривой, на которой смешивается материальная точка. Момент упругой силы работы///,= — ger равен _ Л ’/ Л 2 \ Л = — 2-( 0、7 ^ = 0; таким образом, изменение кинетической энергии системы равно 1 \ <^ 0, и из Формулы (2) видно следующее: 2 A (Fk dv) — £Λ (Pk с p)<0. ФК = л=) Поскольку первая сумма положительна, а вторая сумма отрицательна, когда машина останавливается, модуль суммы работы движущей силы будет меньше модуля суммы работы силы сопротивления. в) в установившемся режиме работы скорость точки является периодической функцией. Например, период, в течение
которого вал двигателя совершает 1 оборот, 2 революций и т. д., т. е. T { $ ) = T($-{-2 воздух), где£= 1, 2y …n. получим начальное положение сращиваемых точек системы, соответственно угол поворота вала двигателя<p, а конечное-угол поворота — | — k = 2,…Н, ТДж(?) = с — J — ’ 2К-з).Таким образом, изменение кинетической энергии системы пуль будет равно: −7′, = 0 Н. Н. Н. A A(FkJ +ЛΛ (^ sopp)= 0. х- * В установившемся режиме работы станочного агрегата модуль суммы работы движущей силы будет равен модулю суммы работы сил
сопротивления при одинаковом угловом перемещении вала, поскольку первая сумма положительна, а вторая отрицательна (если период времени равен нулю).
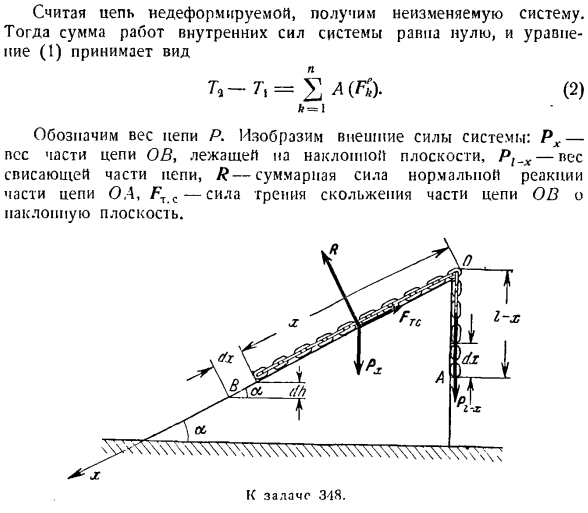
Задача 348.3 минуты 2 равномерного значения длины / AN лежит на наклонной поверхности призмы под углом I к горизонтальной плоскости, а 3 минуты 1 цепь висит вдоль вертикальной поверхности призмы(см. Рисунок).Под действием своего веса Хо, который был неподвижен в первый момент, начинает скользить вниз по наклонной плоскости. Определите скорость цепи в момент, когда конец подвешенной части а поднимается до точки О на наклонной плоскости. / — Коэффициент трения скольжения цепи по наклонной поверхности. Решение. направим ось x вниз от точки O вдоль
наклонной плоскости. Давайте нарисуем цепь во время движения. Он представляет собой OH с x, затем OA-I-x. напишите теорему об изменении кинетической энергии материальной точечной системы −7 = В А (Х.) В (Интернет). к-1 ч = я Если принять во внимание, что цепь недеформируема, то получим инвариант system. In в этом случае сумма внутренних сил системы сводится к нулю, и уравнение (1) принимает вид: (2) Показывает вес цепи P. давайте покажем
внешнюю силу системы: Px-вес части цепи OVL на наклонной плоскости, вес части цепи висит, R-общая вертикальная реактивная сила части цепи 0.4 Ft s-сила трения скольжения части цепи OB на наклонной плоскости. Дадим ворсу цепи B основное смещение dx вдоль наклонного вниз plane. In в этом случае конец цепи a поднимается выше dx. Рассчитайте основную работу внешней силы относительно движения dx 8.4 => 2 8.А (м)= 8А (ПКС)+ 8.4(/>、、)+ 8 а(/?+ 8 А (ГТ. с.) (3) вперед РХ = Ил:, футов. С = /Λ/ = / РХ соѕ а = / £л; с
оѕ а=; (/- р М = /> х < / / / = грех = З-й грех а л: Ар (4) А (/>, .)= — Пи-х ^ х = ДХ>(5) М(я)= гексогена потерь j = 0,(6) 8 л (/МК)= — центр ЦДХ—ф-л потому что xdx, (7) (4), (5) к bA (PX), bA (/?M (J. T.) C) подставим значение、 Из (3) формулы (6) и (7) видно, что: БА = 2 Вт (фо = Дж(л-грех-fcosa) xdx-ОПД(8) Для вычисления суммы работы внешних сил при перемещении цепи, при подъеме конца цепи а в Положение о, используют формулу, описанную в формуле (8) м Два 3 — / к /(начальный момент наклонной плоскости) Два Часть цепочки равна 0 /?= ;;-/В последний момент 「」 Скос должен быть по всей цепи. То есть, когда точки А и о объединяются, они должны
соответствовать равенству 0/3=/). Вычислив некоторый Интеграл, находим сумму работы всех внешних сил для некоторого конечного перемещения цепи. 2 A (K)= {J [5 (sin a — / cos a) −1). (9 )) Приступаем к расчету цепочки киззек energy. At в первый момент цепь остановилась. р= о. (Т) В последний момент все материальные точки цепи (с учетом их деформируемости) имеют желаемую скорость v, и поэтому、 7, = XV. (11) Значения^ A (Z^), Г и выражения(9)、(10)、(11)если подставить выражение (2) и решить это
выражение относительно v>, то получим: р «= м, — V&я ^(грех а — / соз а) −11. Движение цепи по наклонной плоскости возможно только при следующих условиях: о (грехе а-/ соз а) −1 0 или Подробнее о J \ COS A Проблема 349.Решите задачу 298, используя теорему об изменении кинетической энергии материальной точечной системы. Решение. Эта задача решалась с помощью дифференциального уравнения для вращения твердого тела вокруг неподвижного axis. In в этом случае необходимо было интегрировать дифференциальное уравнение
2 раза. Определите вращение кольца, 2 интегральные константы и вычислите время вращения, пока кольцо не остановится. Применение теоремы изменения кинетической энергии 7, — 7 -,= ^ А ^ П + С −4 (фи) 0) ФК = 1 К = Л Сумма расчета может быть уменьшена в несколько раз. На ней изображены все внешние силы и рассчитан момент инерции кольца Относительная величина к оси вращения r: 12 = ^(R * r1) и главный момент внешней силы относительно этой же оси: tag = — / Pr, как это было сделано при решении задачи 298,
суммируются н Работа всех внешних сил системы^ A (F%)= tag A ! (/**+Р2)<(р * р 4’2) л Du = 4 / gr-болезнь 77-Hn / gr-революция. Оказывается, с помощью теоремы об изменении кинетической энергии задача решалась достаточно просто, поскольку необходимо было получить зависимость между угловой скоростью (равной нулю при остановке) и углом поворота кольца. Либо=тогда вы должны решить дифференциальное уравнение.
Проблема 350.U = 72 км по дороге, пока автомобиль не остановится на прямом пути, в тот момент, когда вы выключите двигатель! Если бы вы двигались со скоростью света. Вес автомобиля, на котором ездят водитель и попутчик, равен P,= 1000 кг, а вес 4 колес равен pci = z 20 кг соответственно. Радиус инерции колеса относительно оси через центр инерции, перпендикулярный плоскости симметрии
материала, равен p = 20 см, а радиус колеса равен r = 25 см. Коэффициент трения колес, катящихся по трассе, равен/ к = 0,1 см. Игнорируйте силу сопротивления воздуха. Решение. При движении автомобиля вправо направление положительного ориентира для угла поворота колеса выбирается по часовой стрелке. Напишите теорему об изменении кинетической энергии материальной точки : (О 7-7 -,= 2 А (Ф> К)+ ^ А (/ = * <). Я * = 1 Вопрос 3 до 30. Указывает внешнюю силу, приложенную к автомобилю( см. Рисунок): Pi и 4Pq-сила тяжести,
2i и 2R » — вертикальная реактивная сила, которая смешивается против центра тяжести колес в направлении движения по значениям коэффициента трения качения/ k, 2Fp и 2f2TP. Do не изображайте внутренние силы, рассматривая автомобиль как неизменную систему и игнорируя внутренние силы friction. As в результате сумма работы всех внутренних сил системы равна нулю. Уравнение (1) принимает вид: М * — Т= 2 а (/«). (2) ■ И — = » Я Сумма всех внешних сил системы при требуемом перемещении 5 2 L (/ * ) = A (Ru) 4-4 A (PJ + 4 L(FTP)+ 4 A ( «» ) (3) k = I (Коэффициент » 4>соответствует числу колес автомобиля)». Вычисление суммы работы сил, приложенных
к системе масс или массовых точек, является одним из этапов решения задачи, где применяется теорема изменения кинетической энергии или составляется уравнение Лагранжа типа 2(см. главу X,§b ниже). Расчет суммы сил работы следует проводить в следующем порядке: 1) Нарисуйте силу, приложенную к системе материальной точки или материальной точки На рисунке; 2) показать основное движение точек в системе. 3) вычислить основную работу сил-сумму работы всех сил по основному перемещению точек в системе. 4)
вычислить искомую сумму работы сил от конечных перемещений как сумму определенных интегралов, взятых в соответствующих пределах основной работы, рассчитанной в предыдущем пункте. При наличии гравитационных и упругих сил можно рассчитать работу этих сил с конечными перемещениями по приведенной выше формуле, минуя последние 3 точки и выбрав систему координат. Проблема 328.Когда математический маятник движется, начальное положение нити образует вертикальную линию и угол, а в конечном
положении угол > < Пи). Если P-величина этой точечной массы и / — длина резьбы, вычислите сумму рабочих сил, приложенных к точечной массе маятника при этом угловом смещении. Направление положительное! Опорный угол поворота (cp) показан на рисунке. К выпуску 328. Так как разность высот Dh при смещении точек силы P и 4P2 равна нулю、 А (/>)= 4А(/> )= 0 (4) Если колесо вращается без скольжения, то центр скорости в этот момент находится на контактах. Сила трения всегда добавляется к колесу в точке, которая совпадает с мгновенным числом Центра скорости и движется вместе с ними. Сила этих сил трения, рассчитанная
по формуле/ V = Fyp-vcjf, равна нулю, так как Vcp = 0.Таким образом, работа силы трения при конечном перемещении, равная временному интегралу силы r, также будет равна нулю. 4Л(^ Мп)=0.(5) Учитывая, что радиус колеса и коэффициент трения качения одинаковы на всех 4 колесах, расчет суммы трения качения работает на 1 колесе, предполагая нормальное давление jV = P,+ 4Pj. Поскольку коэффициент трения качения/ k является плечом пары трения качения, момент пары трения качения будет равен / fr k = NfK =(P,-b
4PJU. Основная работа пары трения завальцовки 4ZL(я! Без надобности)= — mrtl д> Я =-(Р, — Ф 4П*) / К Д-Я (6) (Работа отрицательна, так как направление момента пары трения качения противоположно направлению угла поворота < p колеса), где dy-фундаментальное угловое смещение колеса вокруг мгновенного центра скорости. дс Если вы присваиваете значение < / < p выражения (7) (6): 4LA (ТИК)= — ( / > , + 4PJ для ds.(8) Для того чтобы рассчитать суммарную работу пары качения грепье при конечном смещении
центра тяжести С колеса, необходимо взять определенный интеграл диапазона, рассчитанный по формуле 8 (6.4), из Формулы 0: 4 а (дБ)=—(п, ч-4A2) а-.9. (9 )) (3) Формулы (4), (5) и (9) из A (P.), 4 A(P. 2), подставляя значения 4A (f7p), 4A (/nTtK), вы узнаете сумму всех внешних рабочих сил, приложенных к транспортному средству и его движению, равную S.: В А(Ф;-)=-(/>、+4 />、/ *&(10)
Приступим к расчету кинетической энергии автомобиля в первом и последнем случае position. In конечное положение, то есть время остановки, потому что скорость всех точек пули равна、 7 * =0.(11) Кинетическая энергия t {описывает кинетическую энергию автомобиля, состоящего из 5 масс: кузова с водителями и пассажирами и 4 колес、 ТХ = Т [{)-[-4(12) Кузов, в котором находятся водитель и пассажир, совершать постепенное движение、 Ту » = 4(13) Колесо для того чтобы сделать плоское движение、 v(v-v, J0 = P-p2, w = y, поэтому формула (14) имеет вид 47№= 2 +(15) О’ \ / Введение 値 値’) и 4г} 2) (12) уравнение I-H (13)и (15) указывают кинетическую энергию автомобиля в исходном положении. 7,= Г | П、+> +£)]•(16) Формула(10)、(11)、(16)если мы подставим
символы A (F), ’ Г2, Г в уравнение (2) и решим это уравнение относительно s,、 О, 1. г ч г г — ’ я [p,+ 4P2 {1 + — =53,4 м. 4У . + 4Pa) Проблема 351.Катушки веса P и радиуса r затем ослабляются и приводятся в движение резьбой, расположенной под углом a относительно горизонтали. К нити накала прикладывается постоянная сила F, определяющая скорость центра инерции катушки C в момент, когда катушка C перемещается на расстояние. Самолет.
Катушка не скользит и не катится. Масса нити игнорируется. g-радиус оси катушки, которая намотана на drink. At в первый момент система находилась в стационарном состоянии. Решение. Катушка сделает плоское движение. Мгновенный центр скорости, потому что завальцовка происходит без смещать Находится в точке соприкосновения с горизонтальной поверхностью обода катушки. давайте переместим ось s горизонтально вправо. возьмите
положительный уголпри касании as учитывается уравнение (2) 、 ^ ГК = ФСИН а) / к у. (5) Сила трения Fjpy, как и предыдущая задача, не выполняет эту работу. Конечно. ZA (FTV)= Frf-Vpdt = 0(6) (При прокатке без скольжения Сила F остается для расчета основной работы. После выбора точки CS запишите LA (F)= F-ds + mcd ®c= V (Г1rcosа〜 — F-ma) / к1 ′ °2) Из уравнения (12) видно, что катушка движется, когда коэффициент мощности Z7 удовлетворяет условию. ми&_ г, ф, г, потому что а-дж, дж, дж, порожка
кинетическую энергию автомобиля в исходном положении. 7,= Г | П、+> +£)]•(16) Формула(10)、(11)、(16)если мы подставим символы A (F), ’ Г2, Г в уравнение (2) и решим это уравнение относительно s,、 О, 1. г ч г г — ’ я [p,+ 4P2 {1 + — =53,4 м. 4У . + 4Pa) Проблема 351.Катушки веса P и радиуса r затем ослабляются и приводятся в движение резьбой, расположенной под углом
a относительно горизонтали. К нити накала прикладывается постоянная сила F, определяющая скорость центра инерции катушки C в момент, когда катушка C перемещается на расстояние. Самолет. Катушка не скользит и не катится. Масса нити игнорируется. g-радиус оси катушки, которая намотана на drink. At в первый момент система находилась в стационарном состоянии. Решение. Катушка сделает плоское движение. Мгновенный центр скорости, потому что
завальцовка происходит без смещать Находится в точке соприкосновения с горизонтальной поверхностью обода катушки. давайте переместим ось s горизонтально вправо. возьмите положительный уголпри касании as учитывается уравнение (2) 、 ^ ГК = ФСИН а) / к у. (5) Сила трения Fjpy, как и предыдущая задача, не выполняет эту работу. Конечно. ZA (FTV)= Frf-Vpdt = 0(6) (При
прокатке без скольжения Сила F остается для расчета основной работы. После выбора точки CS запишите LA (F)= F-ds + mcd ®c= V (Г1rcosа〜 — F-ma) / к1 ′ °2) Из уравнения (12) видно, что катушка движется, когда коэффициент мощности Z7 удовлетворяет условию. ми&_ г, ф, г, потому что а-дж, дж, дж, порожка
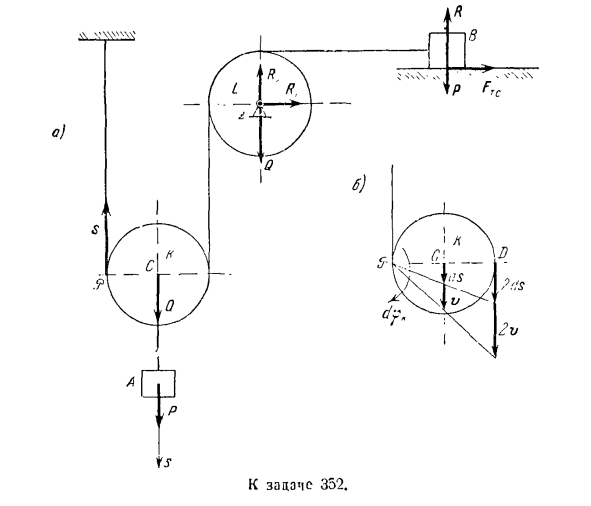
Задача 352.Нагрузки а и в устанавливаются во время работы 2 блоками подвижного К и неподвижного/. (См. рисунок а). в результате удара, нанесенного грузу L, груз начал снижаться со скоростью Pa. Нагрузка L и нагрузка I имеют одинаковый вес. Блоки K и/считаются однородными круговыми дисками одинаковой массы Q. коэффициент трения скольжения нагрузки B на горизонтальной плоскости равен/.Вес веревки игнорируется. 。 Решение. Ось s направляет центр инерции C движущегося блока K
вертикально вниз. угол поворота блока K по часовой стрелке и направление вращения блока L против часовой стрелки считаются положительными, соответствующими направлению оси s. Радиус блока обозначается буквой G. Напишите теорему об изменении кинетической энергии материальной точки : н (1) Поскольку Канат, охватывающий блоки K и L и руну B для привода, не деформируется, рассматриваемая материальная система, поскольку система находится в состоянии напряжения даже при
движении н Решение. 2. Сила приложена к точечной массе маятника. Масса Р и сила реакции резьбы R. таким образом, искомая сумма силовой работы равна、 л Ган = а (П)+ А(Р). 。 Ноль) к = 1 Так какова же сила реакции нити? Работа реактивной силы нити равна пуле, которая перпендикулярна основному перемещению dr, которое направлено вдоль нити и направлено по касательной траектории в этой точке при движении маятника.: А (Р)=0.(2) Гравитация P отрицательна, потому что точечная масса маятника поднимается. А (Р)= — РДЛ. Разница в росте копейка Это так immutable. As в результате сумма внутренних сил системы p () перестает
работать. Таким образом, выражение (1) принимает вид: B-7, = = £ЛW Поясним внешнюю силу системы: нагрузка A и B и блок K и L гравитация, R-нормальная сила реакции горизонтальной плоскости, FTX-сила трения скольжения груза B по горизонтальной плоскости, Rx и R * — сила реакции оси блока L, S-сила реакции каната. Дает фундаментальное смещение ds в вертикальном направлении вниз к центру инерции C блока K. In в этом случае блок K получает квадратное движение по часовой стрелке. Учитывая, что блок K, который совершает плоское движение, имеет мгновенной скорости центра АФ в точке контакта между блоком обода и левой ветви
каната, мы видим, что смещение обода в точке D равна 2дс (см. рис. Б).Как следствие, основное движение нагрузки Б выравнивается по левому краю по горизонтали, равна 2дс и углового движения блока L против часовой стрелки. Вычислим основную работу всех внешних сил системы: bL =£bA(f *) = bA (pa)+ 8a (q *) + ba (ql)+ ba (pb)+ + 8 А (Р)+ 8А(Ы)+(а)+ 8а(/ 4)+ ля(ФТ. С.) (3) Мы это выясним: =(4) =(5) = 0(б) (Точка приложения веса Ql фиксирована)、 BA (P0)= 0 (7) (Загрузить смесь B по горизонтали) * A (S)= 0 (8) (Сила реакции
веревки всегда приложена к мгновенному центру скоростей с)、 М(/?)= 0(9) (Нормальная реактивная сила R перпендикулярна основному движению груза B)、 8 A (Rx)= M (Ri)= 0 (10) (На R4 является стационарным с точки сила применения)、 Р # с)=- Форекс. cdrlv Движение груза dr8 по направлению к грузу равно 2ds, поэтому PIC = fP、 ба (включении компьютера)=-2 / П ДС. (И) Уравнение (3) в уравнении (4), (b)、(6)、(7)、(8)、(9)、
(10)и если вы замените(11)、 БА = в} М(Фдж)= [м — {- р(1-2/)] ДС. (12) Для вычисления величины работы искомого перемещения груза A, которая равна s, используя формулу (12), необходимо взять определенный интеграл в диапазоне от 0 до s. тогда существуют следующие условия: 2 ″ а » (ФП = [М + П (-2 / НС.(13 ))
Приступим к расчету кинетической энергии системы, которая включает в себя 2 нагрузки и массу 2 блоков. Мы пишем: T = TA T0 + Tk + TL. (14) Скорость груза A обозначается через V. Тогда vc = v. учитывая, что мгновенный центр скорости блока K находится в точке, получим vn = c2v(см. Рисунок B).Поскольку трос не может быть натянут, скорость груза B равна скорости точки D. То есть vn = 2v. ИС В Блок мгновенной угловой скорости K ’. г — = г, Угол ВД 2В Блок
L скорость:=- = — — (блок скорость обода пункт Б), которая равна ставке фрахта. Загрузите A и B, чтобы двигаться вперед、 7a = 2 (15) (16) Блок K выполняет плоское движение. ТК-младший в MVC + г Йк ва -> Где M = Q, Ic = — и поэтому (17 )) 7В -. 4G Блок L вращается вокруг неподвижной оси. TL = — y!/ * 1, где> t0 /.= = =. f ’ следовательно、 Да.*) Формула(15)、(16)、(17)、подставляя (18) и (14) в формулу, вы увидите кинетическую энергию системы. Р = Дж(10П — | — 7В). (19) В соответствии с состоянием проблема, скорость загрузки
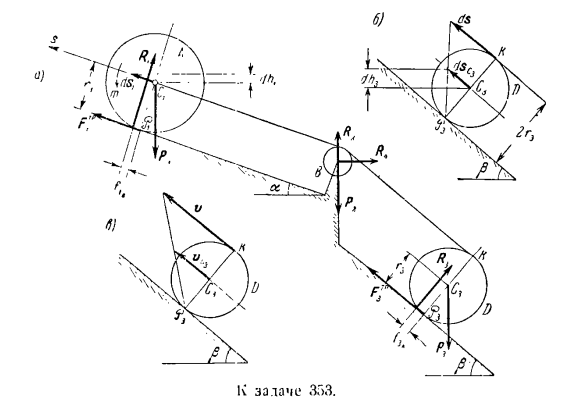
в начальное положение системы vQi. 7. = 2 (io / — b7Q). (20 )) В конечном положении системы скорость нагрузки а увеличивается в 2 раза、 Ви? Р4 =£(10р-я-7В). (21) 。Присвойте формулы (13), (20) и (21) Формуле (2) и решите эту формулу относительно s для определения требуемого перемещения груза A. Задача 353.Ось C К / вес Pt и радиус GX ролика a-это вес P. It перебрасывается через блок в 2 и привязывается к концу равномерного деформируемого троса, намотанного на цилиндр D массой P3 и радиусом g3. (См. диаграмму
а).Под действием крутящего момента, пропорционального углу поворота ролика, m = a <p, где A-постоянная величина, а ролик a поднимается по наклонной плоскости, которая находится под углом a к горизонтали, катится без скольжения, приводя цилиндр D в движение по канату. Сверните наклонную плоскость, которая находится под углом р к горизонтальной плоскости, не скользя.
Коэффициент трения качения ролика A вокруг наклонной плоскости равен/ 1k, а коэффициент ползучести качения цилиндра D с канатом, обернутым вокруг наклонной плоскости, равен/; k. Определите скорость вращения оси C{ролика A в положении системы, где ось Ci движется параллельно линии максимального градиента
Смотрите также:
Предмет теоретическая механика

