


- Мы определили силу сопротивления, используя формулу баланса импульса. Выпуск 5. 3 служит обзором применения этой формулы к протекающим вещам в пограничном слое. При применении формулы сохранения в интегральном виде необходимо знать распределение скоростей. Распределение скоростей турбулентного пограничного слоя представлено в разделе 12 для ламинарного пограничного слоя. Поэтому для определения сопротивления в турбулентном потоке вокруг плоской пластины мы используем интегральное уравнение импульса с профилем скорости, имеющим заданную разумную форму.
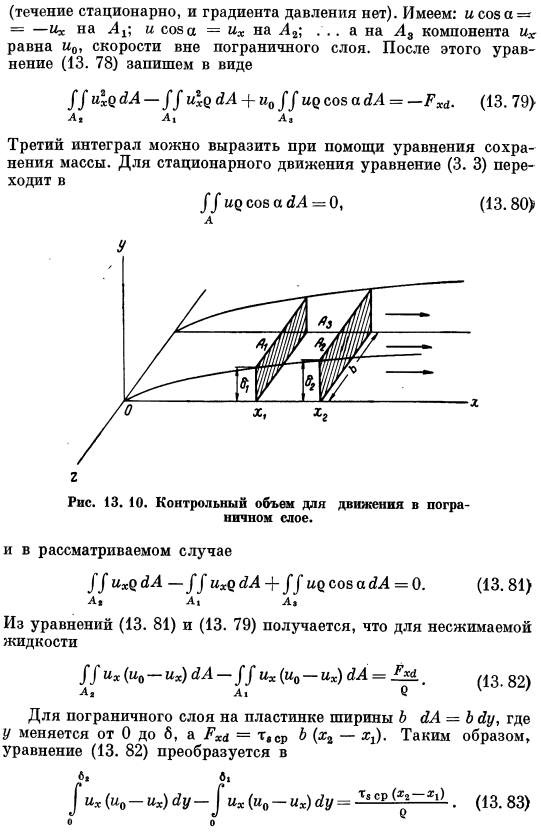
Этот метод основан на исследовании кармана и был использован полгаузеном при течении в пограничном слое при наличии градиента давления[125]. Применение ряда уравнений баланса движения к пограничному слою на плоской пластине Уравнение равновесия импульса должно быть применено к управляющему объему, показанному на рисунке. 13. 10.Поток происходит только на поверхности, указанной через Lp L2 и A3.Формула (5. 3) описать баланс х-составляющей импульса в виде: УУ 0 Цхи соз да — ФЛ а 13.
Семьдесят восемь. (Поток является стационарным и нет градиента давления).И cos a — = — в Lx; и те из cosa = L2. …А в A3 их составляющая равна u0, скорости вне пограничного слоя. Тогда формула(13. 78) в виде: // Пхе Ла 4 — М0 Tsitz потому что ЛА-и = — ГСГ. (13. Семьдесят девять} ЛЯ» 3-й Интеграл может быть выражен с помощью сохранения массы equation. In случай стационарного движения, уравнение(3. 3) выглядит так: UUyesozayl = 0, (13.80} Один 13. 10.Управляет объемом движения в пределах пограничного слоя. Если на стадии рассмотрения Г / MxO Ил-ый б / л + ый ИК сөз я =0.(13. Восемьдесят один) А » А » А » А » Уравнение (13. 81) и 13.
- Ислучаев несжимаемой жидкости. Ю их(ч0-их) (1А-ый их(ц0-их) (1А = 1×4 А > А1 0 (13.82). Для пограничного слоя на пластине с шириной b, ДА = B (1Y, y изменяется от 0 до G, px ^ = tacp B (xr-x^).Следовательно, формула(13. 82) преобразуется следующим образом: Его вода(x2-d1) О 。 (13.83) Учитывая распределение скоростей, можно вычислить Интеграл и найти тангенциальное напряжение m. однако это среднее напряжение за интервал x2-x±, и желательно знать значение m в этом отношении.
Это значение может быть представлено градиентом скорости заданного отношения х. (13.84) Таким образом, уравнение с использованием определения производной(13. 83) (заметим, что каждый определенный интеграл является функцией только x). (13. Восемьдесят пять) Как это О (13. Восемьдесят шесть) Формула (13.
Смотрите также:
