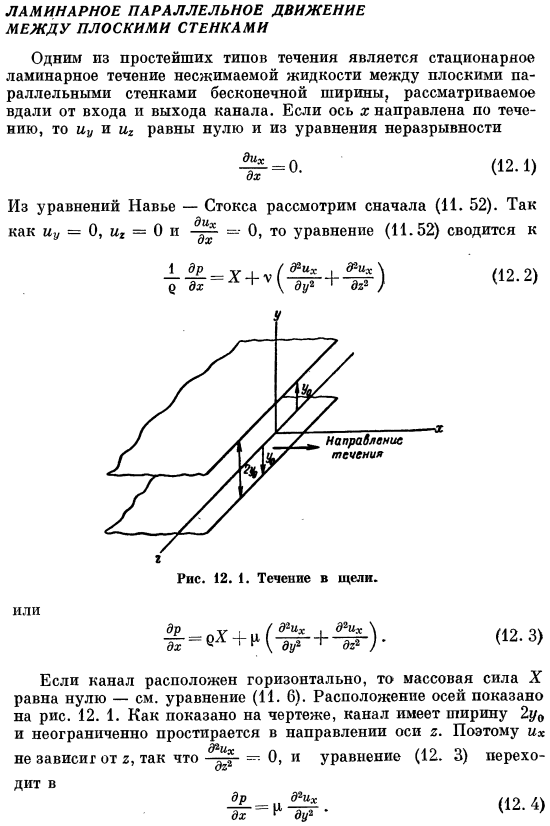



- Одним из простейших видов течения является устойчивый ламинарный поток несжимаемой жидкости между плоской параллельной стенкой бесконечной ширины, удаленной от входа и выхода канала. Если ось x направлена вниз по течению, uj и u2 равны нулю из уравнения неразрывности > = 0 — (12.1). Из уравнения Навье-Стокса мы сначала рассмотрим(I. 52). поскольку uy = 0, ui = 0 и-•0, выражение (11.52) выглядит следующим образом: Или Доктор ДХ. (12.2) д2иж 1 дхих \ 1 гр *) (12.3). Если канал горизонтальный, то массовая сила X будет равна нулю-формула (11. 6) см. Положение оси показано на рисунке. 12.
Как показано на рисунке, ширина канала равна 2y0 и неограниченно расширяется в направлении оси 2.So, так как он не зависит от r, то будет равен 0, а выражение(12. 3) быть н д * ДХ* ’ (12. 4) Затем мы кратко рассмотрим другие 2 уравнения Навье-Стокса. Формула (I. 54), поскольку все члены, включая u и массовую силу 7, равны нулю= 0.Если предположить, что ширина канала 2y0-мала, то вертикальная составляющая массовой силы Y также пренебрежимо мала, и Формула(11. 53)=0.Поэтому p не зависит от y и r и может быть записано вместо этого. Поэтому они являются в зависимости от x, во всех точках канала, удовлетворяющих сформулированным условиям, можно утверждать, что производная является constant.
Дифференциальное уравнение, подлежащее решению, после всего упрощения будет иметь вид: И их du2 1 Ар Р А S0P31. (12.5) Полное давление по вышеприведенным уравнениям для движения в зазоре можно рассматривать как сумму гидростатического давления (давления, существующего при отсутствии движения) и величины, называемой динамической Pressure. In практика, это динамический градиент давления, который вызывает movement. In в неподвижной жидкости полный градиент давления совпадает с гидростатическим градиентом, а динамический градиент давления равен нулю.
- Подставляя приведенное выше определение полного давления в уравнение Навье-Стокса, можно видеть, что полное давление заменяется динамической P ^массовой силой, а все остальные члены остаются неизменными. Следовательно, и строго равно нулю、 В неводном зазоре уравнение d2ih _ 1 Ард Au2 Р А (12. 6. Первые проведенные исследования привели к уравнению, которое не совсем точно, так как полное давление в нижней части канала несколько выше, чем в верхней части. Однако в случае динамического давления наклон в направлении оси y отсутствует, и Формула (12.6) имеет вид accurate. In многие книги по механике жидкости, уравнение Навье-Стокса написано динамическим давлением. Уравнение 12.
Интегралы Ди __ 1 Ар до-р а у ’ (12.7) если y = 0, то интегральная константа равна нулю = 0 (для удобства записи скорость и индекс опущены). В результате 2-го укрупнения (потому что если y = y0, то u = 0). — |- 0 и Y2 это уравнение обычно записывается в виде: Максимальная скорость itach достигается при y = 0.So выражение (12.9) может быть записано по-другому. — Sh ’ 1-(, 2L0) Из этой формулы и формулы баланса массы он получается таким же образом, как и в некоторых примерах ч. Три ____.3 часа? Б (12.11)г * о Приведенная выше зависимость может быть получена путем рассмотрения равновесия жидких элементов, выбранных для использования симметрии потока.
Смотрите также:
| Нормальные напряжения | Ламинарное движение в круглой трубе |
| Уравнения Навье — Стокса | Ламинарное движение в кольцевом зазоре |
