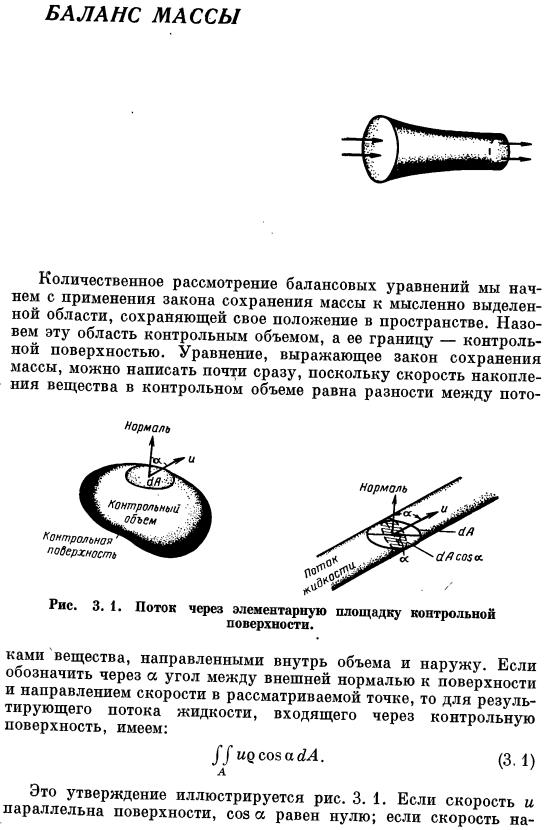






- Начиная количественное исследование уравнения баланса, применяя закон сохранения массы к мысленно различным областям, которые удерживают свои позиции в пространстве. Назовите эти области с управляющими объемами и границы с управляющими поверхностями. Уравнение для закона сохранения массы Равно разнице в управляющем объеме Нормальный. Рисунок 3. 1.Подача через низкопробное место поверхности управления. Вещества, которые направлены внутрь и наружу. Угол между внешней нормалью к поверхности и направлением скорости в рассматриваемой точке、 Результирующий поток жидкости с поверхности управления выглядит следующим образом: 1 d Дирсозабм.
Предложение показано на рисунке. 3. 1.Если скорость параллельна поверхности, то cos a равно нулю. Если скорость направлена в объем, то далее — ^ — и cos a отрицательны. На основе Из этого следует, что интеграл всей поверхности(3. 1) Вы можете проверить, что вы фактически представляете массовый расход результата от контрольного объема. Величина ri называется плотностью магнитного потока Измеряется по массе и кг / с-м2.Также известный как массовая скорость 10. кг! Интеграл с размерами Sec(3. 1)должна быть равна единице, взятой в противоположном знаке скорости накопления массы в контрольном объеме. Это утверждение применимо к любому импульсу.
Время, в том числе и зыбкое processes. In в общем, плотность варьируется от точки к точке, поэтому опишите общий коэффициент хранения массы в следующей форме: (3.2) В Формула(3. 1) и(3. 2) объединить и получить уравнение баланса массы в общем виде. ^ irso8AiL + ^ — GrGeGi = O.(3.3) Уравнение 3.
Значение, если оно записано в наиболее распространенных случаях, будет более ясным, когда весь поток, направленный в объем, проходит перпендикулярно области A19 a Наружный поток-как показано на рисунке, участок L2 3.2. В других точках на поверхности управления поток идет параллельно поверхности управления. В этих условиях e2b2l2-51crAl + ^ — =0.(3.4) величина U называется скорость потока или средней скорости и определяется соотношением (3.5) Один Предполагается, что плотность на поверхности интегрирования постоянна, а скорость направлена вдоль нормали. Определите уравнение массового расхода i7 Как это (3.6) (3. Семь) И если RI2 задано в функции m, то выражение 3.
7) смогите быстро быть интегрировано. Часто один или оба потока являются постоянными. Если оба потока постоянны и равны, то процесс будет Стационарный Эти уравнения легко обобщить, так что вы можете выразить баланс 4-й компонент многокомпонентной системы. Если показано на рисунке 3. 2, мы имеем: (3. Девять) Здесь падение 1-го компонента по химической реакции в контрольном объеме (кг! Это уже второе).Здесь » поток диффузии через управляющую поверхность равен、 Это важно. Соответствующим термином является Формула(3. 9) легкий для того чтобы input. Формула(3. 9) смогите быть написано в компонент. При суммировании эти уравнения дают уравнение (3. 7) в случае Р-компонентной системы н 2-й= о.
Хотя некоторые из представленных здесь уравнений могут показаться очень очевидными, метод вывода оказывается полезным для получения уравнений баланса энергии и импульса. Результат не так прост. Пример 3.1 В декартовых координатах D. элемент площади A представлен как1hau, но для круглой трубы удобнее использовать Полярный Coordinates. So, NA-rHrHO (0-угол полюса). (3. 5) подставляя соотношение(1), Вы получаете: 2yah4 И (NgH * 0-(2)’ О, да. Переменная 0 не входит в уравнение (1) из-за своей осевой симметрии. (2) вычислите Интеграл, и вы получите простой результат.
Один б-немного. (3) Как это Н / _ ttahOyag1 _ seekingOlP2 2/8 (4) Плотность 98% Так… Серная кислота при 00°С равна 1,8567 а / сл3 Черный. 0.9•1000•1.86•3.14•502•10 «9 Восемь = 1,64 кг / с (или 5900 кг / ч). Число Рейнольдса также calculated. In в этом случае расчет должен производиться на средней скорости. Ks_ _ 1000> 1.86-0.45 „50 IO-3 _ N 47.0-10“ 3 _89°* Вязкость(47,0 cps) была взята из страницы 373 Перри и умножена на 10, чтобы преобразовать ее в нужную единицу измерения (кг / м * с).
- Что касается однородности размеров, вы всегда должны проверять .Примеры, рассматриваемые в расчете, должны включать метры, килограммы и секунды. Число Рейнольдса меньше 2100, поэтому предположение о ламинарном течении оправдано. Пример 3.2 В хорошо перемешанную емкость подается вода со скоростью 60 кг / ч, а хлорид натрия (NaCl) в количестве 12 кг / ч. полученный раствор вытекает из емкости со скоростью 48 кг / ч. Для Хорошее смешивание, концентрация отработанной жидкости соответствует концентрации в баке, а скорость получения материала и удаления раствора не превышает.
Начало работы в танке Есть 40 кг чистой воды、 Рассчитайте концентрацию исходящего раствора (массовую долю соли) через 1 час. Уравнение (3. 7) и(3. 9) должны быть решены вместе. Сначала рассмотрим соль Аллана (компонент а). (1) PL (»*Newton fluid is considered. In в случае неньютоновской среды стенка стенки может отличаться от нуля. пусть chl-массовая доля соли в растворе, выходящем из резервуара.
Затем (LxA) ^ н-я ’ А1 + −4?^ — =0 (2) (1xA Дм 48gA-12 + M-A + xa ^ 0=.(3) Эту формулу можно упростить, используя формулу баланса общей массы «’*- И’1 + — ^ = 0(4) Или 48-(60 + 12)+ ^-=0。(5) Потому что есть 2 входных потока (вода и соль)= 60 + 12.Отсюда в качестве скорости накопления получается значение 24 КГ / ч. Уравнение (5)уметь интегрировать、 ЛГ = 24Т + л / А>(6) Для рассматриваемой задачи МО = 40 кг. Если вы назначаете эти выражения в выражении (3), то остаются только 2 переменные xA и m. Это правда? Один 48 * a −12+(24t 4-40)+ 24 * A =0.(7 )) Когда вы отделяете переменную, она выглядит так: / yt 24Т + 40 Да.
Интеграция и последующее преобразование (9 )) для m = 1 час массовая доля xA = 0,126.Формула (9), согласно здравому смыслу, показывает, что xA стремится к 1/6, когда время t очень велико. Задачи 3. 1.Если все величины выражены в молях, то уравнение(3. 7) и(3. 9) напишите аналогичное уравнение.= моль / ч и т. д. 3. 2. Смесь 40 кмоль / ч непрерывно подается в дистилляционную установку, молярная доля толуола составляет 0,35, а молярная доля бензола-0,65.Продукт перегонки заканчивается в 2 потока. Содержит 5% бензола, поступающего на завод. Во 2-м потоке молярная доля бензола составляет 0,99. найти расход как потока кмоль / ч, так и состава концентрированного потока Toruen.
Накопления в системе не происходит. 3. 3.Обычный дистилляционный аппарат заполнен жидкой смесью бензола и толуола с молярной концентрацией 60% и 40% соответственно, 60 кмоль. Состав пара, выходящего из установки、 Связанные с составом оставшейся жидкости по уравнению Ха Вау.〜 ’——-。 1 +(а-1) ХД Где уА и Ха-молярные доли бензола в парах и жидкостях соответственно, а а-относительная летучесть и постоянная, равная 4, О7.Каков состав восстановленного дистиллята? Если дистилляция продолжается до тех пор, пока в установке остается 30 молей жидкости ЭКСКУРСИЯ?
Растягивающийся поток в круглой трубе с гладкой стенкой, число Рейнольдса 110 000 профиль скорости выглядит так: один И-Итах Найдите значение этого случая. Интеграция упрощается, когда Выполните подстановку y = n-g. _l 3. о.. Распределение скорости в пленке жидкости, которая течет слоями вдоль вертикальной стенки, может быть выражено следующим уравнением: 1 * Нажмите Кнопку Vert И Сожгите. „«„*SK ° R°STB на расстоянии°t “ да. м ст „О и верхнее месторождение“ 2 ° й 01 ° темп прироста в СТИ ’ дисконт СТИ равн Б. проходят через толщу слоя воды, стекающей вниз DL ширина вертикальной стенки, Exp.°D H°DY 380 л / мин, а его температура 16°C.
P ppstGh ’/ B5°Ln long 78’7» — * a труба, средняя скорость потока пара 3 м / с, абсолютное давление 14 атм, температура 320°C. yn PML llefarydd AR ran llywodraeth Cymru. Абсолютная «^ 10 a ta 7eX pa * ur b-s ’ 4 при p5vna в это время средняя скорость? ХХГзХьТтаблХ’и «также вычисляет определение параметра пара’ 11ттках ’0 «eSCIM coli ° » 94%H28O4.In добавление к порошку фосфита, вода добавлена в достаточных количествах для того чтобы произвести фосфат 40% во время процесса stapion. Возрождение rXoo Loe форной кислоты и гипса (Ca8O4. 2Н, о) * rhMTT°гррррррр и gsmitsitecha, общая масса остается постоянной.
Смотрите также:
| Утилизация вторичных (побочных) энергоресурсов (ВЭР) | Уравнение баланса энергии |
| Балансовые уравнения. Вводные замечания о гидродинамике | Баланс количества движения |
