Оглавление:





Аддитивный расчет теплопроводности жидкостей.
Аддитивный расчет теплопроводности жидкостей. Из уравнений(х-5)и (Х-6) (теория Бриджмена) видно, что теплопроводность K должна зависеть от скорости распространения звука и молярного объема жидкости. Обе эти величины являются аддитивными, и если структура молекулы известна, то ее можно вычислить путем суммирования фракций. О молярной скорости звукаСм. формулу (II-12) доля облигаций приведена в таблице. Р-13, Для расчета молярного объема жидкости, могут быть использованы многие методы, описанные в гл. II. Если обе переменные в рассматриваемом уравнении являются аддитивными, то следует предположить, что добавление добавочных фракций также может быть использовано для расчета коэффициента теплопроводности X. Действительно, и/ или, согласно бриджмену) диаметр молекулы A = D (X-18).
Сакиадис и Котес [30]разработали следующий метод расчета теплопроводности: основываясь на теории Бриджмена, они предположили, что энергия, передаваемая в 1 моль, равна удельной теплоте вещества, а расстояние между молекулами а меньше расстояния между центрами молекул D (следы). Людмила Фирмаль
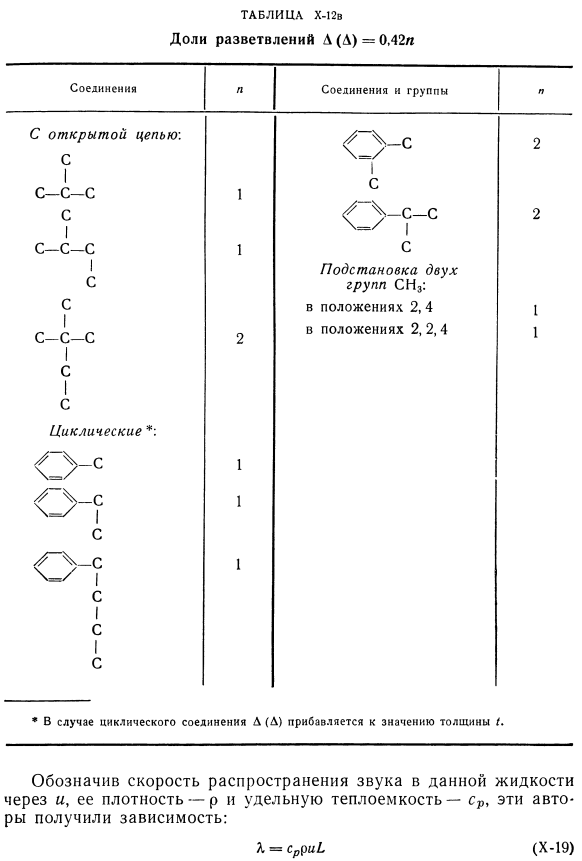
- Для циклических соединений L (L)добавляется к толщине I. По данным кф, эти авторы получили зависимость-удельная теплоемкость с ее плотностью-Р, которая указывает на скорость распространения звука в жидкостях: (Х-19) Х = РСП Причем значение получается из Формулы (11-12)-1) и вычисляется молярная скорость звука: (Х-20) Где m-молекулярная масса вещества. С/и-молярная скорость звука, которая вычисляется аддитивно по доле группы (таблица 11-14). 2-е значение (расстояние между соседними молекулами I), необходимое для вычисления X по формуле (X-19), равно、 *При замене группы циклических соединений, доля группы добавляется к толщине И. ** Если подставить C1 или Br, то его позиция безразлична. От его имени Инз будет парапозицией. Найти с помощью метода сложения вычисления D-значений, предложенного Сакиадисом и Котесом. В таблице приведены фракции для расчета величины D при температуре 19°С. х-12. Значение D представлено A (10-8 см).D (D) любой группы указывает на исправление и добавляется к D. = 4>-( РПР РПР ^ пр В7 ПЛ * Армированный пластик.
- Сакиадис и Котес оценили экстраполяцию молекул до температуры 0°К ( / , = 0) в контакте друг с другом и до критической температуры, при которой плотность жидкости и пара равна, согласно правилам Кайе и Маттиаса. Где I * расстояние A между соседними молекулами. D-расстояние между центрами соседних молекул, A; Ppr = P / Pkr » уменьшение плотности. pkr-это плотность в критической точке. RPL-это плотность при температуре плавления. Армированный пластик. pl-Rpl / Pcr-снижение плотности при температуре плавления. ГПЛ-МП; TaYag pr = G. l / Gkr-падение температуры в точке плавления. ТКР-критическая температура.
Вместо параметров точки плавления, можно заменить параметры точки кипения. Однако, первый способ лучше подходит. Людмила Фирмаль
- Плотность жидкости rpl можно рассчитать по формулам Сакиадиса и Котеса (на основе правил Кайете и Маттиаса). 1-0. Сорок восемь Pn., = Р р <Х-22) 1-0. Сорок восемь 1 кр. Вы можете вычислить скорость звука и уравнение (X-20) и, основываясь на суммировании определения молярной скорости звука (см. таблицу P-14), определить требуемое значение с помощью сложения вычислений D и I на основе уравнения (X-21).Значение X в выражении X-19. Рид и Шервуд [1], описанный метод расчета, теоретически обоснован, но на практике дает реальную погрешность (в среднем 5-15%, до 57%).Поэтому нет никакого преимущества перед простой эмпирической формулой.

