Оглавление:

Изгиб балок поперечной нагрузкой за пределом упругости
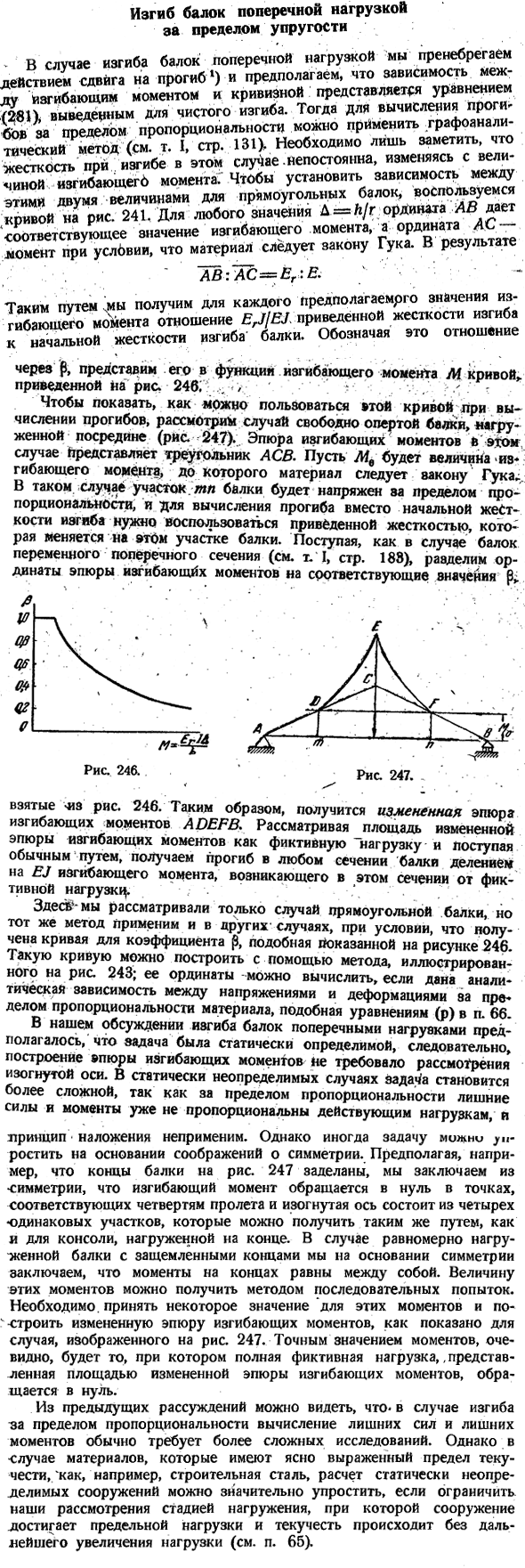
Изгиб балки из-за боковой нагрузки, превышающей предел упругости Игнорировать изгиб балки из-за боковых нагрузок Он представлен функцией изгибающего момента кривой M, показанной на рисунке 1, через§. 246;;..-•<> ./ ’. ’Я не уверен. ** ’: Чтобы показать, как эта кривая может быть использована при расчете прогиба, рассмотрим случай свободно опирающихся балок. Нагрузка прикладывается к центру (рис. 247).Фигура изгибающего момента в этом случае представляет собой треугольник ACB. Размер изгибающего момента материала M9 подчиняется закону крюка.:
- В этом случае поперечное сечение балки искажается сверх пропорционального предела, поэтому для расчета прогиба вместо первоначальной изгибной жесткости необходимо использовать уменьшение жесткости, которая изменяется с этим поперечным сечением балки. I, как и в случае балок переменного сечения (см. T. I, P. 188), мы делим момент изгибающих продольных фигур на каждое значение Fc. Рисунок 247. Ага. Ф Ф Ф В Да. Рисунок 246.
Взято из рисунка 246.Таким образом, мы получаем модифицированную диаграмму изгибающего момента Айерва. «Изгибающий момент как мнимый момент» принимая во внимание площадь измененной фигуры нагрузки и действуя обычным образом, изгибающий момент, возникающий в этом сечении от мнимой нагрузки, делится на EJ для получения прогиба в любом сечении балки. Здесь мы рассматривали только случай прямоугольной балки, но если получим кривую с коэффициентом p, аналогичную показанной на рисунке 246, то такой же метод можно применить и в других случаях cases. As с помощью формулы (Р), приведенной в пункте 66, можно рассчитать ее ординату, если между напряжением и деформацией задана аналитическая зависимость, превышающая предел пропорциональности материала.
При описании изгиба балок боковыми нагрузками задача предполагалась статически детерминированной, поэтому в графике изгибающего момента не было необходимости рассматривать криволинейную ось. Людмила Фирмаль
Если он не может быть определен статически, превышение пропорционального предела усложняет набор, поскольку избыточные силы и моменты больше не пропорциональны рабочей нагрузке.
Принцип наложения не применяется. Однако упрощение самых маленьких задач может основываться на соображениях симметрии. Например, если конец балки на фиг. 247 замыкается, изгибающий момент исчезает в точке, соответствующей 4-й минуте-1 пролета, заключая, что кривая оси состоит из 4 одинаковых участков и может быть получена таким же образом, как и последняя нагруженная консоль. Для равномерно нагруженных балок с защемленными концами мы приходим к выводу, что, основываясь на симметрии, моменты концов равны друг другу.
- Величину этих моментов можно получить методом непрерывного trials. As как показано на рисунке 247, необходимо принять определенные значения для этих моментов и создать диаграмму коррекции для изгибающих моментов. Точное значение момента-это мнимая суммарная нагрузка, которая представлена областью изменения диаграммы изгибающего момента.
Из предыдущих рассуждений видно, что при изгибе за пределы пропорционального предела расчет избыточных сил и избыточных моментов обычно требует более сложных исследований. Людмила Фирмаль
Однако для материалов с четко определенным пределом текучести, таких как конструкционная сталь, расчет статически неопределенных структур может быть значительно упрощен, если структура достигает конечной нагрузки и принимается во внимание на стадии нагрузки, где ликвидность генерируется без дальнейшего увеличения нагрузки (см. п.65).
Смотрите также:
Предмет сопротивление материалов: сопромат

