Оглавление:

Продольный изгиб стержней переменного поперечного сечения
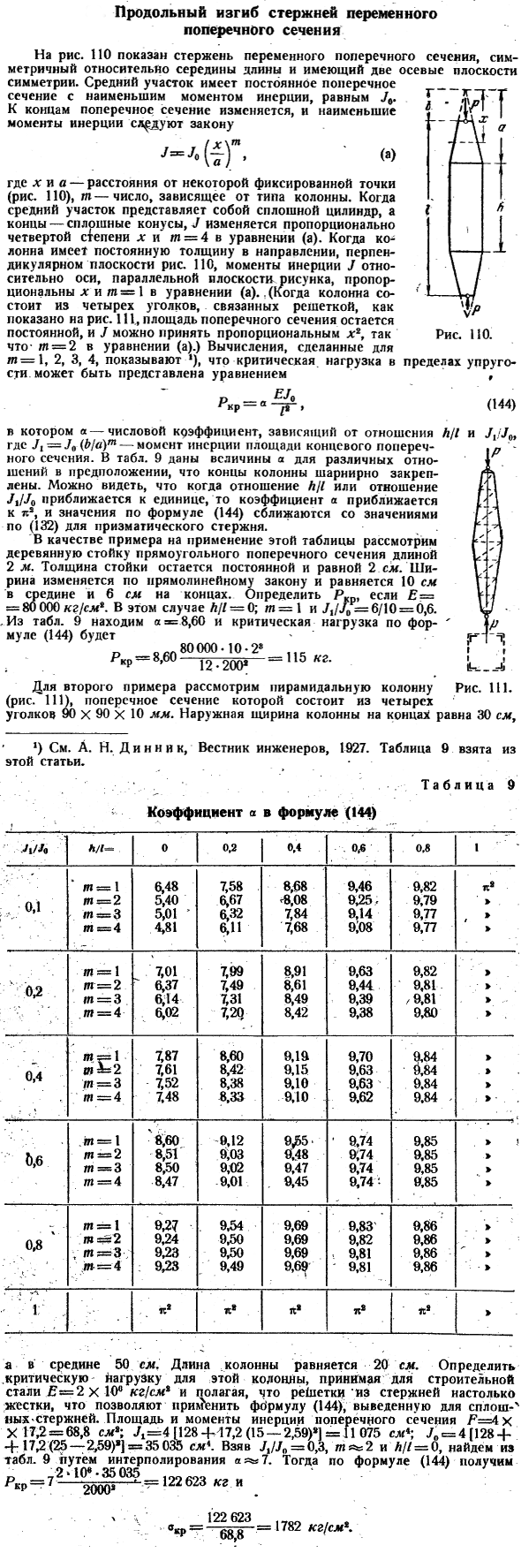
Продольный изгиб стержней переменного сечения ПА фигугури симметричен относительно центра длины, показывая переменное поперечное сечение стержня, имеющего две осесимметричные плоскости. Средняя секция имеет постоянное поперечное сечение с наименьшим моментом инерции, равным Uv.
- Наконец, поперечное сечение изменяется, и минимальный момент инерции следует закону Ух… (ля) Где x и a-расстояния от неподвижной точки (рис. 110), а m-число, соответствующее типу столбца. Если центральная часть представляет собой сплошной цилиндр, а оба конца-сплошной конус, то пропорционально мощности формулы (а), 4 x и m = 4, 3 изменяется.
Если толщина столба постоянна в направлении, перпендикулярном плоскости фигуры, то момент инерции y к оси, параллельной плоскости фигуры, пропорционален формуле (а) x и m = 1. Людмила Фирмаль
(Как показано на рисунке 111, если колонна состоит из 4 углов, Соединенных решеткой, то площадь поперечного сечения остается постоянной, а Y пропорциональна x, поэтому в Формуле (a)/ l = 2.
Расчет, созданный для m-1, 2, 3, 4) критическая нагрузка в Эластике рассчитывается по формуле П * п = а £уя (144) Где a-числовой коэффициент, зависящий от отношения hfl к Y,/ Y0、 Где V / = V0 (b / a) m-момент инерции участка конца section. In стол. На рисунке 9 показаны значения для a в различных отношениях в предположении, что оба конца столбца закреплены шарнирно.
Вы можете видеть, что когда отношение A // или отношение Y, / Y0 приближается к 1, коэффициент a приближается к za, а значение формулы (144) приближается к значению стержня призмы (132). В качестве примера применения этого стола рассмотрим деревянную подставку с прямоугольным сечением длиной 2 м.
- Толщина подставки остается постоянной и равна 2 см. Ширина колеблется по простому закону: середина-10 см, край-6 см. Для E—80 000 кг / см*, определите R-p. In в этом случае A / / = 0; m = 1 и V, / V0 = 6 / 10 = 0,6 из таблицы. 9 а = 8,60, а критическая нагрузка по формуле (144) равна Rkr = 8.60 115 кг. 12-200 * Ф Во втором примере рассмотрим пирамидальную колонну(рис. 111).
Свое поперечное сечение состоит из 90×90×10 mm с 4 углами. Людмила Фирмаль
Наружная ширина ряда кромок составляет 30 см. Рисунок 111. «) А. Н. Д. см. Ниник, Вестник инженеров, 1927. Таблица 9 Коэффициент формулы (144) a • ». JX используется! ч; л/# -. 0 0.2 0.4. *. 0 * 6. 0.8 1 Т-1 6.48 7.58. 8.68 9.46 9.82 в V * м = 2 5.40.6.67 <8.08 9.25 г. 9.79. *. Т-3 5.01> 6.32 7.84 9.14 9.77> Т-4.4.81 6.11 7.689 イ089. 77> Т = 1%. 7.01 7.99 8.91 9.63 9.82 > ;: О, 2. м = 2> 6.37 7.49. 8.61 9.44. * * 9.81. •「 。 Т = 3, 6.14 7.31 8.49 9.39, 9.81 * М = 4. 6.02 / 7.20 8.42 9.38 9.80> 。 。 。 — Пи! * Т * 2. 7.87 ’8.60 9.19 9.70 9.84 0.4:7.61 8.42 9.15 9.63•Вт б Т.== 3•7.52 8.38 9.10 9.63 ’。 9.84 в% М = 4•7.48 8.33 9.10 я не уверен. 9.62 ′ 9.84,•%’ 。 * М = 1 ′ 8.60. — О. I29£5 ’* 9.74 9.85 1. 。 ■ ’ ! > ö, 6 t = 2 8.51 9.03 9.48 9.74 9.85 т. −3 8.50 9.02 9.47 9.74 9.85> т.— 4•8.47 −9.01 я не уверен. 。 9.45 9.74 я 9.85> Т.-1 ’8.27•9.54 9.69 9.83′ 9.86> 0.8 в’. ТФ 2 9.24 9.50 9.69 9.82 9.86•」 Т Т = 3; 9.23 9.50 9.69 я 9.81. 9.86 。 * * Я■ГХ (***Т = 4:9.23 9.49 9.69-9.81 9.86 Вт *. .1 ^ 1•> 1′.*. ** Л * Л * * Р * > Длина колонны −20 см.
Учитывая, что сталь I = 2×10°кг / см, решетка стержня очень жесткая и Формула (144) получена для твердого стержня. Площадь поперечного сечения и момент инерции/?= 4х х 17,2 = 68.8 см; JX используется= 4 [1284-17.2(15-2.59)*] = 11075 см *; У0 = 4(1284-Ф-17.2(25-72.59)*] = 35 035 см *.Когда JJJ0 = 0.3, получаем 2, hfl-0、 Табуляция. 9 путем интерполяции 7.Тогда из Формулы (144) получим _2″10 *•35 035. P * p = 7-2000 * ’ ^ ’ ^ KZ и C * P =-688 = 1782 кг1см * ’
Смотрите также:
Предмет сопротивление материалов: сопромат

