



- Если условие (14.1) не выполняется, то температура в охлажденном (или нагретом) теле зависит не только от времени, но и другими словами, разные части тела Разные темпы. Зависимость 1 = — fix, y, 2, r) в этом случае может быть получена интегрированием нестационарного дифференциального уравнения теплопроводности. Уравнение、 Учитывается любой объем и энергетический баланс в организме. Выбранный объем ограничен замкнутой поверхностью F.
Если в объеме корпуса нет источника тепла и раковины, то общее Тепловой поток через поверхность F согласно (8.2)、 Q = = 4 ″ zqdF(14.8) Равна скорости изменения энтальпии (количества тепла) вещества, заключенного в объеме (14.9) По теореме Остроградского-Гаусса ^ в сфере туризма » = Ф див qdV. (14.10) в q = — K град /и затем divx Xgrad. / = П2 / ДФ dx2 + dz2 ’ И затем При сравнении формул (14.9) и (14.10)、 kV2tdV = \ СР ^ — дв. (14.11) Равенство (14.11) справедливо для произвольно выбранных томов, поэтому подынтегральные функции также равны друг другу. И затем… в ^ 72(= д (/ДМ (14.12) Где » X /(cp) — коэффициент теплопроводности.
Это нестационарное дифференциальное уравнение теплопроводности. Для его закрепления необходимо задать начальные условия определения температуры ионов, которые необходимо учитывать Объектом в первый момент времени является r = 0, граничное условие, определяющее законы температуры или теплообмена на границах объекта. В теплопередаче принята классификация граничных условий. Я добрый-устанавливаю температуру поверхности геля. II вид-устанавливается плотность теплового потока на поверхности тела. III тип-поверхность тела представляет собой теплообменник со средой известной температуры в соответствии с законом Ньютона (9.1). IV тип-рассматриваемое тело находится в тесном контакте с другим телом.
При решении стационарных задач теплопроводности использовались граничные условия типа 1 для типа 8.3 и типа 3 для типа 12.2. Анализ решений различных нестационарных задач Условия описаны в специальной литературе. Здесь мы рассмотрим только 1 из них-постоянную температуру/ х и охлаждение бесконечной пластины в среде при постоянном коэффициенте Теплопередача(рис. 14.1).
Если рассматриваемое поперечное сечение находится далеко от края, то распределение температуры по сечению пластины конечных размеров почти такое же, как и у бесконечной На расстоянии более чем в 10 раз превышающем толщину пластины) Для этого 1-го случая (температура изменяется только вдоль толщины пластины) уравнение (14.12) принимает вид: dx2 ad2t / = ДТ / ДТ(14.13) В исходном состоянии Zt_0 = / 0 =минусы (.(14.14) Граничное условие типа 3 получено из баланса 2 тепловых потоков. От глубины к поверхности охлаждающего тела Подходит за счет теплопроводности-X (d / / dx) r » ft и удаления Передача тепла теплоносителю?
Из-за условия симметрии температурного поля при x = 0 (^t_o = O. (14.16) Аналитическое решение задачи (14.13) — (14.16) 1 обычно дается в безразмерном виде. Рисунок 14.1 к заявлению о проблеме охлаждения Новое блюдо 2 раковины^ + зп » КГУ» потому что(Р «Х») Х н-я Хехр (- ПФО). (14.17) Где k = (/- /a)/ (/o-U)является безразмерным Температура, p * — корень характеристического уравнения ctgp = pn / Bi. 1 методы решения такого рода задач рассматриваются в специальных науках, предметной физике, и не предусмотрены в данном кратком курсе. Вы можете проверить точность решения.
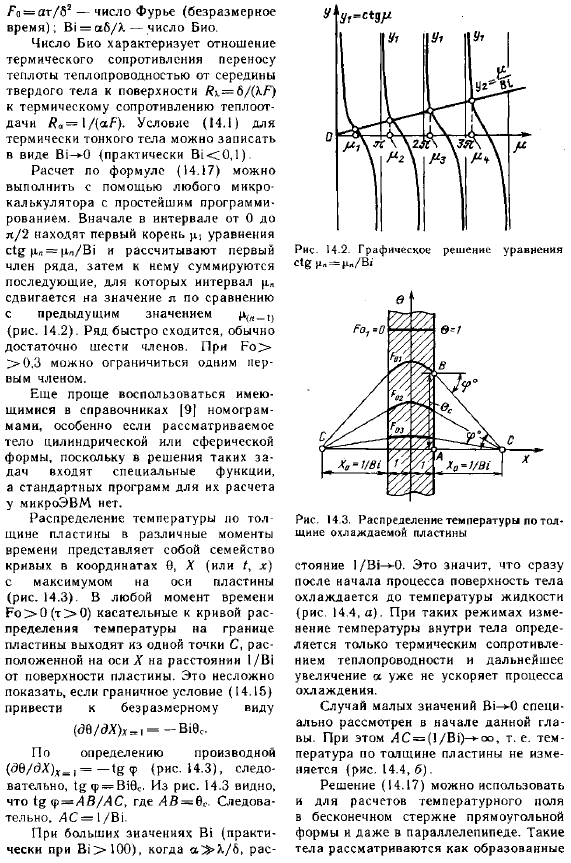
Подставляя начальное уравнение, а также начальные и граничные условия для n. / ’O = ar / b2 — число Фурье (безразмерное время). Bi = a6 / X-это число био. Число смещений характеризует соотношение теплопередачи и теплопередачи за счет теплопроводности твердых тел от центра к поверхности относительно теплового сопротивления теплопередачи Я /(АФ).Термически тонкое состояние объекта(14.1) может быть описано в виде Bi-*-0 (фактически Bi 0.1). Расчеты по формуле (14.17) можно выполнить с помощью любого микрокалькулятора с самым простым программированием.
Во-первых, в диапазоне от 0 до s / 2 мы находим первый корень pi уравнения ctg P, rt = p» / Bi и вычислить первый член ряда и добавить к нему следующий член. Поэтому интервал сдвигается на величину l по сравнению с предыдущим значением (рис.14.2).Линия Он сходится быстро, обычно 6 членов достаточно. Для Fo > > 0.3, вы можете ограничить до первого 1 члена. Решение таких задач включает в себя следующее, Поэтому еще проще использовать номограммы, имеющиеся в справочнике[9], особенно если форма рассматриваемого объекта цилиндрическая или сферическая.
- Распределение температуры по толщине пластины в различных точках представляет собой группу кривых в координатах 0, X (или t, x)с максимальным значением на оси пластины (рис.14.3). В любой момент времени E0> 0 (m> 0) тангенс кривой распределения температуры границы пластины появляется на расстоянии 1 / Bi от поверхности в 1 точке C на оси X. Пластина. Это может легко указать, сводится ли граничное условие (14.15) к безразмерной форме (30 / dX) x»i- -Bi9f. По определению производной (д0 / дх) Ке / = — тг Ф(рис. 14.3), следовательно, тг Ф = орудий Б-10.14.3 тг (Р = ^ АВ / АС, где АВ ^ КК. Следовательно, AC = I / Bi. Если значение Bi велико(фактически Bi> 100), то С другой стороны, 14.2.
Графические решения этг Уравнения Рисунок 14 3.Распределение температуры в направлении толщины охлаждающей плиты Стоя л / би — *-0.Это означает, что сразу после начала процесса поверхность корпуса остынет до температуры жидкости(рис. 14.4, а). Определяется только термическим сопротивлением теплопроводности, и дальнейшее увеличение а уже не ускорит процесс охлаждения. Если значение Bi-I) невелико, то его специально рассматривали в начале этого chapter. In в этом случае LS =(!/ B|) — » — oo, то есть температура не изменяется с толщиной пластины(рис. 14.4, b).
Вы также можете использовать решение (14.17) для расчета температурного поля бесконечного прямоугольного стержня и параллелепипеда. Такое объединение считается образованным. 9. ФО-0 е-я Джи?、 Икс 9. Рис. 14.4.
Распределение температуры Bi — *в направлении толщины охлаждающей пластины при oo (a) и Bi — * О (b) Пересечение 2 или 3 взаимно перпендикулярных бесконечных пластин и безразмерной температуры в любой точке будет иметь вид произведения безразмерной температуры Это тело образовано пересекающимися бесконечными пластинами. Например, электрическая печь с температурой 14,1 900 ° C, диаметром 50 мм и длиной 2 м, вычисляет время нагрева круглой стальной полосы 20 ° C от 0 до 800°.
В пределах определенного интервала температуры топления частей, теплофизические свойства металла и условия теплообмена меняют значительно, для того чтобы выполнить точный расчет、 Разделите этот интервал на меньшие интервалы и найдите общее время нагрева как sum.
To проиллюстрируйте этот метод, выполните только приблизительную оценку сразу для всей температуры Интервал (метод расчета не зависит от размера интервала температур нагрева).Теплофизические свойства металла и условия теплообмена учитываются в среднем и заданном интервалах Температура нагрева/и −400°C В [ссылка 115], найти теплофизические свойства стали с/ «= 400С: Л» = −42.7 Вт /(мК); p «-7682 кг / М5: s- = * 682 Дж /(КГК); в = 0,8. / f −900°C и= 40(1°C: Хж- −7.63-10 * 2 Вт /(м-К); в»-155.1-10- м?/ С; РГХ-0,717; РГС-0,678; 0. = 1 / ГФ^ 1 /(273 + + 900)= 8.5-10″ 4 1 /К.
Коэффициент теплопередачи естественной конвекции по аналогии с примером (10.2) Ну * = 0,5 (Кржррж) 0 25 (РЖ / Ргэ) 0= = 0.5(2.17 −10 *•0.717)°-、с.(0.717 / 0.678)°•«= 5.66。 Хе КРФ = ^^ ^ 1₽ * Вт = 9.81 ~ 3.5 ~ IQ-4(900-400)-0.053(155.1-10〜6)2 = 2.17-IO4; А «= ну » л » / д = = 5.66■7.63•10″ 2 / 0.05 = 8.6 ж /(м2 * к). Тепловой поток за счет излучения от стенок печи с температурой/ f. найти стержень по аналогии с примером (11.1). Ци 2-iCtfxdt [(ТЖ / 100) ’ — (ГС / 100> «|- = 0.8-5.67-3.14 0.05-2 — (ш)‘] −24,°’ БТ- Коэффициент теплопередачи излучением a, = Q (2 / lt / / (/k -/) = = 24-103 / 3.14 −0.05 −2(900-400)= = 153 Вт / (м2 * к).
Общий коэффициент теплопередачи выглядит следующим образом а = а> + ал = 8,6 + 153 = 162 Вт /(мг > К). При высоких температурах теплопередача за счет излучения является доминирующей, обратите внимание на величину а без существенного errors. It не удалось проигнорировать и счет. Для выбора метода расчета времени нагрева можно использовать «Bi-ar / l»-162-0.025 / 42.7 вычислить—0.095. Следует отметить, что численное значение Bi содержит теплопроводность нагреваемого объекта (металла), а численное значение NuM содержит теплопроводность газа.
Так Как Bi 0.1.Нагретый объект можно рассматривать как термически тонкий, и можно использовать формулу(14.7).Из этой формулы мы вычисляем£ / V ’= 4 / rf (площадь обоих концов Игнорировать), получаем Ов * ’ж»’ г 4 * ’ ш» о 682-7682-0.05, 000-800. 4-162 С.
Смотрите также:
| Виды теплового расчета теплообменников | Понятие о численных методах решения задач теплопроводности |
| Расчет нагрева и охлаждения термически тонких тел | Состав и основные характеристики твердого топлива |
