Оглавление:

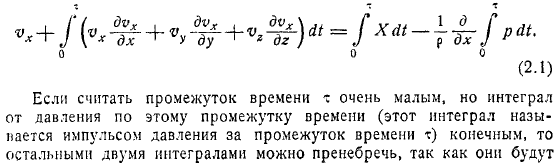

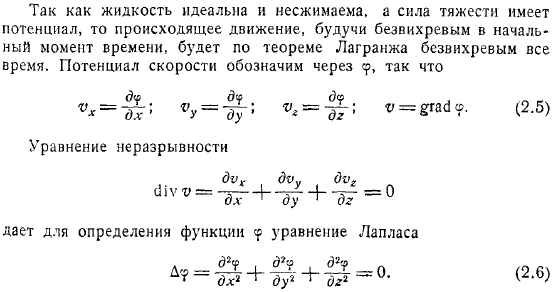



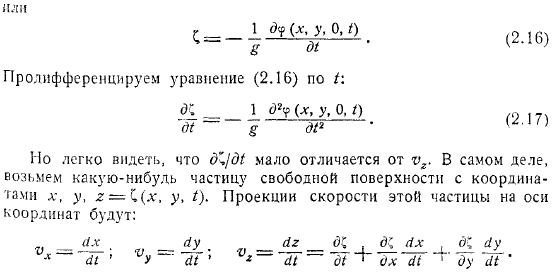

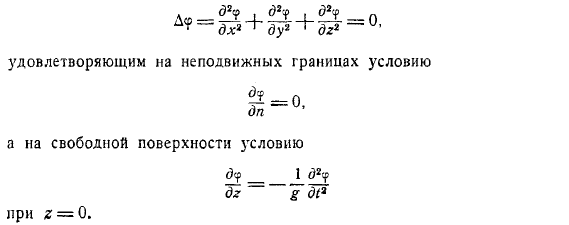

Основные уравнения
Рассмотрим волны гидромеханики, возникающие под действием силы тяжести под воздействием идеальной жидкости равномерной несжимаемости. Некоторые неподвижные поверхности (например, дно озера) имеют нижние и боковые границы, а сверху они становятся свободными поверхностями, на которых видны волны. Волны возникают в первый момент, когда происходит возмущение жидкости, то есть отклонение состояния жидкости от равновесного.
Равновесное состояние жидкости, скорость всех частиц равна нулю, а свободная поверхность жидкости равна. Начальное возмущение жидкости состоит из частей: возмущение свободной поверхности жидкости и наличие типов волн ненулевых скоростей различной жидкости. Предполагается, что начальное возмущение жидкости обусловлено тем, что она действует только на свободную поверхность жидкости.
- Например, медленно замачивая часть твердого тела, деформируя свободную поверхность жидкости, а затем сразу же удаляя тело, вы получите возмущение свободной поверхности жидкости, и начальная скорость всех частиц, конечно же, будет равна нулю.
- Предположим, что помимо нормального нормального давления на поверхность жидкости действует дополнительное давление, как и везде, для получения начальной скорости частиц жидкости с горизонтальной свободной поверхностью. Такое дополнительное давление может возникать на поверхности воды, например, в случае внезапных порывов ветра.
Предполагается, что эти дополнительные давления действовали в течение очень короткого времени. Людмила Фирмаль
Интегрируйте уравнение движения Эйлера в главе за этот период и получите его из первого уравнения Эйлера, учитывая то, что было в начале разрыва. Если мы считаем, что временной интервал очень мал, но интеграл давления за этот период (называемый импульсом давления за этот период) конечен, то другими интегралами можно пренебречь.
Кроме того, укажите, где вы подробно изучили действие мгновенной силы на жидкость через условия мгновенный импульс, как в главе. Тогда получается, что проекция скорости, вызванная импульсами давления, действующими на свободную поверхность жидкости, определяется по формуле. Именно поэтому движение, возникающее при действии ударного давления на свободную поверхность жидкости, имеет потенциал скорости, и поэтому вихря в ней нет.
- Формула функции зависит от всех координат, но из результатов, описанных выше, можно предположить, что она задается только на поверхности жидкости.
- Как найти функцию в любой точке жидкости обсуждается в. Как упоминалось в главах, мы имеем не-вращательное движение независимо.
Может рассматриваться как возникающее под действием мгновенного давления с импульсами. Поскольку жидкость идеальна и несжимаема, а гравитация имеет потенциал, то движение, которое происходит, не является вращательным в первый момент, поэтому оно всегда не является вращательным по теореме Лагранжа. Потенциал скорости.
Уравнение неразрывности. Дайте уравнение Лапласа для определения функции. Людмила Фирмаль
Как видно из главы, основные уравнения гидродинамики невращательного движения упрощаются и принимают вид. Указывает на возможность воздействия внешней силы.
Если ось направлена вертикально вверх, то потенциал силы тяжести, действующей на единицу массы определяется по формуле. Поскольку движение очень медленное, мы предполагаем, что термин может быть проигнорирован в выражении. Итак, мы пишем следующее.
Вы не можете написать дополнительные функции, потому что вместо этого вы можете сделать следующее. Чтобы было проще, введем функцию, которая отбросит начало будущей функции, и запишем ее следующим образом. Выражение является решением уравнения, которое используется для решения задачи.
Но существует множество решений уравнения Лапласа, и для того, чтобы выбрать из них единственное, которое необходимо, необходимо обратиться к граничным и начальным условиям. Граница жидкости состоит из неподвижной поверхности (дна) и свободной поверхности. Вблизи неподвижной поверхности жидкость течет параллельно такой поверхности, поэтому на неподвижной поверхности нормальная составляющая скорости жидкости равна нулю.
Поместите начало координат в точке на этой поверхности со свободной поверхностью в положении равновесия в виде плоскости. Давление на свободную поверхность жидкости. Постоянная величина, равная давлению газа над жидкостью (атмосферному давлению), обусловлена непрерывным изменением давления при переходе от жидкости к газу.
Поэтому на свободной поверхности. Чтобы сделать его проще, включите его, введя эту функцию вместо функции. Отбросьте значок функции снова и, наконец, напишите уравнение в виде. Приведите уравнение свободной поверхности времени-момента в форму. Затем из уравнения и условия на свободной поверхности.
Поскольку колебания жидкости предполагается очень малыми, уравнение может (а не) получить значение и, следовательно, его можно записать в виде. Дифференцируя уравнения. Однако нетрудно заметить, что их почти нет. Фактически, мы берем частицу свободной поверхности с координатами.
Проекция на оси координат скоростей этой частицы выглядит так. Последняя формула показывает производную по времени сложной функции, которая изменяется во времени (так как частицы, принадлежащие свободной поверхности, движутся не только в вертикальном направлении, но и в горизонтальном). Но последние члена можно проигнорировать, если предположить, что они очень малы, то есть касательная плоскость к свободной поверхности почти не отличается от горизонтальной.
Поэтому он почти равен на свободной поверхности. И опять же, как было сказано выше, это равенство можно считать (вместо этого) выполненным. Напомним, что вместо этого вы можете, наконец, написать.
Теперь мы соберем все полученные результаты. Невращательное волновое движение идеальной несжимаемой жидкости, возникающее под действием силы тяжести, определяется по формуле. Где функция является решением уравнения Лапласа. Удовлетворяют условию с фиксированной границей. И условия на свободной поверхности.

