Оглавление:


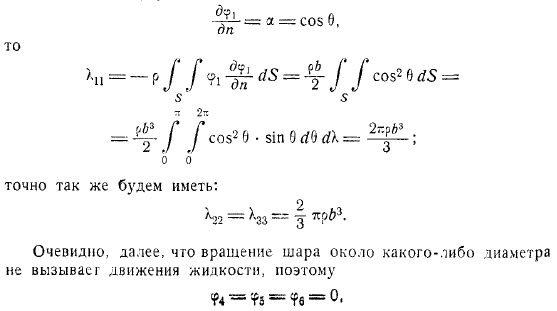



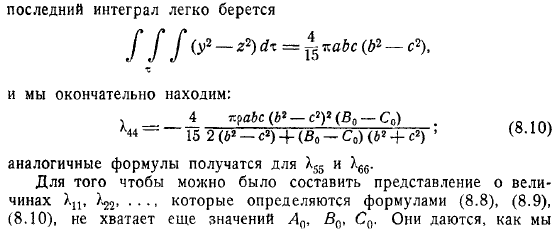



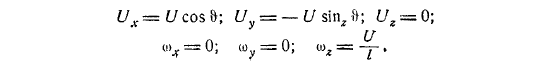


Примеры
Далее мы рассмотрим конкретных примера. Прежде всего, следует отметить гидромеханику, что в своем конкретном случае формула значительно упрощается. Если поверхность имеет оси симметрии, перпендикулярные друг другу (например, если у вас есть эллипсоидальная поверхность).
Направляя ось движущейся системы координат вдоль оси симметрии поверхности, можно легко увидеть, что в этом случае все коэффициенты с разными индексами будут равны нулю, а формула кинетической энергии примет простой вид. А выражение силы пишется в простой форме. В качестве реакций при движении тела первого примера рассмотрим движение шара по радиусу.
- Если шар движется в направлении оси с единичной скоростью, то это выглядит так. Здесь сферические координаты центрируются в начале шара, а ось полюса ориентирована вдоль оси.
- С вершины сферы. Точно так же. Кроме того, понятно, что вращение шара вокруг диаметра не вызывает движения жидкости.
Следовательно. Итак, длина шара. В этом случае удобнее использовать фиксированную систему координат. Людмила Фирмаль
Это связано с тем, что в данном случае формула человеческой силы подходит для любой системы координат. Очевидно. Таким образом, по формуле, сила потока на шаре уменьшается до силы, приложенной к центру шара.
Если на массу шара влияет сила, приложенная к центру шара, то движение шара в жидкости определяется следующим уравнением. Видно, что поступательное движение шара в жидкости происходит потому, что оно происходит в пустоте, если масса шара увеличивается на дополнительную массу. Последняя равна половине массы жидкости, вытесненной шаром.
- Теперь рассмотрим движение полуосевого трехосного эллипсоида. Функция. Возьмите поверхность эллипса значение. Кроме того, выполняется граничное условие.
- Поэтому мы находим его быстро, но по теореме Гаусса Вот объем. Точно так же это выглядит следующим образом.
Больше. Таким образом, на поверхности эллипсоида. По формуле Гаусса Окончательный интеграл легко берется. И, наконец, найти. Получена аналогичная формула. Для того, чтобы иметь возможность выяснить количество, которое определяется по формуле. И все же здесь не хватает ценности.
Это можно увидеть. Легко увидеть, что это зависит только от. Дело в том, что если ввести вместо значения равенство, то оно выглядит так. Людмила Фирмаль
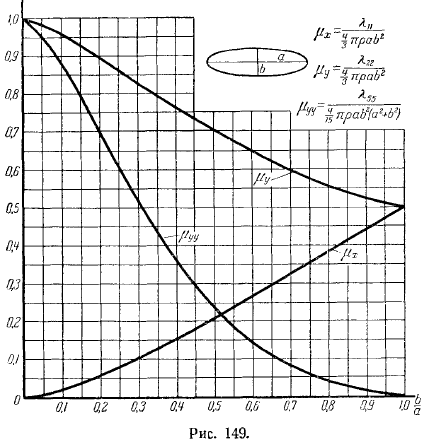
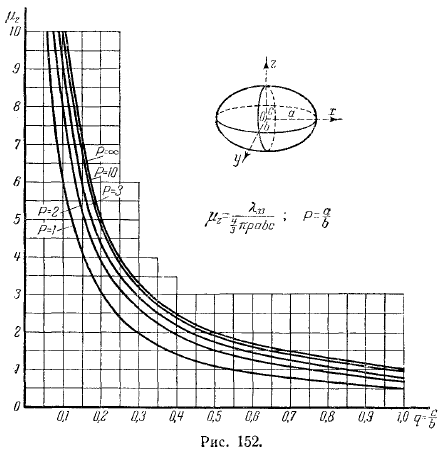
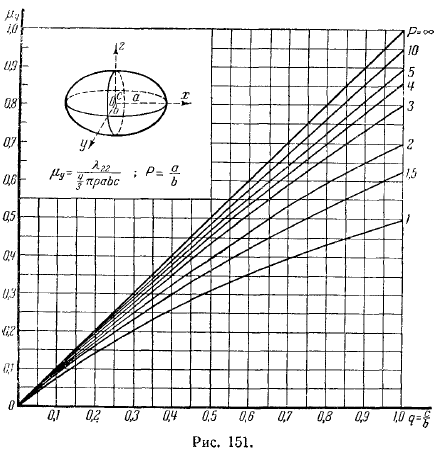
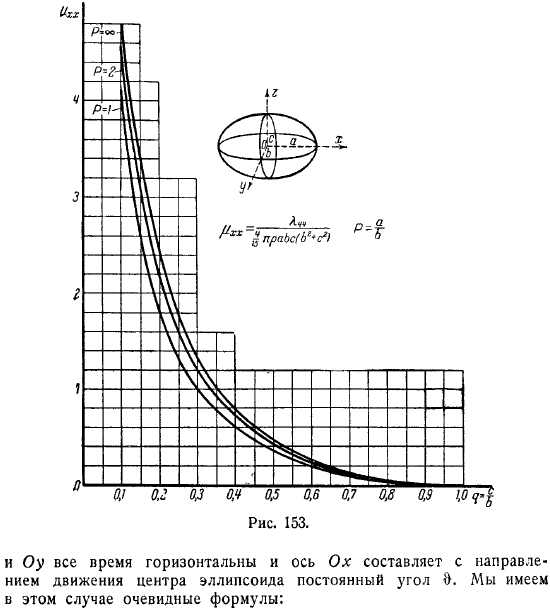
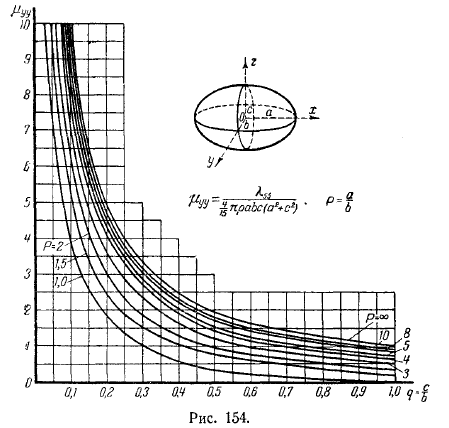
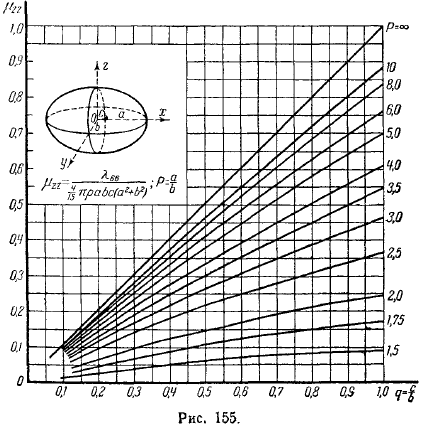
Гуревич и Риман рассчитали эти значения тела по инерции в функции и дали график. Исходя из этого, легко вычисляется коэффициент присоединенной массы любого эллипсоида.
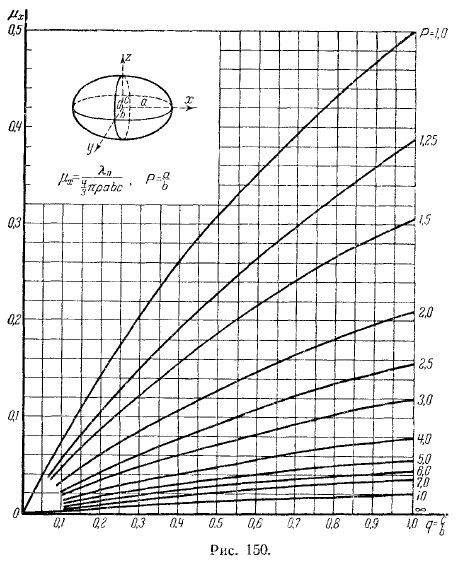
Приведены примеры этих графиков. Соответствует сфероиду. Применять здесь значение в функции. Случай с мячом берется в следующих случаях: по результатам, полученным выше. Вы можете сделать следующее. Фигура соответствует трехосному эллипсоиду.
Это показано на рисунке. Форма семейства кривых в зависимости от параметров по абсциссе строится всюду количество. Она расписана в каждом из них. Центром эллипсоида является скорость радиуса горизонтальной окружности, а осью эллипсоида является.
Образуют касательную и нормальную проекции силы. Таким образом, вертикальная составляющая дает дополнительную центробежную силу, а кажущееся увеличение массы эллипсоида составляет. Кроме того, пара действует на организм мгновенно.
Эта пара исчезает только в том случае, если центр эллипсоида смещен в направлении любой из осей. Наличие этой пары тесно связано с наличием тангенциальной. Дело в том, что ясно, что энергия жидкости при рассматриваемом равномерном движении эллипсоида всегда остается одинаковой.
Сила явно не производит работы. Наоборот, пока она не равна нулю, пара будет работать, но и силы должны работать, чтобы суммарная работа сил и пар была равна нулю. Итак, формула выглядит так.

