Оглавление:


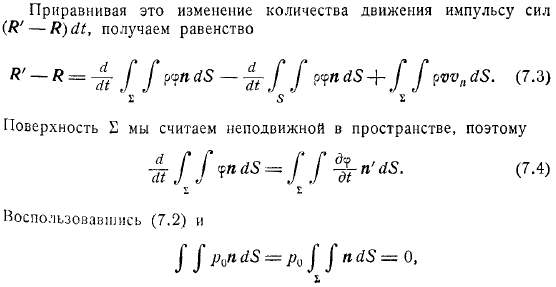

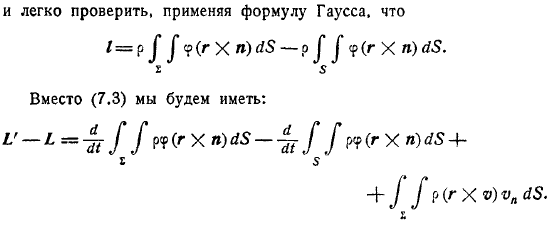



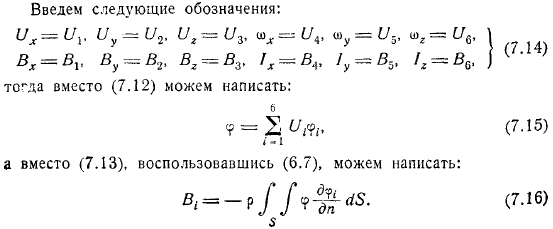





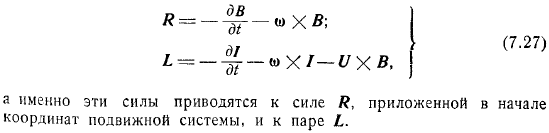

Расчет гидродинамических реакций при движении тела
Движение твердых тел в неограниченной жидкости. Рассмотрим движение жидкости, вызванное движением объекта, окруженного поверхностью, с бесконечной, несжимаемой идеальной жидкостью, которая бесконечно. В этом случае гидромеханика предполагается, что нет никакой внешней силы, действующей на жидкость, и нет никакого вихря в движении жидкости. Для представления рассматриваемого мгновенного потенциала скорости по проекция скорости равна.
Уравнение неразрывности указывает, что функция должна удовлетворять уравнению Лапласа по всей области течения, то есть вне поверхности. Подумайте о возможности как уникальный. В каждой точке на поверхности должны быть выполнены твердого тела в безграничной жидкости и граничные условия.
- Где скорость имеет проекцию на точку той же поверхности, что и нормаль к поверхности. Для ясности предположим, что Нормаль находится вне поверхности, то есть внутри жидкости.
- Условие, что жидкость бесконечно стационарна, приводит к граничному условию. Можно предположить, что мы стремимся к нулю при одинаковой величине.
Фактически, сферическая координата вводится вокруг начала координат, и она постепенно расширяется в окрестности ряда бесконечных точек. Людмила Фирмаль
Отбрасывание некритических констант имеет следующую форму разложения. Сферическая функция. Предположим, у вас есть сфера с радиусом, центрированным в начале координат. Из-за несжимаемости жидкости скорость потока через нее должна быть равна нулю.
И с тех пор. Для того чтобы определить функцию, необходимо знать величину, то есть составляющую скорости точек этой поверхности перпендикулярно поверхности. Но известно, что распределение скорости твердого тела полностью определяется установкой скорости точки этого объекта и установкой угловой скорости вращения объекта.
Выбираем начало координат этой точки, которое обозначается вектором скорости этой точки (которая считается неподвижной связью с телом), и через вектор угловой скорости вращения тела, для скорости тела и любой точки, получаем формулу. Людмила Фирмаль
Итак, вблизи точки бесконечности происходит разложение формы. Вот радиус-вектор точки относительно точки.
В проекции на координатные оси это выглядит так. Для простоты Косинус угла складывается из нормалей поверхности с осями. Точка поверхности. Поэтому условие принимает следующий вид. Эта функция указывает, что она должна отображаться в следующем формате.
Кроме того, все функции должны удовлетворять уравнениям и условиям. На поверхности эти функции должны соответствовать условиям С тех пор условия были четко соблюдены Примеры. Поскольку условия больше не зависят от векторов, все функций определяются выбором формы поверхности и системы координат.
Если сравнить условие с общим условием, то можно увидеть, что функция соответствует случаю движения тела в следующих случаях. То есть, когда тело движется параллельно оси с единичной скоростью. Функции имеют аналогичное значение. Аналогично функция соответствует следующему случаю. То есть, если тело вращается вокруг оси с угловой скоростью вращения, равной.
Например, определите эти функции, когда тело является трехосным эллипсоидом. Найдено решение задачи о потоках, обтекающих эллипсоид, бесконечная скорость которого параллельна положительной оси. Если вы возьмете формулу, вы получите решение. Накладывая на поток, представленный этим решением, поток.
Получить потенциал скорости в ответ на равномерное движение параллельно оси со скоростью, равной единице Скорость в бесконечно неподвижной жидкости соответствует движению эллипсоида, параллельного оси. Точно так же, это выглядит так. Обратите внимание, что на поверхности есть очевидное равенство.
Эта функция может быть получена из следующих соображений: эта функция удовлетворяет уравнению Лапласа для легкого. Бесконечность, эта функция стремится к нулю как степень. Но на поверхности есть равенство. Для этого Так что вы также можете написать.
Мы выбираем этот путь откуда? Он появится на поверхности. Если сравнить это условие с условиями функции, то можно сделать вывод. Считается, что это не вращательное движение. Величины, распределенные вдоль поверхности, образуют систему таких импульсов.
Они представлены основными векторами импульсов и их основными моментами относительно начала координат. Вектор называется ударной силой, а вектор-ударной парой. Уравнения теперь находятся в очень простой форме. Уравнение движения твердого тела легко описывается системой координат, которая связана с телом так, что оно не.
То же самое. Соедините оси с твердыми телами без перемещения и не перемещайте оси в пространстве. И предположим, что в какой-то момент обе системы осей совпадают. Помнить это. Преимущество движущейся системы координат заключается в том, что функция зависит от времени, так как граничные условия в этом случае явно не зависят от времени.
В этой формуле только компонент вектора, определяющего движение твердого тела, зависит от времени, и эти компоненты получаются на оси движущейся координаты. Создайте вектор. У нас есть. Вводится следующая нотация. Вместо этого, вы можете написать.
Вместо этого, вы можете использовать и написать следующее. Я введу обозначения. Тогда мы получаем из следующей базовой формулы. Это легко показать. На самом деле, его можно приложить к областям окруженным поверхностью и зеленой формулой левая сторона равна нулю, потому что.
Если у вас есть сфера с центром в начале большого радиуса, подынтегральная функция первого интеграла справа равна. Интеграл — это порядок, который исчезает как. Следовательно. Это эквивалентно. Поэтому коэффициент независимости будет только.
Эти коэффициенты называются вложениями. Для того чтобы точнее определить их значения, мы также рассчитываем кинетическую энергию жидкости. Здесь интеграция осуществляется по всей. В этом случае сначала рассмотрим интеграл замкнутой площади между поверхностями, согласно формулам, приведенным в главе.
Как уже упоминалось выше, нетрудно заметить, что последний Интеграл стремится к нулю по мере бесконечного увеличения радиуса сферы. Таким образом, мы получаем конечное значение для жизненной силы всей бесконечной жидкости вне поверхности. Теперь мы находим следующее, используя выражение и определение коэффициентов.
Выражения теперь могут быть выражены очень простым способом. Теперь вернемся к задаче расчета силы, действующей со стороны жидкости на твердое тело. Эти силы нашли формулу главного вектора и главного момента. Используя нотацию, вы можете написать.
Однако следует иметь в виду, что в этих формулах производная по времени используется в предположении, что вектор вычисляется в фиксированной системе координат. Если вы хотите использовать производную по времени от суммы, вычисленной в движущейся системе координат, используйте знак частной производной. Вектор представляет собой основной вектор системы мгновенных импульсов давления.
Отложить от начала фиксированной координаты. Представляет собой скорость конца вектора, очевидно, относительную скорость конца этого вектора. Начало координат рассматривается относительно системы координат, где началом координат является точка оси, параллельная оси движущейся системы.
Но абсолютная скорость точки равна геометрической сумме относительной и переносимой скоростей, последняя в данном случае является. Это связано с тем, что переносное движение требует понимания поворота системы координат под углом. Получаем основную формулу в расчетах, ситуация несколько сложнее.
Вектор — это система мгновенных импульсов давления относительно начала координат, то есть главного момента фиксированной системы координат. Но при расчете мы сравниваем значения последовательных моментов основного момента системы мгновенных импульсов давления относительно разных точек, то есть начала координат движущейся системы в этих последовательных точках.
Поэтому он отличается от дополнительный член, то есть скорость изменения моментов, взятых вблизи движущегося. Вы знаете, что главный момент системы сил для одной точки равен главному моменту той же системы сил для другой, равен моменту главного вектора системы сил, приложенного в точке ко. Для одного и того же исходного положения момента радиус-вектор положения начала координат системы перемещения момента равен, поэтому происходит дополнительное изменение момента, скорость изменения будет.
Вы получаете основное выражение. Таким образом, влияние со стороны потока на организм определяется по следующей формуле. То есть эти силы сводятся к силе, приложенной к паре с началом координат движущейся системы.

