Оглавление:





Кристаллы со сложной структурой элементарной ячейки
- Приведенный выше вывод основан на том, что если рассматривать объект как континуум и применять теорию упругости, то собственные колебания низкочастотной длинноволновой кристаллической решетки получаются достаточно точно. Я обнаружил, что это относится к 1-D цепи.
Однако этот вывод справедлив Для моноатомного твердого тела только 1 атом содержится в его ячейке массива (примером такого кристалла является решетка меди).1-D цепь, состоящая из одинаковых частиц, также служит моделью одного атомного тела, каждое из которых имеет 1 частицу. Как видно по Борну*, для кристалла с единичной решеткой, содержащей несколько различных частиц(например, CaCl, Cacaco и др.), колебание дискретной кристаллической решетки существенно отличается от колебания континуума в некоторой точке. Для уточнения задачи возьмем одномерную модель, то есть цепочку упруго связанных частиц, в которой масса m (M> m) изменяется попеременно.
Если анизотропия кристалла не учитывается, то частота обоих поперечных колебаний совпадает. Людмила Фирмаль
Обозначают продольное смещение частицы мяты. Уравнение движения аналогично (40.3) и имеет вид М£н + х (25.- м.)- М1..1)= 0、 (42.1) щч. + х(2р.- Е.- / ) «0. Я ищу решение, которое работает с сплошным цветом волна: R |.„Vevd -*“, (42.2) — Иp-ka ’=2naa/ X (a-расстояние между 2 последовательными идентичными частицами), где X-длина волны. Черный. (42.3) Подставляя в уравнение движения (42.2) в уравнение движения(42.1)、 (2х-М О *)А-х(1 + е)) б-0, — х(1 + е-*)л +(2х-ТТГ ’)Б-0; (42.4) За исключением A и B、 ТМ о ‘ — 2х (т + м)АР + 2х’ ’(1-соѕ ф)= 0 2= ^¡11+ t±/Л / ‘+г+ 2tL/₈₈].
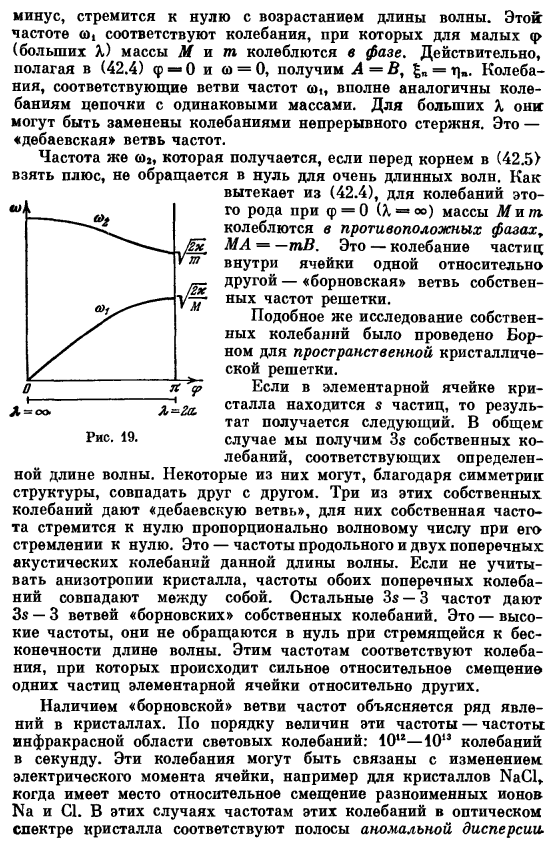
Каждому значению волнового числа соответствует 2 частоты, а не 1 (Рис.19) w иo, [(42.5) 1 находится в корне из 2 знаков. Частота. Это получается, если вы получаете знак перед корнем в(42.5). • ) Например, родился М., Гепперт-Мейерм. Теория Твердого Тела! Дополнительные сведения см. В разделе практическое руководство. М.: ОНТИ, 1938, с. 211 ff. Минусы стремятся к нулю с увеличением длины волны. Эта частота0 соответствует колебанию, при котором масса Mit колеблется в фазе с малымp (большим). фактически, если задать (42.4) φ= 0 иa = 0, то получим A = B,= m. колебания, соответствующие частотной ветвиn, полностью аналогичны колебаниям цепей той же массы.
Если а большое, то его можно заменить непрерывной вибрацией штанги. Это устройство ветви частоты. Частоты, полученные с плюсом перед корнями (42.5), не исчезают при очень длинных волнах. Как видно из (42.4), при таком виде колебаний приp = 0 (X —o») масса Мит колеблется в противофазе(MA-Tv).Это вибрация относительно других частиц в одной ячейке. Это костная ветвь собственной частоты решетки. Аналогичное исследование собственных колебаний было проведено Борном о пространственной кристаллической решетке. Если в единичной решетке кристалла имеются частицы, то результатом будет: в общем случае определены Без длины волны.
Некоторые из них, благодаря симметрии конструкции, могут совпадать друг с другом.3 из этих собственных колебаний дают «устройство бифуркации»; в тех случаях собственная частота стремится к нулю пропорционально волновому числу, если оно стремится к нулю. Это частоты продольных и 2 поперечных акустических колебаний определенной длины волны. Остальные частоты Za-3 дают 3 ветви рожденных Za собственных колебаний. Это высокие частоты, которые не исчезают на бесконечных длинах волн.
- Эти частоты соответствуют колебаниям, при которых некоторые частицы в элементарной ячейке смещаются относительно других частиц. Наличие «костной» ветви частоты объясняет многие явления crystals. In по порядку величины эти частоты являются частотами инфракрасной области световых колебаний: 1 вибрация 10-10 дюймов в секунду.
Эти колебания могут быть связаны с изменением электрического момента ячейки, например, в случае кристаллов iac1, когда происходит относительное смещение различных ионов N8 и C1 occurs. In в этих случаях частота этих колебаний в оптическом спектре Кристалла соответствует полосе аномальной дисперсии. И поглощение. Эти собственные частоты в инфракрасном диапазоне называются частотами остаточных лучей.
Это явление комбинационного рассеяния, или эффект комбинационного рассеяния кристаллов. Людмила Фирмаль
Вообще говоря, рожденная вибрация и вибрация устройства теплового движения вызывают изменение оптических свойств кристалла, вызывая рассеяние света molecule. In в этом случае изменение частоты происходит, когда устройство рассеивается тепловой волной точно так же, как описано выше. Спектр рассеянного света показывает частоту v±W. v-это частота падающего света, а w-частота волны колебания Бора, при которой свет рассеивается в этом направлении.
Длина этой упругой волны X по-прежнему задается в соотношении (41.15).Поскольку частота Борнеевских колебаний очень слабо зависит от длины волны, то частота падающего света изменяется одинаково для рассеянного света в разных directions. In кроме того, по сравнению с частотой вибрации устройства той же длины волны, изменение частоты падающего света является большим, потому что W борновской вибрации очень большой, его можно легко наблюдать с помощью обычных спектральных приборов. Необходимо внести некоторые изменения в теорию теплоемкости.
То есть если кристалл состоит из единичной ячейки(по 3 частицы в каждой), то существует 3sW степеней свободы и, соответственно, 3sw собственной вибрации, то есть 3W принадлежит ветви Дебая, а остальное-кости branch. In при представлении энергии все эти собственные колебания следует учитывать, что приводит к незначительному изменению формул (41.5) и (41.14).Однако эти изменения играют роль только в средней температуре range. At при низких температурах закон кубического устройства (41.9)остается в силе, а при высоких температурах-классическое представление удельной теплоемкости (27).
Следует отметить, что в представленной здесь теории теплоемкости твердых тел атомы решетки (или ионы) везде считаются точками. Таким образом, энергия возбуждения атомов до соответствующей удельной теплоты не учитывалась. В некоторых случаях, когда для атома возможен переход с очень малым изменением энергии, удельная теплоемкость, соответствующая этим переходам, может играть очень большую роль. Это происходит, например, против кристаллов сульфата гадолиния при температуре около 2 К, когда теплоемкость увеличивается в несколько сотен раз. Кроме того, в представленной теории предполагалось, что атомы ке обмениваются, а кристаллическая структура не изменяется с температурой.
Часто, как пример твердого раствора (латуни), вокруг определенной температуры происходит резкое увеличение теплоемкости порядка 1 ккал/ К.
Смотрите также:
| Колебания одномерной цепочки упругосвязанных частиц | Равновесное излучение. Формула Планка |
| Теория теплоемкости твердых тел (продолжение) | Трудности, приведшие к статистикам Бозе |

