Оглавление:




Колебания одномерной цепочки упругосвязанных частиц
- Рассмотрим набор частиц, образующих цепочку в одном измерении. Частицы в равновесном состоянии расположены вместе на одинаковом расстоянии а (постоянная цепи). в этом случае сила, действующая на частицы, возникает только от 2 соседних частиц и зависит от относительного смещения направления цепи. Их смещение (квазиупругая сила) пропорционально разнице. Тогда сила, действующая на ПТГ (n-1) палка со второй стороны равна —- х(5.- пошли.-、)、 5 ″ — это смещение N-й частицы из положения равновесия.
Постоянный. вся сила, действующая на n-ю частицу, очевидно, n-1 + ^ n, n + 1, и уравнение движения имеет вид: (40.1) (40.2) «»± ((- En-14-2 & ₁ — 6п ₊ ₁) −0. (40.3) Сначала рассмотрим бесконечную (двунаправленную) chain. To сделав это, я получаю набор уравнений(40.3), где n выполняется на всех целочисленных значениях от-°до+».Найти нормальные колебания этой системы в виде монохроматических бегущих волн (40.4) ВеличинаР, определяющий разность фаз колебаний соседних частиц, пропорциональна волновому числу K = 2П / К. другими словами、 Φ= ka = 2la / L (40,5> следует отметить, что φ изменяется в интервале длины 2n.
Таким образом, покрываются все возможные колебания цепных частиц при распространении волны. Людмила Фирмаль
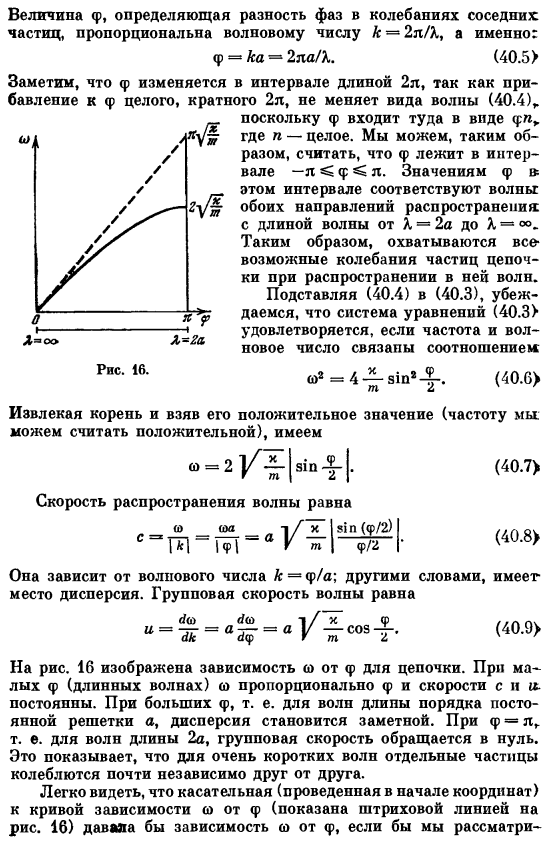
Потому что даже если мы добавим целое число, кратное 2n к Phi, форма волны(40.4) не изменится. Это можно сделать Сразу же предположим, что φ находится в интервале-l φC l. величина φ в этом интервале соответствует волне в обоих направлениях распространения с длиной волны X = 2a до A. Подставляя (40.4) в (40.3), можно видеть, что система уравнений(40.3>) удовлетворяется, если частота и волновое число связаны относительно a «= 4-^ — s1n’ — 2 -. Извлечение корня является положительным значением (частота Вы можете думать об этом как о положительном) (40.6> Два (40.7> Скорость волны С ТАНКОМ Т * 1-Г?1.
Это зависит от волнового числа k = y / a; другими словами、 Расположение дисперсии. Групповая скорость волны (40.8) (40.9> На рисунке 16 показана цепочка зависимостей шоу. Для малых φ (длинноволновых)0, φ и пропорциональна этим velocities. Permanent. In в случае большого φ, или длины волны порядка постоянной решетки a, дисперсия становится заметной. для φ=л, то есть, для волны длиной 2а, групповая скорость исчезает.
- Это указывает на то, что в очень коротких волнах отдельные частицы колеблются почти независимо друг от друга. Касательная к φ-зависимой кривой (показана пунктирной линией на рис. 16) (нарисована в начале координат) показывает, что ω зависит от φ следующим образом: Вибрация цепи походила на вибрацию твердого стержня. Этому же случаю соответствует начальное значение^ k / m для кривой, показанной на рисунке. 17.In дело в том, что скорость упругой волны в непрерывном стержне равна 1E! Равен P, где E-модуль Юнга, а p-плотность. Модуль Юнга равен отношению, вызванному ее относительной деформацией 40.11} Принимая во внимание= t / a, получим скорость непрерывного стержня p = 0 цепь.
Таким образом, мы видим, что мы можем вычислить разделенную длину волны в случае длинных волн(по сравнению с цепью Анни а), используя уравнение, связанное с continuum. It оказывается, даже для самой короткой волны (p = x, X = 2a) погрешность в частоте при применении непрерывной модели не так велика: o равно yUx / m, а не 2Ux / w. то есть примерно в 1,5 раза. Нас интересуют объекты ограниченного объема. Сделайте цепь состоящей из N + 2 частиц, а крайнюю-нулевой и (DO + 1)-й-фиксированной. Такие модели будут соответствовать твердому телу, закрепленному жестким wall. So, граничные условия следующие: 5.-0, ГМ-0.
Таким образом, в атоме происходит нормальное колебание ограниченной цепи. Людмила Фирмаль
Если взять линейную комбинацию из 2 волн, протекающих в обратном направлении в действительном виде, то получим конкретное решение задачи дифференциального уравнения (40. 12) [40. 3] 1 при граничном условии (1). 5.- A cos(at-фп + 7)+вcos (at + ФП + 7>), (40.13) Где A, B, 7 — » произвольные константы. Граница для выполнения условия£ ₀ — 0 (Все t)、 4 = — B, f, −7, = 7 Как это. = А икос(в-ФЛ + Ф) — в COS(в +фп + 7)]- — 2А грех (от + 7) грех ФП.
Условие, за которым следует −0 грех Ж + 1)р = О ф Подобный этому №.(40.14) 5″ = пост-грех (0т + г) Си Каждое из этих решений представляет собой нормальную вибрацию, и все частицы вибрируют с одинаковой частотой Все полученные N решений дают N нормальных колебаний, которые возможны в цепи с N степенями свободы. Частотаo, эти нормальные колебания изменяются в интервалах 0 w * 2 2л Они представляют собой стоячие волны длиной X = 2la / p,= 2a (N + i)/ k соответственно, определяемые из тех же условий, что и колебания непрерывного стержня (или струны).GV + l), что полуволна целого числа должна соответствовать по длине цепи.
Как мы видели, в случае длинных волн скорость распространения вдоль цепи будет очень близка к скорости волны непрерывного стержня той же плотности и модуля Юнга. Поэтому в этом случае частота нормальных колебаний приблизительно совпадает. Поэтому для длинных волн можно, по сути, использовать модель а continuum. In в частности, его можно использовать для расчета теплоемкости при низких температурах, когда только длинные волны (низкие частоты) имеют ярко выраженную energy.
Смотрите также:
| Теплоемкость двухатомных газов | Теория теплоемкости твердых тел (продолжение) |
| Теория теплоемкости твердых тел | Кристаллы со сложной структурой элементарной ячейки |

