Оглавление:





Применение квантовой статистики к осциллятору. Формула Планка для его средней энергии
- Примените квантовую статистику к гармоническому осциллятору, то есть к системе, в которой вид оператора Гамильтона равен 4 . Во-первых, вычислить среднюю энергию квантовая механика показывает, энергия такой системы важна Е. = («+1/2) — М <1>, » −0,1,2,…(37.1)) Все состояния, соответствующие этим возможным энергиям, едины. Предположим, что генератор является частью системы температуры.
Предполагается, что взаимодействие генератора с другими частями системы невелико (§ 10).Тогда, поскольку вероятность энергии 1 или другого элемента задается канонической формулой (35.1), вероятность z-го состояния равна Средняя энергия E равна Для его вычисления, как обычно, удобнее всего найти сумму состояний в первую очередь Если применить здесь общее соотношение (37.1), то оно выглядит так: Согласно уравнению (37.1) 1, сумма состояний равна r = 2 exP (37.2) Ряды, входящие в эту формулу, являются геометрическими рядами со знаменателями e-Lm,°, сумма которых равна (1-e_) −1.Следовательно、 Когда мы дифференцируем относительно O и умножаем на 6 *、 (37.3) Это уравнение планка для средней энергии осциллятора.
Согласно квантовой теории, с увеличением частоты температурно-зависимая часть энергии и теплоемкости также уменьшается. Людмила Фирмаль
Основным отличием от классического значения средней энергии осциллятора является средняя энергия Поведение резонатора в квантовой теории зависит от его собственной частоты. Учитывая систему, в которой энергия может быть представлена как сумма энергий осцилляторов (например, излучение твердых тел), квантовая теория говорит нам, что закон равномерного распределения энергий для степеней свободы не выполняется: энергия отдельных нормальных колебаний зависит от ее частоты.
Также из этого видно, что в квантовой теории температура, вообще говоря, не является универсальной мерой средней кинетической энергии, как это имеет место с точки зрения классической статистики. Соотношение между средней кинетической энергией K и температурой изменяется от системы к системе. Например, для генератора K это зависит от частоты. * — 4 дня-4 — ( ■ ¥■+ Член формулы для E, Ya> / 2, дает так называемую «нулевую энергию» осциллятора и остается конечным при абсолютном нуле температуры.
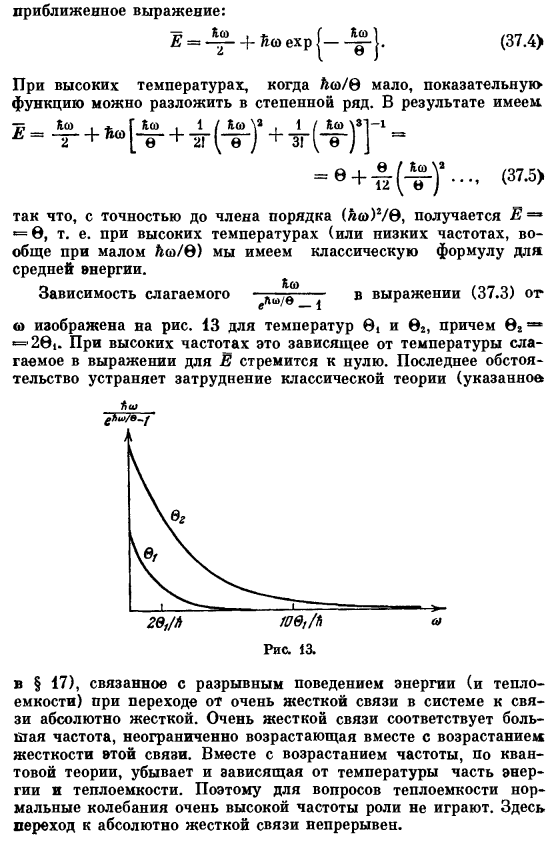
- Температурная зависимость средней энергии показана на рисунке. 12(т — Общ / б).Пунктирная линия дает зависимость в соответствии с классической теорией, согласно закону равномерного распределения энергии. При низких температурах или высоких частотах, где y0> f0 очень велик, при (37.3) знаменатель единицы пренебрежимо мал по сравнению с экспоненциальной функцией. Приближенное выражение: £ (37.4) При высоких температурах, если Л
На высоких частотах этот температурно-зависимый член уравнения е стремится к нулю.Последнее обстоятельство устраняет трудности классической теории В §17) он связан с прерывистой работой энергии(и теплоемкости) при переходе от очень жесткой связи в системе к абсолютно жесткой.Очень жесткое соединение соответствует большой частоте, которая неограниченно возрастает с увеличением жесткости этого соединения.Поэтому в вопросе теплоемкости обычные колебания очень высоких частот роли не играют.Здесь переход к совершенно плотному соединению происходит непрерывно. ( «) гггг Т»».
Если вы передадите его в исходные координаты линейным преобразованием, вы также получите Гауссовское распределение этих координат. Людмила Фирмаль
При применении、 u’e ^ + chu ^ — i’a (ДДх)] 1 H, (x} H, (x) замена 1 из факторов vyra. (6) (с) ¿У-(Г) Я<,») Где»=(1/2) » при применении этого равенства、 «‘<‘>=»Г (‘г’)1⁷ * ехр {- х » 1 Б(1- если вы замените r и замените x на y、 (171| * T » 21, 14?Г}-<3> Классическая формула Гауссовское распределение, распределение е =(р * + ж*»*) = » в、 Потому что в квантовой и классической механике средняя кинетическая энергия и средняя потенциальная энергия осцилляторов равны. Отсюда ? = 4(4 +)■<37.9> Уравнение Блоха (37.8) является гауссовским распределением с дисперсией (37.9).
Заметим, что если существует квази-другая система с произвольным числом степеней свободы, а не осциллятор с 1 степенью свободы, то ее координатное распределение также является гауссовым distribution. In фактически, мы вводим обычные координаты. Нормальные координаты статистически независимы друг от друга, и вероятность равна произведению формулы (37.8) относительно всех нормальных координат. То есть он представлен гауссовским распределением, но эти координаты, конечно, не являются статистически независимыми друг от друга.
Их средние квадраты и средние произведения могут быть получены аналогично описанному для осцилляторов, поэтому закон распределения по координатам полностью определен.
Смотрите также:
| Общие положения квантовой статистики равновесных состояний | Теплоемкость двухатомных газов |
| Термодинамические функции | Теория теплоемкости твердых тел |

