Оглавление:






Флуктуации плотности и числа частиц в системах с независимыми частицами (газы, растворы)
- Рассмотрим идеальный газ, занимающий объем V и содержащий N частиц (молекул).Выберите объем V в нем. Найти среднеквадратичное отклонение числа частиц n объема v от среднего значения n и вероятности Для идеального газа, где число частиц в этом объеме равно n, попадание различных молекул в объем v является независимым событием, согласно вышеприведенному выводу.
Отметим, что следующие выводы в равной степени применимы как к растворимым молекулам в растворе, так и к суспендированным коллоидным particles. In в случае газов (даже в поле внешних сил) эти выводы также применимы к флуктуациям числа частиц, скорость которых находится в определенном пределе, другими словами, флуктуациям числа частиц, расположенных в определенной области фазового пространства molecule.
Поэтому p к этому пределу стремится к нулю. p = fi / N рассматривается и представляет). Людмила Фирмаль
Дело в том, что, как следует, например, из регулярного выражения вероятности состояния газа, попадание различных молекул в эту область является независимым событием(вероятность состояния равна произведению вероятностей отдельных молекул).в этом случае n, конечно же, представляется в соответствии с распределением Максвелла. Вероятность того, что конкретная частица находится в объеме v, равна p = v / V. среднее число частиц в объеме v равно n = Np. Эффективность этой почти очевидной формулы можно увидеть следующим образом: если k-й числитель содержится, то 6″ = 1, если нет, то n 6,■= 0.Тогда, очевидно, Но…
Следовательно Б= 1•Р + 0-(1-р) — п; Таким же образом можно найти среднее квадратическое отклонение(u-n)* = n * — n. Во-первых, найдите pg. У нас есть 2-Я сумма распространяется на все пары частиц и \ > j. содержит JVW −1) / 2 членов. 6 — это » 1 или ноль, b?«= Б «и 6 * = б» = п и K и J 6Д-11п ’+ 2-1-0-(1-р) п + 0-0(1-п) — п’.Так… п — НП + Нин-ДП * (Н-Н) = А — Е * = ^(1-р)= п (1-п).
Если вероятность p-v / V очень мала и ничтожна по сравнению с единицей (другими словами, объем v очень мал v) при сравнении с, последнее выражение рисуется (с-С)* = Р (28.2) Эта формула играет огромную роль в теории всех явлений, связанных с флуктуациями. Плотность, усредненная по объему v, равна p-m (pM).Относительное отклонение числа частиц от среднего значения равно относительному отклонению плотности р от среднего значения. п-п _ РР Средний квадрат этого значения = 4- (28.3) НКН. «) Где L1-среднее число частиц на единицу объема (концентрация частиц).Поэтому относительное отклонение плотности уменьшается с увеличением объема и концентрации N.
- Вероятность того что общее число частиц объема V W содержит n частиц выражается следующей формулой: (28.1>. На самом деле вероятность того, что конкретная частица η находится в объеме v, а остальная-снаружи, равна по теореме умножения вероятности P „(1-p) “ — n. можно выбрать эти частицы e) / по теореме, вплоть до этого числа Чтобы получить вероятность, нужно умножить p» (1 — p) » _n и получить вероятность IV (n).Используя эту формулу вероятности, можно, конечно, найти уже полученную выше формулу для среднего числа b и среднего квадратичного отклонения (b-c)*.
Н =%з ©, (С-с) 1= 2 (С-Б) Ш ©. Такой же результат можно получить и при расчете этих сумм. Для большинства приложений важны 2 ограничительных случая. Мы это проанализируем. 1.In в случае Пуассона объем V намного больше, а N очень велик по сравнению с резанием. Этот случай имеет место, когда n — * ■постоянная (не обязательно большая) n = Np This. При переходе к пределу AG — ► < » Пуассон получает формулу. У ^(п)= е-«<(28.5) Эта формула может быть использована, например, для определения вероятности появления определенного количества коллоидных частиц в поле Ультра микроскоп. 2.
Вариации количества частиц в этих объемах Vₜ,… V случай с газом . Людмила Фирмаль
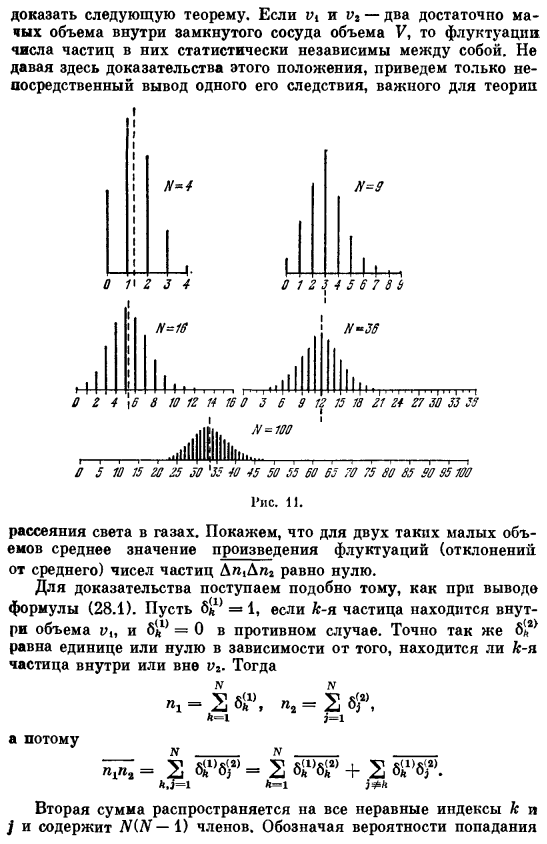
Если p = v / V произвольно, а N очень велико, то среднее число частиц в объеме, равном n = Np, будет очень большим из-за случая Лапласа. Если вы передадите предел N — * * » константа p в (28.4), вы получите выражение, соответствующее этому случаю. Его вывод показан во всех курсах теории вероятностей*). он имеет следующий вид: Поэтому, если N велико, можно использовать приближенное выражение. И ⁷ (n)=1exp I- «УЫрЦ -)) I (Н-Ноф?1. 2Lr(1-p) / ’ (28.6) В случае рисунка 11, p = 1/3, курс U ^(m)отображается для разных N. Если N= 100, то значение IV (n) уже очень хорошо соответствует формуле(28.6). ясно, что кривая (28.6) является»Гауссовой».
Симметрия opa: вероятность положительных и отрицательных отклонений одинакова Накоби. До сих пор мы рассматривали изменение числа частиц в конкретном объеме и выделяли его в объеме V. Вопрос, выражение вероятности распределения Число частиц Vₜ над большим объемом. Докажите следующую теорему: и если оба v и V являются 2 достаточно малыми объемами в замкнутом сосуде объема V, то колебания числа частиц в нем статистически независимы друг от друга other. No. Здесь мы приводим доказательства этого положения и даем только один прямой вывод из его результатов. Это важно для теории Рассеяние света в газах.
Такие 2 небольших объема указывают на то, что среднее значение произведения флуктуаций числа частиц (отклонений от среднего) равно нулю. Чтобы доказать это, мы действуем тем же способом, что и вывод формулы (28.1). если k-я частица находится внутри объема I> внутри 6 * ’= 1, если не 6/, то u = 0.Точности равен 1 частица внутри А потому что 2-Я сумма, а в том числе J и N (N — i) членов.
Обозначьте вероятность попадания для данной частицы в объеме y и ua соответственно через pt-vJV =и pa-vJV = hJN среднее (математическое ожидание) 6 * ’b’ * ’ получает следующее(Л#= /): ба » 6дж » = + 1-0-а(1-па)+ 0-1•(!- па) па + + 0-0-(1-па) (1-па)= ПТП,. Потому что всегда есть по крайней мере 2 PZ из 2 количеств b *1 ’или b), 2’is Ш’ — О. Так… «Л ^ ЛХ-пр. ДЛ₁Дпаа(пх-п.)(аа-па)=и, п-н н、- Если N очень велик по сравнению с Å, то hfiJN очень мал, а N — * ■<*> Ди. Дл=0.(28.7) В этом случае»коэффициент корреляции»вариации объема vₜ и 1>обращается также исчезает. хо…
Смотрите также:
| Влияние флуктуаций на предел чувствительности гальванометра | Молекулярное рассеяние света |
| Флуктуации объема, занятого газом или жидкостью. Предел чувствительности газового термометра | Принцип Больцмана |

