Оглавление:




Применение классической статистики к идеальному одноатомному газу
- Вышеуказанные положения в основном применимы к идеальному одноатомному газу. Предположим, что молекулы газа не взаимодействуют друг с другом, и состояние каждой молекулы N-газа характеризуется только ее расположением в пространстве и соответствующим импульсом. Поэтому степень свободы системы равна 3.V есть. Поверхность энергии этой системы, которую мы уже рассматривали(§ 1).
Как обычно, чтобы найти термодинамические величины газа, сначала нужно вычислить Интеграл состояния Z. Гамильтонова газовая функция имеет вид В этом случае потенциальная энергия U в сосуде будет равна zero. In степь, у будет большое положительное значение. Государственный интеграл-это y. dxNdyNdzN J expdp.. Интеграл V-0 по координатам внутренней точки. На стене U увеличивается, а e — » * стремится к нулю. Следовательно、 Которых J ехр {- к ^dxKdyₖdzₖ= Джей Джей Jdxdddyₖdzₖ-в、 Где V-объем контейнера.
В квантовой механике состояния различаются набором квантовых чисел и могут усредняться, например, по небольшим интервалам на шкале энергии. Людмила Фирмаль
Тип J exp (- p?ₓ/ 2m0)каждый Интеграл dpᵢₓ равна (2шв)’! в J ехр {-52} Д5 =(2л / ч0) ’ З = в «(2nwe), » /2. П по договоренности с начальством. 204 Интеграл состояния Z газа равен степени N-ti интеграла состояния 1 частицы r = V(2nm0) a / *: =В З = — НQ в V-в 0-в 2 лита. (12.2) (12.3> (12.4> Клан. Получить равновесие состояния с помощью (11.10) — 9Вт. У меня тоже. Используя (11.11) для энергии, получим следующую формулу: Ё — <[’in-ll’V Выражение (12.3) явно представляет собой уравнение Рона.
- Если есть моль газа, то я-константа Авогадро, равная N•= 6.02■102моль-1.Следовательно、 уе = Яг. С другой стороны, я = 8.31 Дж моль-к)、 112.5) K-R / N-1.38 ′ 10″» J / K получается. Это так называемая постоянная Больцмана. Таким образом, мы определили неопределенный коэффициент в соотношении b = kT. Где 6-температура в энергоблоке. Из (12.4) быстро получаем теплоемкость газа. 3nk 3″ (12.6> Наша общая теорема позволяет решить задачу о распределении скоростей, помимо установления термодинамических соотношений этих общих gases. In дело в том, что каждую молекулу газа можно считать»рассматриваемой системой», а остальные принадлежат термостату.
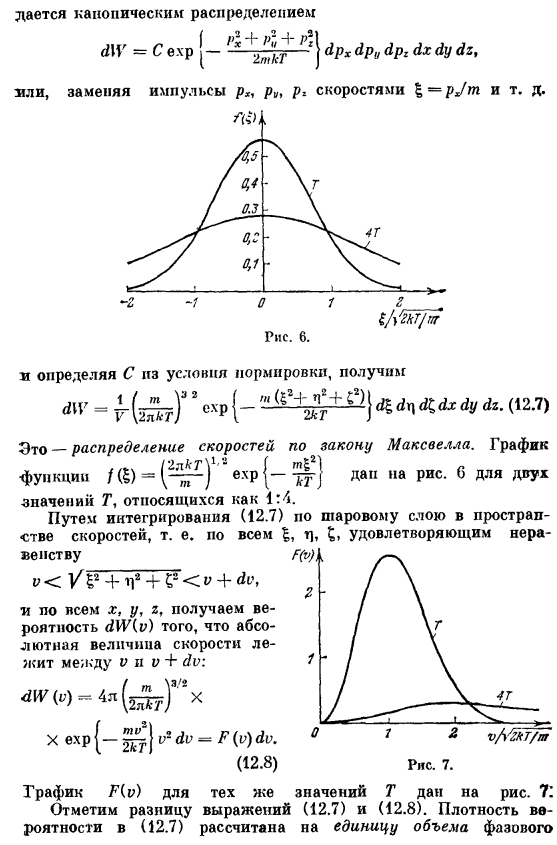
Таким образом, вероятность того, что молекулы имеют импульс и координаты через равные промежутки времени (РЖ, П ’+ П».Пт+ <(п«; пу П> + ДП,-, х, х + ДХ, у, г + ды; з з + ДЗ) Мы окружены нормальным распределением d \ V = c exp замените yali, momentas p «p», p, speed| = pjm и т. д. Около 1 г Т / Дальнем/ м Инжир. Шесть Определите C из условия Нормализация, мы получаем «- рш ’ (- «^ага!»»Т *(12.7) Это распределение скорости по закону Максвелла. На рисунке 1 показано значение T в функции f (5)= (^^) exp {—Tr) dap » A Fig-⁶D» UX. It называется 1: 4. Путем интеграции.
Следующим, более огрубленным уровнем описания является статистическое описание, когда динамические состояния усредняются по ячейкам фазового пространства в классической механике. Людмила Фирмаль
Скорость, то есть вся страна в — (12.8) На сферическом слое прострапа; ’ s 5> Инжир. 7. График F (v) Обратите внимание на различия в (12.7) пианизме Те же значения T показаны на рисунке. 7: формулы(12.7) и (12.8).Плотность BB рассчитывается для каждого единичного объема фазы г = = г]• = £ = 0.Плотность вероятности уравнения (12.8) присваивается интервалу скоростей, равному 1.Поскольку объем слоя сферы в пространстве скоростей становится большим, а V= vₘ = V2kT / m становится большим, а затем уменьшается, он становится большим сначала с увеличением скорости.
Значение vₘ, соответствующее максимальному значению, называется расчетной скоростью. Вы также можете использовать (12.8), чтобы найти среднюю квадратную скорость. Подобный этому Также по курсу Лапласа Средняя квадратная скорость-это просто звук связывания в Газе на некоторое время. Действительно, по формуле / Яг V и М. Где m-молярная масса газа. Н / М-К / М、 V3CjC» а.» Коэффициент теплоемкости КДЖК. Диапазон различных газов составляет 1,2-1.66.Следовательно.)^ o2 и a-величины одного порядка. Средняя квадратная скорость v2 примерно в 1,5 раза больше a. для одноатомного газа C, C составляет 1,66, как видно из $ 17, поэтому для него / «=3а / / б-1.34 а.
Смотрите также:

