Оглавление:




Уравнения Гамильтона. Фазовое пространство
- Как известно из механики, дифференциальные уравнения движения для систем механического обслуживания могут быть описаны в формате Гамильтона. * ДУ’1 Л 、、、 •———…………….. «■»ч Где», P » — обобщенная координата и импульс. Ч(м, р) — ч(qᵤq» …, м,, pₜ, Пи■..А, стр. а.) Гамильтонова функция system. It равна полной энергии системы и выражается в виде функции координат и импульса. Форма этой функции определяется рассматриваемой системой.
Гамильтонова функция связана связана с функцией Лагранжа L в соотношении. Где n-число степеней свободы в системе. Если движение рассматривается в инерциальной системе отсчета, отсутствует магнитное поле, и может быть использован закон нерелятивистской механики (далее мы будем рассматривать этот простейший случай почти исключительно), то функция Гамильтона равна сумме кинетической энергии K и потенциальной энергии u.: Ч-KXq, п)+ щ(щ).
Процесс, при котором не происходит никаких других изменений, кроме передачи теплоты от холодного тела к горячему, называется процессом Клаузиуса. Людмила Фирмаль
Интеграл движения, то есть решение системы дифференциальных уравнений (1.1), можно представить следующим образом: ПК =Ф*(??。Рь0.Як = ф * (?°, ПЛ,0.(1-2) А, 1-1, 2,…. С. С.、 Где q°, p — начальная координата и импульс. Функции q> и φ являются однозначными непрерывными функциями с аргументами q°, p°.Интеграл движения также может быть записан в другой форме. То есть остаток делится на уравнение pₜ—dH /DQ 2n-получаем формулу (1.1) 1, yH/ apt dll! DQ. dpdhdhtdqₙ dpₗiHldq ^ ’ Эта независимая от времени Гамильтонова система Функция не содержит t. существует 2n-1 интегралов, и это число, очевидно, включает в себя, прежде всего, интеграл от анергии ПДД, п) ■ ■ я(д, р)-у-Е.
Далее, Интеграл 2n-2: ПДД, п)=a₂,….Ф «(д, р) — «、 (1.3) (1.5) Ч ’ ДД, п)=₽…. 4fn(г, п)- Здесь… И»; p₂,…, Является интегральной константой. Окончательно. Интеграл можно получить, например, решив следующее уравнение: Используйте (1.4) и (1.5). он имеет форму УДА, р) т+₽,. На самом деле добавление константы к t не нарушает дифференциальное уравнение. т. к. вводится только под символ производной. Для систем с 1 степенью свободы все характеристики решения уравнения движения могут быть легко объяснены графическим изображением на плоскости. Например, рассмотрим движение линейного гармонического осциллятора.
Гамильтонова функция (если масса равна 1) [12]имеет голую*форму. (1.7) Я = 2 (р’+»’? ’)• уравнение Гамильтона * эн 9 = Р = Есть интегралы, которые можно описать как окей. (1-8) Или как Интеграл энергии 2Я-р ’+ » Дд1 = 2å (1.10) И отношение, определяющее временную зависимость p и g: + 0.(1.Я… ) Состояние осциллятора может быть представлено точкой на» фазовой плоскости «q, P. движение системы соответствует движению фазовой точки изображения вдоль»фазовой линии«, определяемой уравнением энергии. Эти кривые постоянной энергии представляют собой систему подобных эллипсов. 2-й Интеграл (1.11)определяет скорость фазовой точки вдоль этой кривой.
Для систем с большим количеством степеней свободы используются аналогичные геометрические термины. если значения q и p считать ортогональными координатами 2-мерного пространства, то состояние системы («фаза») определяется точками («фазовыми точками»или» точками изображения») в этом 2-мерном»фазовом пространстве«.Если система представляет собой отдельную молекулу, то это пространство называется с-пространством, но если это совокупность частиц (газ или другой объект в целом), то G-пространство.
- Со временем точки изображения перемещаются по кривой вдоль «космической траектории» в фазовом пространстве. Эта кривая определяется пересечением 2n-1 «поверхности» (1.4) и (1.5).Поэтому в любом случае она находится на»поверхности энергии». Последний Интеграл (1.7) определяет движение точки изображения. Производные dL и p можно рассматривать как компоненты двумерного вектора»фазовой скорости».Это скорость точки изображения вдоль фазовой траектории. Отметим, что из-за единственности решения уравнения движения 2 различные фазовые траектории не могут пересекаться.
(На самом деле, если это так, начальное положение точки изображения находится на пересечении, то начальное состояние системы определяет, что дальнейшее движение неоднозначно.) Если рассматривать не 1 систему, а всю их совокупность, то состояние определяется множеством фазовых точек, множеством движений и множеством фазовых орбит. Для наглядного представления фазовую точку можно сравнить с множеством частиц, взвешенных в жидкости (или, если они распределены непрерывно, то находятся на своем пределе, вводя в жидкость краску).в этом случае из-за уравнения Гамильтона(Я не зависит от t) поток жидкости необходимо считать стационарным, так как фазовая скорость в данной точке не зависит от времени.
Постулат Клаузиуса: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Людмила Фирмаль
В статистической физике понятие поверхности энергии играет важную роль. Поэтому далее мы приведем примеры на поверхности энергии в простейшем случае. Рассмотрим систему с большим количеством степеней свободы, которая совершает небольшие колебания вокруг равновесия position. As известно из механики, в этом случае»нормальные»координаты всегда found. In эти координаты, гамильтониан Функция выражается как: −2(п * + (1.12) Гдеo » — собственная частота системы. форма уравнения эперги имеет вид (1.13) Это веселый эллипсоид с полуосью e = V2£, wn-G2E / w2n. (1.14)
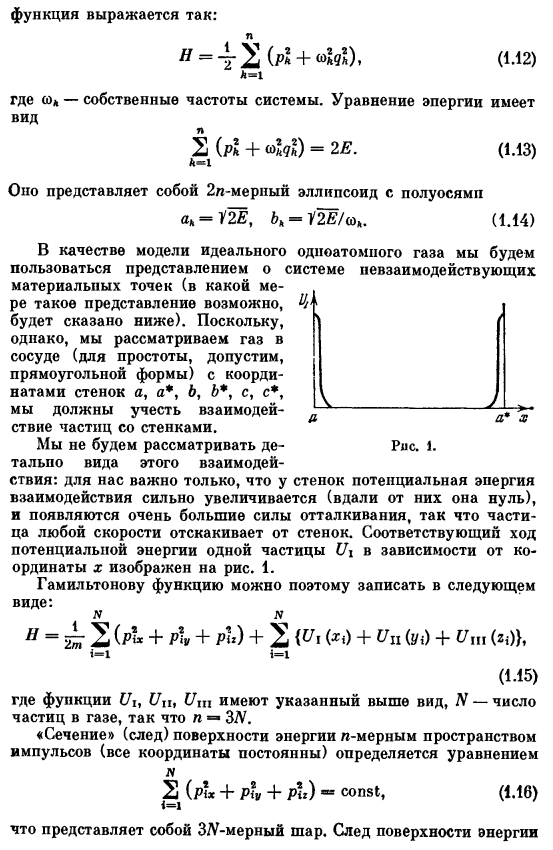
В качестве модели идеального одноатомного газа мы используем понятие системы материальных точек, которые не взаимодействуют (насколько такое представление возможно, мы опишем ниже).Однако необходимо учитывать взаимодействие частиц со стенкой, так как учитывается газ в контейнере с координатами стенок a, a, b, b, c, c *(для простоты, например, прямоугольник). Мы не будем подробно рассматривать эту форму взаимодействия. Действие: для нас важно то, что потенциальная энергия взаимодействия вблизи стенок значительно увеличивается(вдали от них-ноль) и возникает очень большая сила отталкивания, заставляющая частицы любой скорости отскакивать от стенок.
На рис. 1 показан соответствующий ход потенциальной энергии в одной частице Ui В зависимости от координаты x на Рис.5. 1. Поэтому Гамильтонову функцию можно записать следующим образом: I » s-2(A + i + p’«)+ 2 *«)+(p») +(и»、 (1.15) где Uₜ, Un и Uni имеют вид выше, где N-число частиц в газе, поэтому n равно 3N. ■»Поперечное сечение» энергетической поверхности n-мерным пространством импульса (следа) (все координаты постоянны) С(р ’»+ р?»+Р * з)-константный、 (1.16) что такое zlg размерный шар? Поверхностная энергия трассировки.
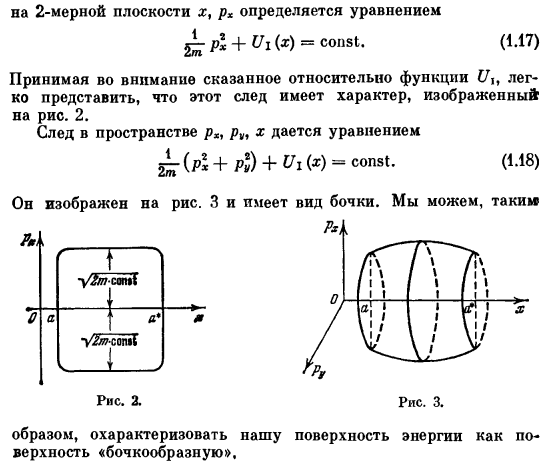
На двумерной плоскости x, p * определяется следующим уравнением: ЛП + ИП(Р)= const и (1.17) Принимая во внимание то, что было сказано о функции U, легко представить, что этот след имеет характеристики, показанные на рисунке. 2. Пространство p » p,, x следы выражения 2 ^ — (₽*+ЛП)+ ИП(х)= const и (1.18) Поэтому она должна характеризовать поверхность нашей энергии как» бочкообразную » поверхность.
Смотрите также:
| Равновесие смеси идеальных газов в поле внешних сил | Теорема Лиувилля |
| Химическое равновесие в смеси идеальных газон | Формальное и физическое понятие вероятности |

