Оглавление:

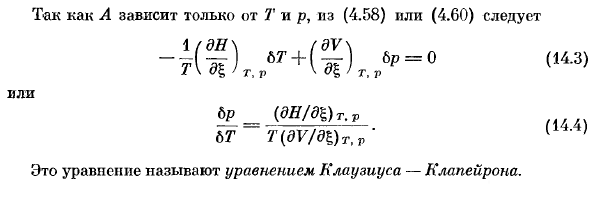



Фазовые превращения. Уравнение Клаузиуса — Клаперона.
- Фазовое преобразование Уравнение карася-клаперон В предыдущей главе было установлено основание очень важного общего закона гетерогенных систем-законов Гиббса и Духема. Здесь мы начнем с изучения фазового перехода чистой материи и более подробно рассмотрим количественные законы, описывающие поведение некоторых простых систем.
Для гетерологичных систем а-0 со смешанной фазой знакомство с условиями термодинамической устойчивости будет рассмотрено в следующей главе. Во-первых, рассмотрим двухфазную однокомпонентную систему. Химический потенциал чистого вещества определяется только температурой и давлением, а также сродством фазового превращения. Равновесное состояние A (7 \ p)= 0, (14.1) Следовательно, конкретное значение либо централизованной переменной T, либо p соответствует конкретному значению другой variable. It базируется на правиле фазы ’(13.5) и такие системы (c = 1, r *-0, φ= 2) являются univariate. So, в координате T-p имеется кривая равновесия A = 0 (рис.14.1).
Дифференциальное уравнение, удовлетворяющее этой кривой, можно легко получить, приняв во внимание, что в случае смещения вдоль аффинности аффинность остается на нуле. Людмила Фирмаль
Это означает, что для любого изменения вдоль этой кривой (14.2) 6А-0. Поскольку A зависит только от T и p, либо (4.58), либо (4.60) Или б п (ду / дБ) т, п (14.4) 6 T T (dV / D l )TtP ’ это уравнение называется уравнением Клаузиуса-крапейрона. Испарение жидкости Когда жидкость или твердое вещество испаряется, потенциал испарения трот Ач по определению равен теплоте реакции он / фаза. (14.4), дайте его для этого (14.5)
- Можно рассчитать уравнения, вращения 6 AEH по Р 6 t TAei ’ Где Aev-изменение молярного объема при испарении. Если предположить, что пар ведет себя как идеальный газ и что молярный объем конденсированной фазы пренебрежимо мал по сравнению с молярным объемом пара, то этому уравнению можно придать простую приближенную форму. И затем… АЕВ =ве-в «КБ *» ВР = R77p,(14.6) Введите (14.5) (14.7) 67 ″ им в」 Кроме того, если предположить, что Deh рассматриваемого диапазона температур не зависит от температуры, Интеграл (14.7) дает приближенное уравнение.
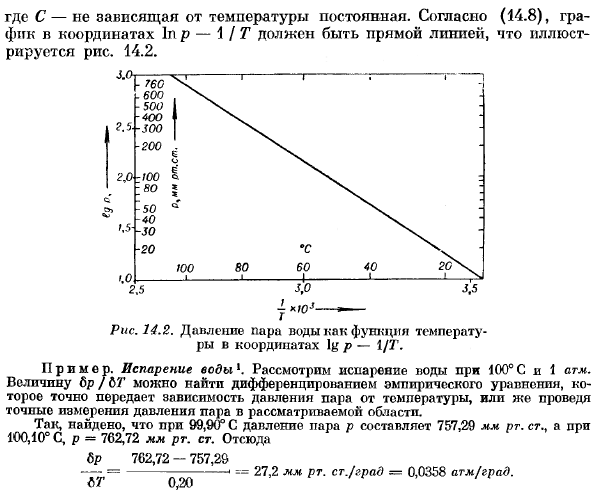
Мешок 1pr = — / £ + с,(14.8) Где C-независимая от температуры константа. Согласно (14.8), график координат в p-1 /Т должен быть прямой линией, как показано на рисунке. 14.2. Рис. 14.2.Координата log P-давление водяного пара в зависимости от температуры 1/7′. Пример. Испарение воды 1. Учитывают испарение пода при 100°С и 1 атм. Значение Lp / Lt может быть найдено путем дифференцирования эмпирической формулы, которая точно передает температурную зависимость давления пара, или путем точного измерения давления пара в рассматриваемой области.
Таким образом, при 99,90°C давление пара p оказалось равным 757,29 мм рт. ст.. И на 100.10°С, Р = 762.72 мм РГ. Искусство. Отсюда 6р 702.72-757.29 —- =- «==27.2 мм рт. Старший / Сити-0.0358 банкомата /банка. L U 0.20 Молярный объем v *и vm при 1 атм и 100°с равны соответственно ВФ = 16.0-1.67 л / моль,^ = 18.0-0.00104 л / моль При подаче заявки (14.8)、 ВР. d eh = GDVU-= 373-0.0358-18.0-1.67 = 401 l-атм / моль = 6 г = 9710 кал / моль — > 50 600 Дж / моль. Прямая калориметрия от 9709 до 9738 кал! Значение, полученное между моль, скорее всего значение 9714 кал! Мол находится в хорошем согласии с результатом расчета.
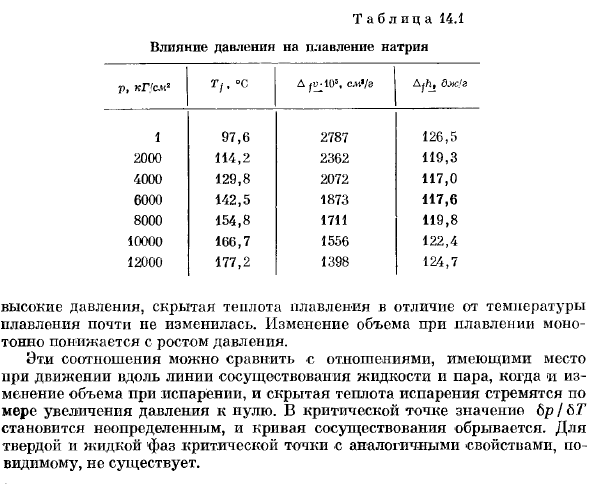
Твердый плавить При рассмотрении температуры плавления твердых тел в зависимости от давления удобнее использовать величину Lt / pa-vnop Tkfv / Afk. Где Afv — изменение объема при плавлении, А D / A-скрытая теплота плавления. Из экспериментальных данных по изменению объема при плавлении и наклона кривой, пл.- Смогите высчитать давление, плавя скрытую жару ФХ. Внутри таблицы. 14.1 приведены результаты аналогичных измерений на натрии(по данным Bridgman1).Несмотря на то, что、 Таблица 14.1 Влияние давления на плавление натрия p, кг ’ см3 Tf. °С Д Сцг.108, С. Н./ с хостела djh, ОЖ.’г’ 1 97.6 2787 126.5 2000 114.2 2362 119.3 4000 129.8 2072 117.0 6000 142.5 1873 117.6 8000 154.8 1711 119.8 10000 166.7 1556 122.4 12000 177.2 1398 124.7 В отличие от температуры плавления, высокое давление, плавление скрытого тепла не сильно изменилось.
Объемные изменения при плавке монотонно уменьшаются с увеличением давления. Эти соотношения можно сравнить с отношениями, возникающими при движении по линиям сосуществования жидкости и пара, когда как изменение объема при испарении, так и скрытая теплота испарения стремятся увеличить давление на projectile. At критическая точка, Lp / b. значение ’/ ’ не определено, и кривая сосуществования нарушена.
Для (твердого и жидкого), по-видимому, нет подобной»критической точки»с аналогичными характеристиками. Людмила Фирмаль
Смотрите также:
Решение задач по термодинамике
| Выбор независимых переменных | Постоянные давления пара и химические постоянные |
| Об азеотропных системах и безразличных состояниях | Давление пара и энтропия испарения |

