Оглавление:



























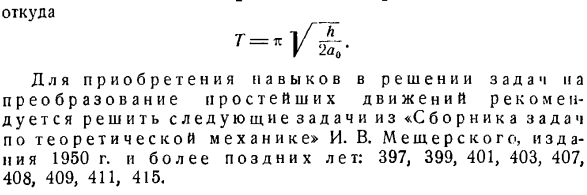

Преобразование простейших движений
- Преобразование простейших движений при преобразовании движения npocrcfiumx, а) преобразовании вращательного движения в поступательное(и наоборот), б)преобразовании 1″вращения вокруг неподвижной оси во вращение вокруг другой неподвижной оси, в) преобразовании постоянного движения и другого перемещения стыка I.
При решении задачи движения механизма преобразования простейших движений необходимо совместно использовать кинематику точек и твердых тел, вращающихся вокруг неподвижной оси. 1 трехмерное вращение вокруг неподвижной оси преобразуется в 2-мерное вращение вокруг другой неподвижной оси с помощью 2-х колесной шестерни или фрикционной передачи (рис. 4.3, а, б) или ременной передачи (рис.4.4, 4.5).
В двигателе внутреннего сгорания используется плоский шатунный коленчатый вал Людмила Фирмаль
Рисунок 4.3. Это модуль скорости точки над ободом шестерни 3 с радиусом RG>, связанным с шестерней//в то же время. Поэтому угловая скорость шестерни 3 и барабана III равна _v_z _vRxR » — Ъ^ ^я• Модуль скорости точки на ободе барабана III радиуса # 3 равен целевому значению скорости груза M и задается следующей формулой: vRtR2R2 Задание 4.44, к 4.15. П2■= у> J, то РС = Р r2ra
Задача 4.14.To преобразование циклического возвратно-поступательного линейного движения во вращательное. коленчатый вал= R, вращающийся вокруг неподвижной точки О в плоскости рисунка, шатун ав = 1, соединенный с коленчатым валом, поршень движется вдоль горизонтальной направляющей цилиндра и совпадает с линейным штоком поршня Ab. он подключен к интернету.
- Установите угловую скорость кривошипа OA на постоянную o0, чтобы определить уравнение движения и скорость поршня B. найдите скорость поршня с 0>, равны <Р-< » 0Л Если опустить перпендикуляры из точки A в прямую OB, то найдем уравнение движения поршня B Х = ОД + ДБ = О Л сов? ± Ади = Р cosw0/ + вл * — Р2 см * я«0т. чтобы определить проекцию скорости поршня B на ось x, необходимо вычислить производную по времени от координат поршня X.
дуплексный. системы r2o)0 грехе 0 > 01 потому что из x «= X—r — — — ГШ0sin Uj-uц = = = R — = 0 до РХ-Р * ИИН * » о * = — ru> 0 [l+, rC0S <^ 1 Sin V. (1) Величина проекции частоты вращения поршня при различных значениях угла поворота коленчатого вала соответствует (1) Значение: СР, — 0 и < Р3-Р ВД = 0,<Р9 = » Р / 2 х = — rr0、 То есть, если 5 [«1 J -; for <Р3 = Т = ру> 5 [1-7]. Задача 4. 16.To для подъема груза Р используется электрическая лебедка, состоящая из приводного вала с шестернями с зубчатым рядом 2 \зубьев.
Когда ведомый вал вращается вместе с шестерней, нагрузка повышается. Людмила Фирмаль
Число зубьев в шестернях < r <в этом случае трос, с помощью которого подвешивается груз Р, наматывается на барабан с радиусом R. уравнение вращения приводного вала、 <П= 2 * Л Определите уравнение движения, скорости и ускорения груза R. Решение. Точка на ободе сцепленной шестерни равна траектории движения, то есть Си = 9iri = ОКР(1) Ш. К задаче 4!! Б. Где rit r9-радиус зубчатых колес I и II, то есть угол поворота ведомого вала. (1) от: Р я. 21 _0- / 2 2 \ -; -.
Проекция скорости движения груза в вертикальном направлении по координатам относительно времени S. Is определяется как производная от 3. В. является> = 4-РТ * Ла с 2 Проекция ускорения груза, который движется линейно в направлении движения, равна производной по времени проекции скорости Зи.
2-й способ solve. As производная угла поворота по времени, определяющая проекцию угловой скорости приводного вала на ось вращения. а) у =?Я = 4. Далее находим значение угловой скорости ведущего вала, исходя из того, что точки соприкосновения обоих колес равны по скорости < ГС г ’ Откуда? 0)Я:= 0> я? Я = 4 ЗТ-Джей. А! Скорость движения груза равна скорости и размеру точек на поверхности барабана Ро> я = 4Р. РТЗ-1-. (2) * 2 Касательное ускорение точки на поверхности б
Ускорение линейно движущейся нагрузки равно по величине тангенциальному ускорению точки на поверхности барабана Чтобы определить уравнение движения груза, запишем уравнение (’2) в виде: Если вы умножите обе стороны уравнения на dU, это выглядит так: ДС = 4zR 1 ДТ. зет. *
От 0 до s. интегрирование в диапазоне j и от 0 до t находит уравнение движения груза M. Си = 2р. Р-Т. \ А. З Во 2-м решении определяются величина угловой скорости ведомого вала и его угловое ускорение. Эти величины характеризуют движение груза а как частный случай, связанный с движением ведомого вала. Поэтому предпочтительнее 2-е решение.
Задача 4. 17.Редуктор, который предназначен для изменения величины угловой скорости при передаче вращения от вала к валу, состоит из 4 шестерен, вращающихся вокруг неподвижной оси. Количество зубьев на зубчатом колесе можно определить по zx= 12 2 * = 72、£3 = l0.Вал II должен иметь скорость 100 об/мин, а вал / — 5400 об / мин. Найдите количество зубьев 4-й передачи.
Разрешение е. угловая скорость первой пары зубчатых колес, совмещенных друг с другом, обратно пропорциональна числу зубьев. К задаче 4.17. _ З2. (2) (1) < 0、 Аналогичное уравнение можно записать для 2-й пары зацепленных колес. * ! =£Т ш,2 Поскольку колеса 2 и 3 прочно закреплены на общем валу, их угловая скорость равна o. Коэффициент смешивания угловой скорости равен отношению количества стаек за 1 минуту. (3) подставляя известные данные, он выглядит так: MOO _ 72 g, » 100 ~ ~ G2•10;
Поэтому в 4-й передаче имеется 90 зубьев. Задача 4. 18.Фрикционная зубчатая передача shaft / Jochy yampee вращается с угловой скоростью, достигая 300 об / мин, и в то же время Двигайтесь в направлении стрелки согласно уравнению и возвращайтесь назад д =(4 4-3 потому что 2ist) см、 Здесь время дается в секундах. Радиус колес: r = 5 см, R = 20 см. 1) угловое ускорение вала II в зависимости от времени, 2) определить ускорение точки на ободе колеса II в момент времени = 0. ^ = ^ 0,25 секунды; ^ s = 0,5 секунды Решение.
Скорость точек соприкосновения обоих колес равна//друг другу, так как колесо / фрикционная шестерня катится без скольжения по колесу. Величина угловой скорости приводного вала В0 = 300 — ^ р — = я ОИК сек (я) О. Колесо I модуль скорости точки обода в контакте с колесом II、 v = hm0 = = 5•1 или = 50 г / с. (2) К задаче 4.18. Значение скорости в этой же точке принадлежит колесу//и равно следующему в = Ш ^,(3) Где co-модуль угловой скорости колеса II. By приравнивая значения (2) и (3), можно увидеть значение II угловой скорости колеса. 50Л ООЯ. 、 Ш === ~~ Г—4 3 потому что 2р. Т, С, Ш•
Проекция углового ускорения колеса II равна производной проекции угловой скорости времени (Предположим, что ось z идет к оси o) Zool’Sin 2nt 300ya’Sin. 、 Внутренние зубчатые передачи (рис.4.3, а) и непересекающиеся ременные передачи (рис. 4.4) соответствуют направлению вращения обоих колес. Если вы используете внешнюю передачу (рис. 4.3, Б) и поперечно-ременную передачу (рис.4.5), направление вращения колес будет изменено на противоположное. Значения скорости ободьев шестерен, которые входят в зацепление, равны.
Скорость модулей и обода одинакова. Если шкив не имеет скольжения ремня, то шкив ременной передачи. Угловая скорость колеса обратно пропорциональна количеству зубьев, радиусу или диаметру Рисунок 4.5. — я- _ Г±_.ти М * Л Рисунок 4-4. Да2 М 21 д \ ’ В этой формуле»> » — модуль угловой скорости, r, r * — радиус начальной окружности, dt> d-I-диаметр начальной окружности, 2], z.3-Число зубьев 1-го и 2-го колес соответственно. Зубчатые колеса, нарисованные на рисунке, и ременная передача 4.3-4.5 являются примерами ряда Соединенных колес и шкивов.
При последовательном подключении каждое колесо вращается вокруг фиксированной оси. Все прошло! Определите точку ускорения на ободе 2-го колеса в разных точках. Во-первых, найти сумму в каждый момент времени: o>, e. выражение(1)、(4)、(5)Вы можете использовать следующую команду * 1 = 0-сек-1%£j-0、 50-й, 75-й. * В т. к.} = 0,25 с с тој ІК = сек’*, Е1 = — сек〜\ Ф = 0,5 с, со3 = 50 сек’1, Е3 = 0 Затем, согласно формуле, определяют значение точки ускорения обода колеса II. ш = Р / Е * + О> 4
. Подставляя значения R, e и co для каждого момента, находим следующее: tx = 0 и\ = 10000 см / с * = 100 м! с. \ в = 0,25 с Ш * = 5 ТФ * й/ 75 * + 625 * см / с * = 308 м! з \ у Т3 = 0,5 с чи)Т = 50 000 т 4 я «495 000 см \ с%= 4950 ЛГ / сла Задача 4. 19.При пуске кулачки начинают вращаться из неподвижного состояния вокруг неподвижной оси O с постоянным угловым ускорением e = 0,1 g сек.* при достижении кулачками угловой скорости, соответствующей 40 об / мин, они вращаются более равномерно. Форма уравнения контура кулачка-y / / / / / l. Р = (]) * ВТМ (Спираль Архимеда).
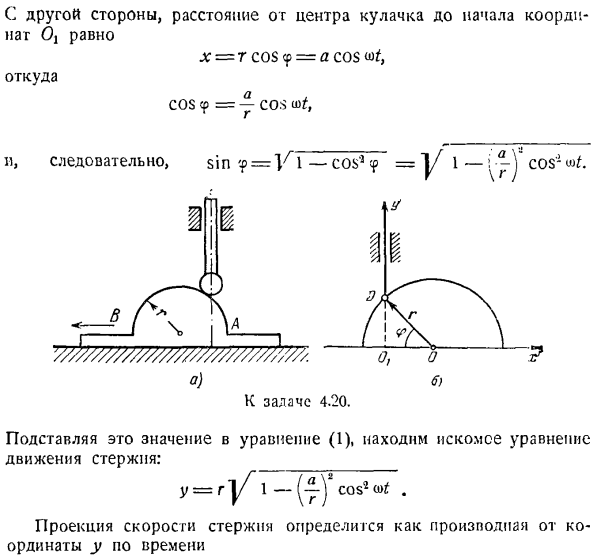
Вал кулачкового механизма а перемещается к задаче 4 19. Закреплены Направляющие Б Как показано на рисунке, контактируйте контур кулачка с пружиной. Определите скорость Поскольку стержень движется по прямой, проекция скорости на ось x будет равна производной по времени от координаты G. данные = Р〜2-1.5 * = 3 * см / с (4)
Проекция ускорения стержня, движущегося по прямой, равна производной по времени проекции скорости wx = vx = 3 см}секунд(5) В зависимости от условий, при достижении угловой скорости, соответствующей 40 об / мин, кулачок вращается еще более равномерно. Модуль угловой скорости последующего равномерного вращения кулачка (О1 = = 40г = л.(6) Если вы дифференцируете по времени(1), Вы найдете проекцию скорости стержня на ось X. 30. 30 30 4,… = » = — ?= = = см] секунд (7)
Загрузка продолжается до тех пор, пока скорость(4)не станет равной vxi. Сравним эти 2 значения скорости и определим время пуска T ЗГ = 40 или 7 = 13,33 секунды (8) Время начала можно определить и другим способом. Проекция угловой скорости кулачка при запуске определяется как производная по времени от угла поворота (2) о. >. = 6 = 0.1 Тл. (9) Для определения времени начала T величина проекции угловой скорости (9) равна ее значению (G).И затем… Или 7 = 13,33 секунды. О
Задание 4.20.Круговой прогрессивный подвижный кулачок перемещается в соответствии с уравнением (рисунок а). x = A cos » tf、 координата x измеряется в горизонтальном направлении от точки 0| (рисунок b), где a, w-постоянные коэффициенты, а t-время. Определите уравнение движения и скорость стержня. Решение. Введите угол o, как показано на рисунке. b, найти координаты дна стержня(рисунок b) 0.) г = р грех <п. С другой стороны, расстояние og от центра кулачка до начала координат Oh равно X = 7 COS
При подъеме груза трос оборачивается вокруг барабана B и вращается вокруг неподвижного вала O. Скорость и ускорение (радиус R) точки на ободе барабана, значение постоянной a0, общее время подъема груза, а также Момент, когда угловое и угловое ускорение барабана достигает максимального и минимального значений. Решение.
Величина скорости точки на ободе барабана равна модулю скорости подъема груза. Проекция скорости груза равна производной по времени от координаты Y Г-Ш3. Так… 4. 21 к проблеме. вы = Р = — J, его грех <Р Здесь.、/ 7 = 0、1、2、3、4、…Подставляя значение < p из (2) в (4), находим момент времени, соответствующий максимальному значению абсолютной величины угловой скорости. Тю+ -) / £• Точки же времени соответствуют вращению от углового ускорения барабана к пуле, то есть минимальному коэффициенту углового ускорения.
Абсолютное значение коэффициента угловой скорости равно sin cpz = 0 Следовательно、 Ч * =(5) Здесь, н= 0、1、2、3、4、…Подставляя значение угла (5) (2), вы найдете моменты времени, соответствующие минимальному значению модуля. Угловая скорость Из V Этот же момент времени соответствует наибольшему значению коэффициента углового ускорения. Нормальное ускорение точки на ободе барабана wn-u1R = A£ — / j sin2 <p.
Проекция ускорения этой точки На касательную серии WX = e2R = Ак, потому что кф. Эта формула одновременно определяет проекцию ускорения нагрузки на ось Y. Поэтому константа А0 является максимальным значением ускорения нагрузки. Максимальное ускорение точки на ободе равно в = ОВВ + интернет Wi-А0] / «sin4 <п + потому что» <С. Направление ускорения определяется уравнением радиуса и угла a ж я, 2Г, потому что 9 б шя УР ч sin2 <Р *
Общее время нарастания T определяется из равенства(1).если вы используете h вместо y и его значение (2) вместо<p、 а = а [, _ C0S г ^ т]. Откуда? Для овладения навыками решения задач и преобразования простейших движений теория механики И. В. Мещерского представляет собой сборник задач, рекомендованных для решения следующих задач начиная с изданий 1950-х годов:397、399、401、403、407、408 、409、411、415。
Общее время нарастания T определяется из равенства(1).если вы используете h вместо y и его значение (2) вместо<p、 а = а [, _ C0S г ^ т]. Откуда? Для овладения навыками решения задач и преобразования простейших движений теория механики И. В. Мещерского представляет собой сборник задач, рекомендованных для решения следующих задач начиная с изданий 1950-х годов:397、399、401、403、407、408 、409、411、415。
Параллельное соединение колес часто используется, когда 2 колеса вращаются вокруг 1 неподвижного axis. At при этом, если они плотно соединены друг с другом, их угловые скорости будут равны. При решении задач, связанных с преобразованием простых движений, рекомендуется следующая последовательность действий: 1) исходя из условия задачи, движение описывается известным уравнением движения твердого тела или другой кинематической связью.
2) используя уравнение движения твердого тела вокруг кинематики точки и неподвижной оси, найти уравнение движения другого твердого тела и найти скорость и ускорение различных точек этого твердого тела, в которых передается движение. Задача 4. 10.Шестерня/находится на внешней передаче с шестерней II. диаметр первого колеса составляет 400 мм, вращающегося вокруг неподвижной оси Au с угловой скоростью o> A = ^ sec1. Если диаметр Di = 320 мм и вращается вокруг неподвижного вала 0,2, определите угловую скорость 2-го колеса. The solution. At точка соприкосновения зубьев обоих колес, точка скорости 1-го и 2-го колес одинаковы.
Значение этой скорости v равно: Д.、 англ Следовательно、 «> , _ Д ^ И если вы используете формулу Dx *(1), Вы можете увидеть следующее: U) Сторона. Колеса Я К задаче 4.1! C0, P, _n. 400, 5. = Считанные секунды 320. В виду того что колесо в внешней передаче, угол Колесо / / вращается по часовой стрелке, потому что скорость меняется против часовой стрелки. Задание 4.11.Шестерня/находится во внутреннем зубчатом кольце с шестерней II. радиус первого колеса равен ri = 150 мм, и оно вращается вокруг неподвижной оси Ot до n {=1500 об / мин.
Если необходимо вращаться вокруг неподвижной оси O, определите радиус 2-го колеса и сделайте его n = 4500 об / мин. Решение. Контактная информация В Задаче 4.10 Точка скорости передачи является первой И 2-е колесо должно быть равным. Значение скорости точки обода колеса / Я< / \ Т> = / Йи>,= Р, — ый. (1) Коэффициент скорости точки обода колеса II г = ГМ = Р ^ ..(2) Если мы сравним равенство (1) и равенство (2), то увидим, что: Дж Г О а _ оч Г2<»»! Р1 ′ «Показывает, как величина угловой скорости пропорциональна числу оборотов в 1 минуту. р,= р, 150 н.
Для этого внутреннего кольца шестерни, обе шестерни вращают в таком же направлении. 4.12.Сцепное устройство с шестерней радиусом g / шестерней радиусом r В настоящее время первое колесо вращается с угловой скоростью = g, и>,= gl21% 1500 4500 = 50 мм. Бросать вызов Ницца. Задача 4. 12. Откуда? Угловая скорость 2-го колеса с внешним зубчатым колесомприспособленную безопасно
. Шестерня соединена с шестерней 2 шестерни / радиуса r и вращается как шестерня II радиуса R, так и блок. Последний склеивается с шестерней 3 радиуса ha и вращается как единое целое с барабаном радиуса III. Если оси всех шестерен неподвижны, то определяют скорость, с которой опускается груз М.
Определение: модуль скорости точки на ободе штанги-цистерны 1 радиуса SPI r равен значению вопроса 4.13. Значение скорости каната точки v. определить скорость точек на ободе зубчатых колес I радиуса RT. барабана 7 и модуля угловой скорости зубчатого колеса С Ш Я _ в、— Значение скорости точки в зубчатом ходу/ в. В] = СО, к= — РЖ. Р 1 Так как шестерни / зацепляются с шестернями радиуса r9 2, то скорости точек на ободах этих колес будут равны. Определите модуль
Смотрите также:
Предмет теоретическая механика

