Оглавление:







Теплоотдача в разреженных газах
- При большом разрежении или низкой плотности газ не сможет считаться сплошной средой (кохиниум), поэтому нельзя определить трение и теплообмен, применив полученную зависимость во всех предыдущих разделах. В разбавленном газе средняя статистическая длина среднего свободного пробега отдельных молекул при 2 столкновениях с другими молекулами, Z, сопоставима с размером сосуда, в котором находится газ located. As в результате величина I начинает влиять на физические процессы, происходящие в Газе.
На основе кинематики и экспериментов получена следующая зависимость: Определить коэффициент вязкости благородного газа Олеер / 、 、 、 (A-172) Заметим, что где и-средняя молекулярная скорость (1-21), произведение plₜ при умеренном давлении остается постоянным, то есть не зависит от давления. Для определения теплопроводности газа из одноатомной молекулы(1-25) (А-173) Где с » — молярная теплоемкость при постоянном объеме. Сажа от сложного ребенка (1-24, 1-25) Х = — ^ — (9к-5).наркомюстом (Некоторые-174) Разделим обе стороны (Сиань-174) на произведение PC ’ B, после преобразования получим формулу для определения критерия Прандтля. Пиар.= (Некоторые-175).
Полная энергия отраженных молекул в реальных условиях . Людмила Фирмаль
Поэтому коэффициент вязкости q и теплопроводность X, которые являются важными физическими константами газа, зависят от среднего свободного пробега молекулы, поэтому это количество также влияет на теплообмен. Этот процесс также зависит от характеристики Izu этого i. совместное влияние этих величин (т / ч, Ф) на теплообмен разреженных газов лучше всего оценивается отношением КН= -^ -. 。Это называется критерием Кнудсена Рассматриваемый критерий Рейнольдса (XY72) определяется по формуле Рэ=(А-177) (Некоторые-176) Где W-макроскопическая скорость .
Может представлять критерий Маха (1-21) и скорость звука (Х1-2) для учета (XL-178) Теперь вы можете выразить критерий Кнудсена через критерий Маха 。Рейнольдс (Некоторые-176), (A-177) и (XI-178 )、 М «. Г. Критерий Кнудсена также может быть выражен следующим соотношением: (Некоторые-179) (Некоторые-180) 6-толщина границы, где、 Соотношение между КН (Сиань-176) и (Си-180), учитывая (в-179).Формат выглядит следующим образом (Некоторые-181) Knₑs В. 6 Король Ранее приобретенные зависимости(в VII-7) (Некоторые-182).
(Некоторые-183) Л-Л-Л-Л-Л-Л-Л-Л-Л-Л-Л、 Ширина пограничного слоя 6 теперь сопоставима с характерным размером тела/. другими словами, поскольку он гамма » 1, (а-182)равен К Для очень больших чисел Рейнольдса уравнение (Сиань-182) принимает следующий вид, учитывая (ви1-8): в- Когда разреженный газ вращается вокруг, наблюдается глубокий эффект. Поэтому расход не исчезает в неподвижной стенке, а газ «скользит» по ней, не «прилипая» к поверхности, как это происходит в непрерывном потоке. Температура газа стенки не равна температуре самой стенки, как это обычно бывает при непрерывном flow. In другими словами,.
На поверхности между стенкой и расположенным рядом с ней слоем газа наблюдается скачок температуры Случай течения, в котором наблюдается описанный эффект. Если средний свободный путь Z становится значительно больше характерного размера тела I, и происходит столкновение тела с молекулой, то в случае течения в условиях очень больших редких условий получить свободный путь невозможно. гораздо чаще, чем столкновения между молекулами, называемыми п e Границы перечисленных режимов течения определяются соотношением (Сиань-183) в.
Снова. Область непрерывного течения, работа которой определяется законом газовой динамики, существует в следующих случаях: / Й Присутствовать в ассортименте — >0,01. Снова. Переходная область между режимом скользящего потока и свободномолекулярным потоком находится в диапазоне 10> — > 0,1. Снова. 7- — >- >Существует для 10. Снова. На практике, например, если сфера диаметром d≈0,3 м движется на высоте 30 ≈ 50 км от Земли, а свободное молекулярное течение может возникать, если ячейка находится на расстоянии более 130 км.
- Это означает, что искусственные спутники, как правило, омываются свободными молекулярными токами в течение периода вокруг .Земли, а на орбите непрерывно омываются потоком непрерывных, движущихся, переходных и свободных молекулярных токов. Тепловой поток от газа к стенке (или наоборот) зависит от коэффициента регулирования, который является следующим соотношением. а) идеал одного атома (Некоторые-184) Какова степень стресса?
Эта молекула попадает на поверхность тела.; Температура поверхности; t-температура газа, которая отражается от поверхности тела после столкновения молекул с телом в случае многоатомного реального газа формула (Сиань-184) оказалась неуместной, поскольку сложные молекулы могут нести не только кинетическую энергию, прямо пропорциональную абсолютной температуре, но и внутреннюю (например, колебательное движение атомов в молекуле). (Некоторые-185.
Молекулы, которые являются предполагается, что они не встречаются с другими молекулами, составляющими газ, который путешествует по организму. Людмила Фирмаль
) Где е-полная энергия (кинетическая энергия и внутренняя энергия) молекул, сталкивающихся с поверхностью тела. E — полная энергия отраженной молекулы, когда температура газа, содержащегося в молекуле, равна температуре стенки. РП. Коэффициент термической адаптации а зависит от материала и качества поверхности. Теперь кратко рассмотрим процесс теплообмена в скользящем и свободном молекулярном потоке regions. It следует отметить, что этот процесс до сих пор не изучен практически теоретически и экспериментально.
Тепловыделение в режиме потока slinto 。Рассмотрим простой случай теплопередачи пластины в области скользящего потока (это решается методом кокерта). Он использовал решение, данное Рэлеем для пластины, которая была потрясающе запущена в непрерывном потоке, но рассмотрела эффект скольжения в граничных условиях. Уравнение Навье-Стокса для такой задачи (Р-29 и P-30) используется, когда пластина движется с постоянной скоростью wₓ.Может быть упрощен поток 2-D, без= = 0, игнорирует члены и возвращает из уравнения St Стокс (11-29) выпуск самолета (Некоторые-186).
Поскольку пластина движется только в направлении x, форма формулы (второй-30) имеет вид (Некоторые-186)из 1 является следующим вы можете сажи. Следовательно Уравнение (XI-186) можно взять из сажи. (Некоторые-187) Граничные условия пластин следующие: 1) Оставайтесь пластиной не первый момент A> 0; 2) через некоторое время после того, как пластина начинает двигаться, скорость газа wₓ на поверхности пластины не равна скорости самой пластины. Если все молекулы являются зеркальными, предположим, что скорость газа на стенке пропорциональна градиенту скорости: > 0.
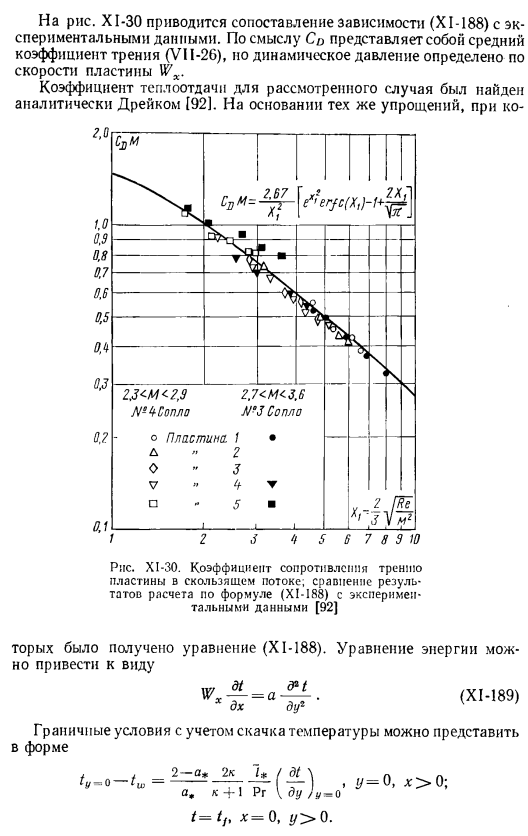
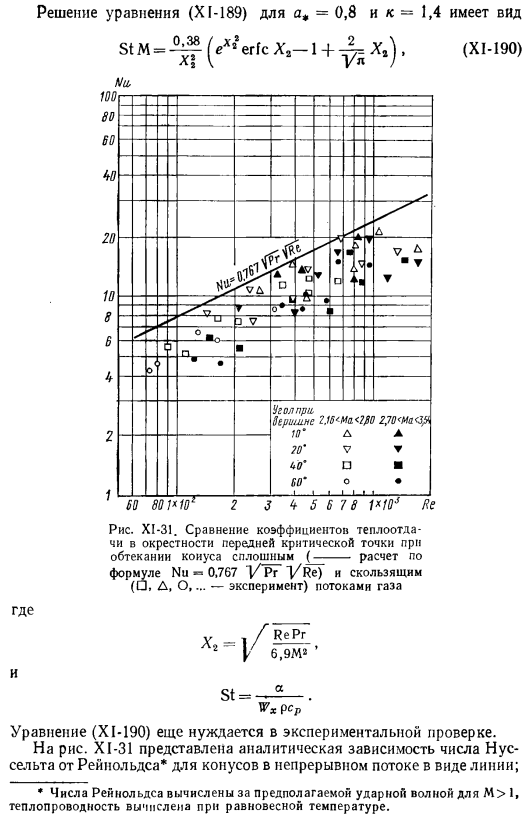
Форма решения граничных условий(1)и(2) (Сиань-187) имеет вид [921 Где CD-коэффициент сопротивления. Определяется как отношение длины I и сопротивления 2 сторон пластины, ширина которой равна 1 к величине erfcX,= — эрф х,. Зависимость (некоторые −188) и эквалайзер correlation. In ко, он плоский. О коэффициентах спермы «северный? На юге страны произошел инцидент. Я нашел упрощение. «■Х1 -, ⁸⁹ ⁾ Можно представить граничные условия, учитывающие скачки температуры * = 0. Г> 0. a, = 0.8 kk = 1.4 уравнения (X1-189) уравнение имеет вид: СТМ » ч «»1’1+ви*■)’ (Некоторые-190) Куда? Выражение (XI-190) должно быть тщательно проверено. На рисунке XI в 31 показана зависимость анализа числа нуссельта от числа .
Рейнольдса * конусов в непрерывном потоке в виде линии. * Если М> 1, то число Рейнольдса вычисляется за ожидаемой ударной волной, а теплопроводность вычисляется при равновесной температуре. Настенная крыса. Теплопередача Малыш! Такой режим течения наблюдается с очень большой редкостью. Свободный путь молекулы свыше 1 знака — к липам. Существует характерный размер тела в этом вопросе определяется следующим образом. Вычислите энергию (поглощение, вращение, вибрацию) молекулы、 ?
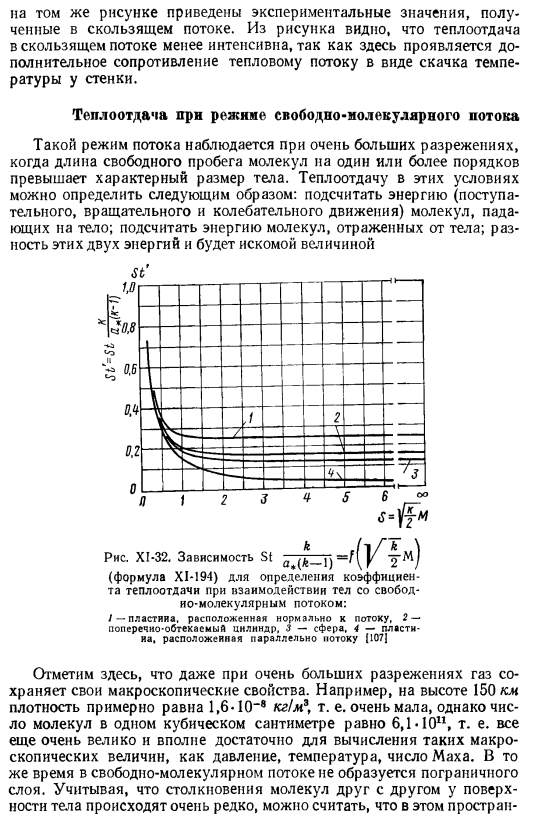
Это достаточно большое значение, чтобы вычислить значение мака I, такое как давление, температура и число Маха. Flow flow поток свободных молекул — да. ….. Тело идет Я пространство Закон распределения скоростей молекул, сформулированный Максвелл (16), продолжает оставаться в силе. Такая ситуация позволяет рассчитать теплообмен на основе законов кинетической теории газов. Полезно выразить уравнение для определения коэффициента теплопередачи в терминах числа Стэнтона St. (Х1-191) И поправочный коэффициент Кин = ф£±л, (А-192) Где G-коэффициент восстановления(а-5).
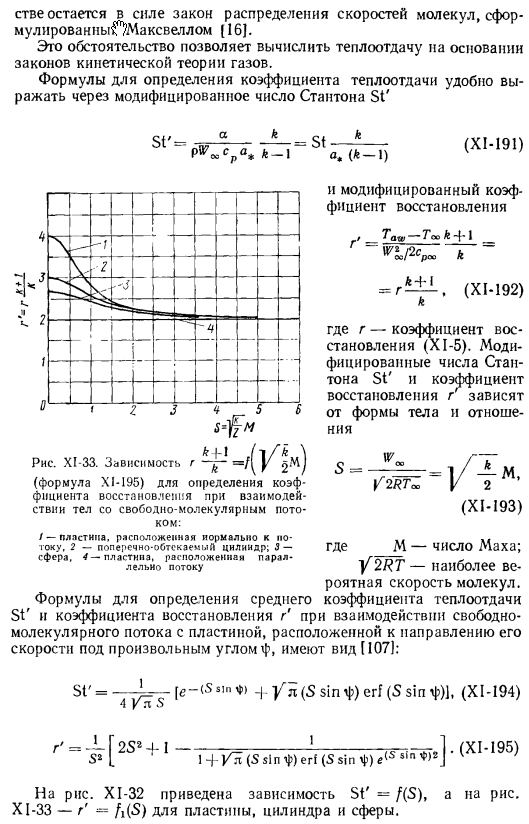
Модифицированное число Стэнтона St ’ и коэффициент восстановления g, относительно формы тела «ЕДИНОЕ ВРЕМЯ _ 1 /-*- M, K 2YAT » 2 (Некоторые-193) M — это число Маха. Y2RT в наиболее вероятная молекулярная скорость, коэффициент теплопередачи Формула для определения среднего значения_ -.«_ _ St ’и коэффициент восстановления g’ при взаимодействии свободного молекулярного потока с пластиной, расположенной под произвольным углом φ в направлении скорости, имеет вид (107). Ст’-₄^ₛ[е-Ц «и» т> +у’л(с sinф)мудрость(с sinф)1.(Некоторые-194) r ’ = [2Sⁱ+ 1 ———- = ————!——— — 11гзг.1 * (A-195) На рисунке XI в 32 показаны зависимости St, ’ = /©, на рисунке XI-33-R ’= В © пластины, цилиндра, сферы).

