Оглавление:













Тепло и массообмен с химическими реакциями в диссоциированном газе
- Если объект взаимодействует с потоком горячего газа (Т> 3000°К), то необходимо учитывать влияние диссоциации на теплообмен. Такое состояние может возникнуть, например, в клетке Ракетный двигатель горит и сопло, или если вы летите на очень высокой скорости. Если самолет летит с большой скоростью (М> 10), то температура перед головкой .
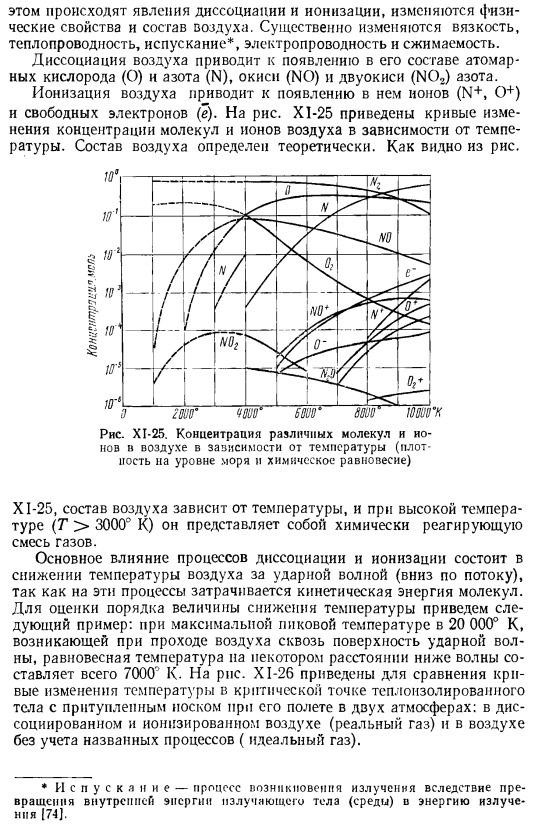
Он достигает очень высоких значений, при этом физические свойства и состав воздуха меняются, при этом происходят явления диссоциации и ионизации. Вязкость значительно меняется Теплопроводность, эмиссия*, электропроводность и сжимаемость. Диссоциация воздуха вызывает появление в его составе атомарного кислорода(O) и азота (N), оксида (NO) и диоксида (NO₂). Азот. Ионизация воздуха приводит к появлению в нем ионов (N+, О) и свободных электронов (e).На рисунке XI-25 показана кривая в зависимости от изменения концентрации молекул и ионов воздуха От температуры.
Концепция локального равновесия заключается в том, что равновесные термодинамические соотношения справедливы для термодинамических переменных, определённых в элементарном объёме, то есть рассматриваемая система может быть мысленно разделена в пространстве. Людмила Фирмаль
Состав воздуха определяется theoretically. As как видно из рис. XI-25.Температурно-зависимая концентрация различных молекул и ионов в воздухе( Море и химическое равновесие) XI-25, состав воздуха зависит от температуры, высокой температуры (G> 3000°K), представляет собой смесь химически реагирующих газов. Главный Поскольку кинетическая энергия молекул расходуется на эти процессы, эффекты процессов диссоциации и ионизации заключаются в понижении температуры воздуха за ударной волной (вниз по течению).
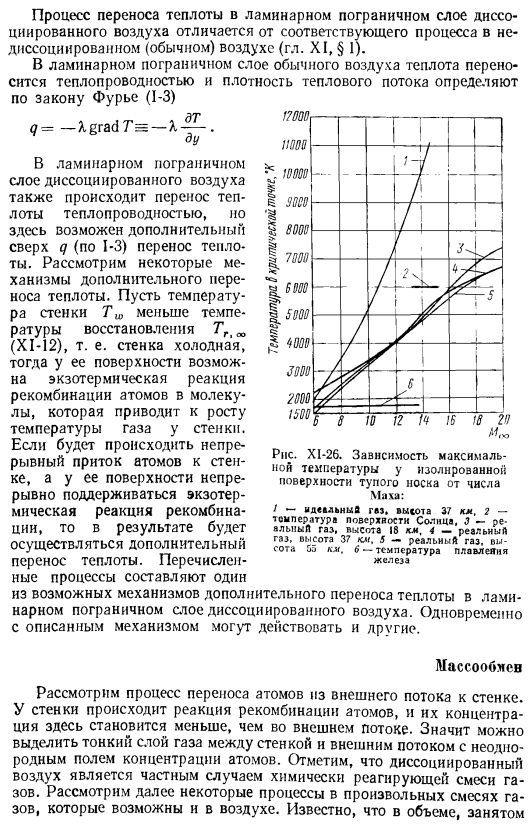
Для оценки степени падения температуры показан следующий пример: максимальная пиковая температура, возникающая при прохождении воздуха через ударную поверхность при 20 000 ° к Равновесная температура на определенном расстоянии ниже волны составляет всего 7000 К-на рисунке XI-26 показана кривая для сравнения изменения температуры в критической точке 2. Теплоизоляция с тупым носом при полете в атмосфере: диссоциированный и ионизированный воздух (реальный газ) и в воздухе без учета вышеуказанных процессов( Идеальный газ.)
Излучение — это процесс, при котором излучение возникает за счет преобразования внутренней энергии излучателя (среды) в лучистую энергию[74].Температура Изолированная поверхность носка тупая от числа Маха:1-идеальный газ, высота 37 км, 2-температура поверхности Солнца.? — Реальный газ, высота 18 км, 4-реальный газ, высота 37 5 км-реальный газ. Высота 55 км. 6-температура плавления железа. Процесс теплообмена в ламинарном пограничном слое диссоциированного воздуха отличается от соответствующего Обработка неразделенным (нормальным) воздухом (XI Глава,§ 1).
в ламинарном пограничном слое нормального воздуха тепло передается за счет теплопроводности и плотности теплового потока Определяется законом Фурье (1-3) a =-A. град T =-1. 5 /в ламинарном пограничном слое диссоциированного воздуха передача тепла также происходит за счет теплопроводности, это возможно здесь теплопередача, превышающая q (1-3).Рассмотрим некоторые механизмы дополнительного теплообмена.
Понизьте температуру стенки Tw, чтобы понизить температуру восстановления₁₁». (XI-12), то есть когда стенка холодная, на ее поверхности происходит экзотермическая реакция рекомбинации атомов в молекулы, что приводит к повышению температуры газа вблизи стенки. Если есть Происходит непрерывный приток атомов к стенке, на ее поверхности непрерывно поддерживается экзотермическая реакция рекомбинации, в результате чего образуется дополнительная Теплопередача.
Эти процессы представляют собой один из возможных механизмов дополнительного теплообмена в ламинарном пограничном слое диссоциированного воздуха. И в то же время Другие могут действовать по объясненному механизму. Массообмен рассмотрим процесс переноса атомов из внешнего потока в wall. In на стенке происходит реакция рекомбинации атомов, которая Концентрация здесь ниже, чем во внешнем потоке. Это означает, что тонкий слой газа можно различить между стенкой с неоднородным полем атомной концентрации и внешним потоком.
Пожалуйста, обратите внимание Диссоциированный воздух является частным случаем смеси химически реагирующих веществ gases. In кроме того, мы рассмотрим несколько процессов с любыми газовыми смесями. Это также возможно в воздухе. Известно, что в объеме, занимаемом смесью газов с неоднородным концентрационным полем компонента, масса этого компонента самопроизвольно перемещается из области, где он расположен.
Концентрация высока в области где концентрация low. In в нашем случае концентрация атомов вблизи стенки невелика, поэтому они перемещаются от внешнего потока к стенке, а концентрация молекул равна Далее они перемещаются от стены к внешнему потоку. Когда поле концентрации становится однородным, движение мелких частиц прекращается. Спонтанный необратимый процесс Массоперенос определенных компонентов в пространстве, в простейшем случае концентрация или парциальное давление неоднородного поля этого компонента называется массопереносом.
Массоперенос Он может быть молекулярным или конвективным. Тепловое движение частиц в смеси веществ называется молекулярной диффузией. Молекулярная диффузия путем Неравномерное распределение концентрации компонентов смеси называется концентрационной диффузией. Конвективный перенос вещества и Конвективный массоперенос называют молекулярной диффузией. Тонкий слой газа. Концентрация этого компонента в смеси характеризуется большим боковым уклоном.
Боковое перемещение этой составляющей происходит (градиент) диффузного пограничного слоя, называемого[74].Может быть градиент концентрации через пограничный слой Не только в результате рекомбинации атомов в молекулы вблизи стенки, но и по другим причинам. Давайте рассмотрим некоторые из них them. To химически активируйте материал стены、 Реагируя с 1 из компонентов газовой смеси-это приводит к снижению концентрации этого компонента в стенках и развитию градиента концентрации. Пожалуйста, подумайте еще об одном.
Случай. Материал стенок химически нейтрален, чтобы не вступать в реакцию с компонентами смешанного газа. Однако в самом пограничном слое химическое вещество Реакция между отдельными компонентами. Предположим, что один из компонентов смеси вступает в реакцию с другим, и концентрация уменьшается по мере приближения wall. In эти условия Градиенты концентрации также occur. In в обоих случаях градиент концентрации определяет массовый расход этого компонента на стенку.
Температура внешнего потока Когда G, температура стенки выше, чем Tw, массовый поток из-за концентрации диффузии передает тепло от внешнего потока к wall. So вы можете объяснить 1 вещь Возможные механизмы дополнительного теплообмена в пограничном слое химического реакционного газа. Далее обратимся к описанию того, как определить величину диффузного потока. Месса. Плотность массового потока при концентрационной диффузии, то есть массовый диффузионный поток количества материала, перемещенного из единицы площади в единицу времени (масса кг).
Определяемый по закону Фика, может быть выражен в следующем виде:/ = — Dgradp ₍=- D -^* -, (XI-129) D-коэффициент диффузии, физическая постоянная. pₜ-концентрация Диффузное вещество / компонент смеси. Размер соответствует местной плотности. Ламинарный пограничный слой газовой смеси в общем случае представляет собой химическую реакцию Работают как температурные, так и концентрационные градиенты компонентов. Поэтому необходимо учитывать законы Фурье и Фика вместе взятые.
Прежде всего, эти законы являются Формы (1-3) и (X1-129) могут быть использованы для ограниченного числа процессов тепломассообмена. Согласно закону Фурье, можно определить молекулярный теплообмен, вызванный Температурные градиенты только в стационарных условиях. По закону Фика можно определить молекулярно-массовый перенос компонентов газовой смеси с помощью градиента концентрации смеси.
Вообще не двигается. Если средний свободный путь молекул больше характерного размера обтекаемого тела, то оба закона не могут быть применены к условиям очень низкой плотности газа. Закон Фурье справедлив для жидкостей с однородными полями концентрации. Как определить тепловой поток пограничного слоя с градиентом с градиентом температуры Концентрируясь, формула закона Фурье (1-3) должна быть дополнена членами, учитывающими дополнительное тепло transfer. In в будущем исследовании мы ограничим наших членов до 1 человека. Учитывают диффузию теплопередачи. Механизм такой передачи описан выше.
- Закон фика справедлив для однородных температурных полей (изотермических жидкостей). Процесс) в условиях независимой диффузии. Независимые условия диффузии наблюдаются в каждом из следующих случаев: смесь состоит только из 2 компонентов или 1 диффузионного компонента、 Смесь определенных составов; диффузионные процессы, протекающие в этих условиях, называются бинарными d и fuses и E. один из процентов(пример: объем) Компоненты крупнее по сравнению с другими компонентами, а поле концентрации в смеси однородно.
Классическая неравновесная термодинамика основана на фундаментальном предположении о локальном равновесии (И. Р. Пригожин, 1947). Людмила Фирмаль
Коэффициент диффузии всех компонентов смеси равен друг другу в 1841 году. В условиях многокомпонентных реакционных смесей происходит взаимодействие теплового потока и диффузионного потока. Тепловой поток и задача определения всех теоретических Диффузия очень сложна, не всегда разрешима. Будущие исследования будут использовать предположение, что двоичный спред может произойти Многокомпонентная смесь. Для этого разделите все микрочастицы смеси на 2 сорта-легкие и тяжелые. Бинарная смесь имеет общий коэффициент диффузии Dᵢ2-D2₁ 1.
Следующий Для анализа процессов тепломассообмена между газами и твердыми телами используется система пограничных слоев. Уравнение сжимаемого ламинарного течения Пограничный слой химической реакции газ XI-27, пограничный слой полон ударов при обтекании тупым носком: / — ударная волна. 2-жесткий слой. 3-пограничный слой Здесь мы обозначим систему названных уравнений. Вывод этих уравнений описан в специальной литературе[16, 27].Уравнение движения в проекции на направление s (рисунок XI-27) (Си-17).
Ни химические реакции, ни диссоциация не дают импульса, поэтому dw₉. dwₛdr. ds и do ds + v (1 ′» HIZO⁾и проекция на ось y (см. Рисунок XI-27) Получаем^ = 0, P = Pn, согласно (X1-17). (XI-131) do q (pa>), q (rsh) Q ds’du (XI-18) (XI-132) напишите непрерывное уравнение смеси на основе Z-го уравнения сохранения массы Форма компонента — «V (р ⁺»⁽ ⁺ ⁾).З здесь?₁₂ — Бинарный коэффициент диффузии. Cₜ-ст / п-относительная концентрация I-го компонента. wₜ-скорость массопереноса t-го компонента. Единичный объем, или падение / го компонента. При химическом превращении общая масса реагирующего вещества не изменяется, следовательно 2(0 /-0.(XI-134).
Уравнение состояния. Р = 2jPi ^ П /?Cm⁷’; / парциальное давление компонента определяется по формуле P, = Pi-T(XI-135).Где k-постоянная Больцмана. mₜ-масса молекулы компонента I-ro. Уравнение энергии. EQUATION3 Equation уравнение энергии (XI-136) и уравнение энергии (XI-19), сравните последнее srdt DH для замены. Это сравнение показывает, что появился новый (XI-136) Период (3-й справа), рассмотрим теплообмен путем диффузии. Уравнение энергии q! Его можно выразить в другой форме:, ROW, — di ddu do 1 Rg do 1 ^ 8 I 2 dI 1 iThₜ^cₚ dT + h] \ b1 (XI-137) (XI-138) (XI-139) (XI-140) A?
Теплота образования i-го компонента при температуре 0 ° К. С | 1 в Pg = — = — число pr. (Си-141) Ле= ПД | АКП-Ф- — \ 1 — это число Льюиса. (X1-142) l. In приведенное выше уравнение, p = p (Cp7), X = X(Cp7), D₁₂==D₁ (T) и P = API (s).Сравните уравнение энергии (XI-137) с уравнением энергии (XI-22).Сравнение Показано, что появился новый термин (XI-137) (2-й справа), учитывающий теплообмен путем диффузии. Граничные условия для одновременных уравнений сжимаемых ламинарных течений .
Форма пограничного слоя химического реакционного газа выглядит следующим образом: Y = 0 i /-> oo P =РшP — > P1 T-> TTA = -H / = / шno. s = 0 ^ — > 0 Cf = Cllo (XI-143) тепловой поток в ламинарном пограничном слое идеальный диссоциационный газ при dp / dx = 0.Определим тепловой поток к пластине, который рационализируется диссоциацией gases. To упростите эту проблему, передача тепла Это реальная смесь газов, которые реагируют, но газы, которые полностью диссоциируют. Таким газом называют смесь, состоящую всего из 2-х следующих компонентов. Масса / la, а tm = 2 tl. In кроме того, в этом .
Газе происходит только реакция вида химической реакции приведенной выше системы уравнений пограничного слоя в смеси газов (Xl-130, XI-131, XI-132, XI-133, XI-137 и XI-143), как и для газов, которые полностью диссоциируют. Это связано с тем, что в идеале диссоциированный газ является самым простым Частный случай смеси химических газов. Для газов, которые идеально диссоциируют, вводится следующая запись: a= — концентрация атомов, P 1-a) — = — £m. — концентрация молекул. Уравнение энергии пограничного слоя (X1-136), a / i показывают 4 —(1-a) Am; Л«=о (XI-I44)(XI-145) (XI-146) D-энергия диссоциации 1 молекула в газе, который полностью диссоциирует. / э = б-’my⁷+ л «; Х1-1⁴⁷) о AJJ = 0.
Потому что энергия не расходуется на образование молекул газов, которые в идеале диссоциируют. Другие Химические реакции в особых случаях уравнение пограничного слоя в газах-в идеале, диссоциирующий воздух не изменяется или только воздух в них отличается вместо концентрации i-го компонента Ct концентрация здесь не показана, так как это, например, атом A. В идеале мы сравниваем уравнение энергии пограничного слоя. Замените диссоциированный газ (X1-144) уравнением энергии диссоциированного газа (X1-19) и замените dT в последней воде на dh.
Это сравнение показывает, что новые члены (X1-144)( Справа) связана с передачей энергии путем диффузии. Перейдем к определению теплового потока. Это значение ламинарного пограничного слоя не диссоциативное газ、 Закон Фурье (1-3) тепловой поток ламинарного пограничного слоя идеально диссоциирующего газа равен dT, r \ .., x да — ^ — +pD₁₂ (aₐ-FTM)-можно выразить в виде. (Си-148) Разность энтальпий 2 компонентов атома с учетом (X1-146) и(X1-147) / / молекул а И ЛМ можно записать следующим образом: L. — ym =Л5+ $(сРа-сри)^. 0» «(СРО-С » Г) ДТ^. (Си-149) (XI-150) соответственно (XI-148) будет (XI-151) и формат dT, p. 0 Да — — » 7-F P ^ ie ^ a — Г— — •концентрация атомов в основном объеме пограничного слоя oy.
Только температура, то есть a = a(T).Затем напишите yes da dT ^ du dT du комбинируя(XI-151)и (XI-152), последнее выражение — + M-m-» ХС = ро, РЛ.- §(X1-152) (XI-153) (XI-154) (XI-155) величина Xr называется коэффициентом теплопроводности по М и химической реакции. Сумма (X — | — Xg) называется очевидной Теплопроводность. Если мы введем сумму (X 4-Xg) вместо X в уравнение энергии (X1-144), мы получим член (2-й член справа), связанный с переносом энергии диффузией) Комплектующие.)Полученное таким образом уравнение энергии пограничного слоя в диссоциированном газе по форме не отличается от уравнения энергии пограничного слоя в несвязанном газе.
Ранее было установлено, что решение уравнения нереактивного газа (VII-48) несжимаемого (p = const) пограничного слоя может быть представлено в виде: St = — (Рг) 3 。 (XI-156) он эффективен против сжимаемого газа (гл. XI,§ 3). Исходя из (VI1-47), тепловой поток от ионизирующего газа к стенке равен −7 = Pi Pr (/ᵣ-hw)ₜ (XI-157) где г= ftj 4-r-энтальпия восстановления. / gh и hw-энтальпия на внешней кромке и температура стенки пограничного слоя. r = — URg-коэффициент восстановления. РГ = (XI-158) — число Прандтля в соответствии с составом и параметрами смешанного газа. Решение системы уравнений пограничного слоя в идеально диссоциирующем.
Газе может быть выражено в следующем виде: Аналогично(X1-156) эта система не отличается от системы уравнений недиссоциативных газов, поэтому если последнее X заменить суммой (X +М -, то решение граничного уравнения Идеально диссоциирующие слои газа могут быть представлены в виде St = — ^(PR₍ ₍ ₍ ₍), «(XI-159) и pr1.₉ = — T-77-число Прандтля, газ согласно полю подачи Смесь. Тепловой поток от идеально диссоциирующего газа на основе (VI1-47) и (XI-157) может быть выражен в виде −7 =-^-Р₁ (PRM)〜5-(/ᵣ -ff[ₗ)). (XI-I60) после преобразования .
Форма формулы (X1-160) [27] -?= — ^- R. 2/, Pr-2/3 (/,- Л») xrr₁ ₊ ₍ ₍ l_i) 14.( XI-161) LJ формулы сравнения (XI-157)и (X1-161), последняя имеет дополнительную Коэффициент (в скобках) отражает влияние диссоциации на теплообмен в продольном потоке вокруг пластины. Влияние диссоциации на теплообмен пограничного слоя является идеальным диссоциация газа при dr / dx-О анализируя уравнение теплового потока (X1-161) в пограничном слое идеальной диссоциации, можно судить о влиянии диссоциации на теплообмен. Газ.⁽⁽22⁾диффузного пограничного слоя найдено при анализе уравнения диффузии (XI-143). I-характерный размер тела; PeB — ^ l =Re₁PrB (XI-163) — диффузионное число пекла. Ре.
Число Рейнольдса. На основе V (VII-8)можно описать динамическое отношение толщины пограничного слоя 6 ′ —4 =. (XI-164) и на основе (V1I-34)-термическая толщина Пограничный слой D ’ — _ (XI-165) / Pii, где Pe -= — ^ 1-число пекле. Сравнивая (XI-166) (XI-162) и (XI-164), мы можем видеть соотношение диффузной 6C и динамической 6 толщины. Для пограничного слоя(XY67) отношение толщины термического D к динамическому 6 пограничному слою задается формулой (XI-44).Уравнения движения и энергии (VII-35) В безразмерной величине без условий=они будут идентичны, но относительное распределение скорости и температуры одинаково.
Вдоль потока Пластины при условии — ^ — = «Re ^или PRI v» — абсолютное распределение скорости, температуры и концентрации (Атом а и др.) аналогично, и относительное распределение этих Количество-это same. It иногда говорят, что в этих условиях есть 3 сходства, так как процессы передачи импульса, тепла и массы похожи друг на друга. Разнообразие В некоторых случаях диссоциация оказывает различное влияние на тепловой поток. Рассмотрим несколько характерных случаев. Если число Льюиса (XI-142)равно 1, то Pr = — ^ 1 XI — = — число Прандтль; х и РГД=-= ———рассеянный плантрил номер. pO] 2 в случае 0J2 Le = 1 или a =Dₗ₂ термин, заключенный в квадратные скобки, удаляется из выражения (x1-161).
Феномен диссоциации. a =£>ⱼ₂ имеет одинаковое относительное распределение температуры и концентрации по всему пограничному слою. Если нет реакции на стену в этих условиях Рекомбинация атомов в молекулы, теплопроводность и диффузия интенсивность теплопередачи массовым потоком одинакова. Здесь мы имеем в виду только концентрационную диффузию. Другими словами, диффузионный массовый поток не вызывает дополнительного теплообмена с величиной передаваемой теплопроводностью. Поверхность плиты В катализаторе происходит экзотермическая реакция рекомбинации молекул на атомы и приводит к дополнительному теплопередаче.
Эта дополнительная переноска Он описан в терминах (/g-Kw) b (XI-161).Давай поговорим об этом. На основе (XI-138) и (XI-145) разность энтальпий (г-hw) равна rц> > (La ^ m) 11+(LM) 1 4″ 4 ″ ^ — (La Лм) вопрос, aw4 _ (^м) «с ранее принятыми (Ла-Лм) 1» м «(Ла-Лм) Вт, следовательно lᵣ— гв»Л5 (а!!!) «- Aᵤ.) 4 — (ftM) ₗ — +(XI-168• * поверхность объекта, на котором протекает каталитическая реакция(стенка) Химическая смесь, которая вступает в контакт с поверхностью, называется катализатором [74].Первый член уравнения (X1-168) описывает влияние диссоциации на теплопередачу, как если бы Le .
Заметим, что если = I, Le # = 1, то диссоциированный воздух соответствует числу Льюиса в 1.4. когда when = al, то есть поле концентрации атомов и молекул в пограничном слое Он однороден и не вызывает концентрационной диффузии. в случае = ctw термин в квадратных скобках выпадает из (X1-161), а первый член выпадает из (XI-168). в обоих случаях эти термины являются Поэтому в этих условиях диссоциация практически не влияет на теплообмен. Уравнение (XI-161) не учитывает влияние степени диссоциации переносного Характеристики газовой смеси, например, количество прандлей, но этот эффект невелик, поэтому особых погрешностей не возникает.
Смотрите также:

