Тонкое крыло

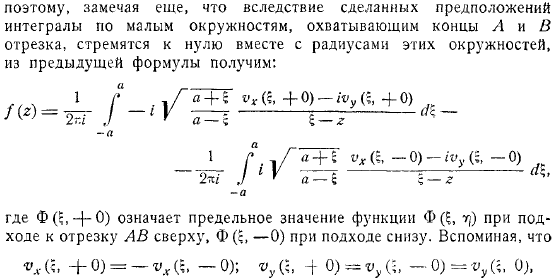
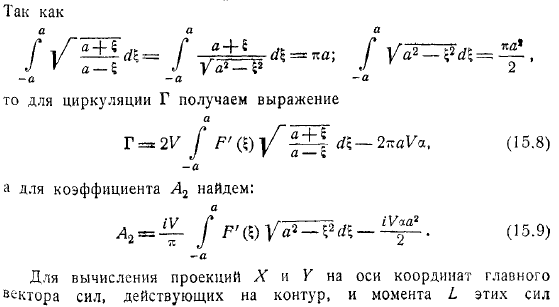
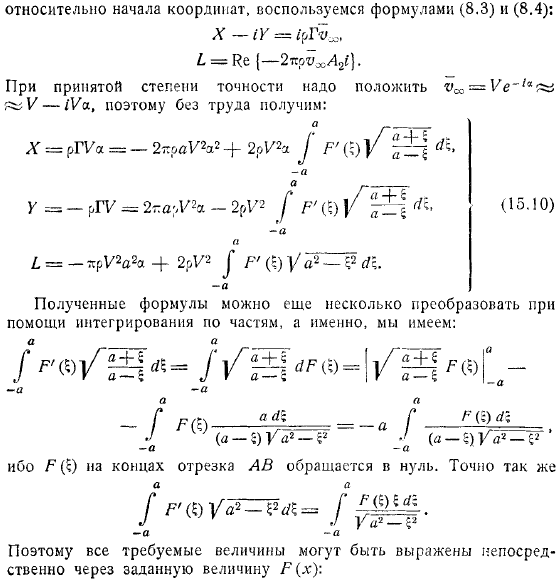
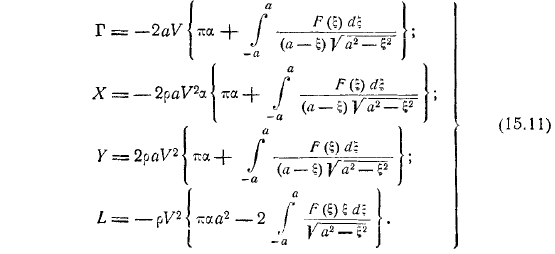
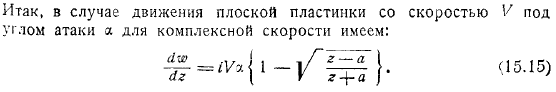
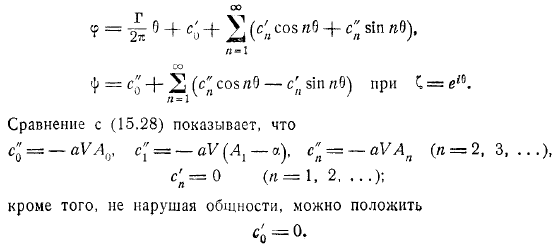
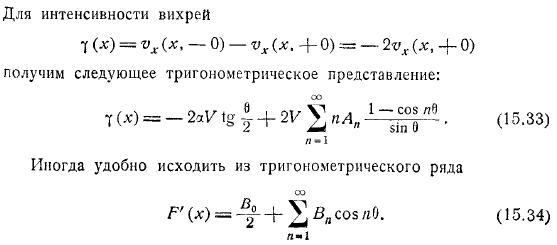
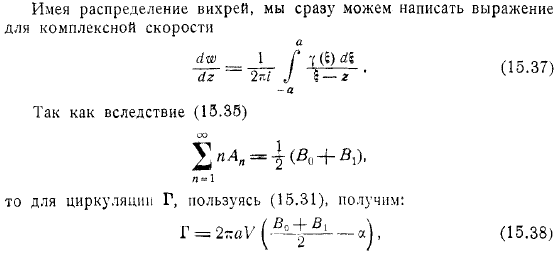
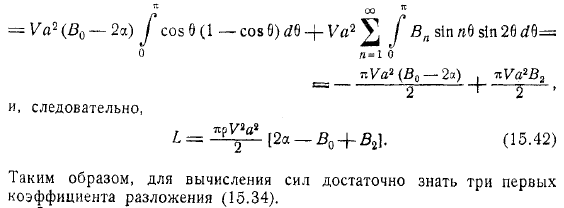
Тонкое крыло

Как мы уже видели, если мы знаем конформное преобразование контура окружности наружу, то задача обтекания контура любой формы будет решена до конца. Однако очень трудно найти гидромеханику явную форму этого конформного преобразования для любого профиля формы. В настоящее время существуют эффективные методы аппроксимации для решения задачи обтекания. Из них наиболее развитыми являются метод Симонова и Северского, который может быть использован для расчета обтекания любого профиля, но его изложение выходит за рамки данной публикации.

Другие приближенные методы решетки , связанные с определенным типом контура, например, подходят только для тонких профилей. Мы поговорим об этом подробнее. В общем виде мы покажем, как дать приближенное решение задачи обтекания любого тонкого профиля. Мы. Замените последнюю кривой, проходящей точно посередине верхней и нижней части контура. Предполагается, что уравнение этой линии присутствует. Для наглядности предположим, что оба конца дуги находятся в точках на осях с координатами на рисунке. Поэтому, предположим, что кривизна контура очень мала.

Сама схема с практически ничем не отличается от отрезка прямой линии. Поэтому функция, определяемая отрезком на оси, имеет непрерывную производную порядка, которая считается бесконечной величиной, исчезающей в конце этого отрезка. Рассмотрим задачу обтекания контура. От обусловлен поступательным потоком со скоростью, наклоненной к оси под углом атаки под бесконечным углом, что также считается малой величиной. Или, точно так же, задача о поступательном движении контура со скоростью в направлении, образующем отрицательную ось и угол.

В этом последнем случае мы показываем комплексный потенциал результирующего абсолютного движения жидкости для комплексного потенциала, определяющего обтекание контура. Поскольку схема является линией потока задачи о потоке, она имеет постоянное значение и может считаться нулевой без ущерба для общности, поэтому мы получаем. Меньший порядок и предположения о a позволяют отбросить меньшее или равное и заменить. В результате получаем граничное условие. Из-за сложных возможностей.

Для комплексной скорости, граничное условие для. Комплексная скорость является уникальной особенностью, поэтому ее удобнее рассматривать. Таким образом, перенос граничных условий из контура в проекцию на ось оси является слабой кривизной контура, что упрощает задачу быть мощным. Предположим, что острые кромки начального контура соответствуют задней кромке контура и, соответственно, необходима конечность скорости в точке. На переднем конце скорость обычно бесконечно велика, и произведение вблизи точки, где расстояние точки относительно, остается ограниченным.

Заставлять. Компонента скорости непрерывная на отрезке. Компонент является разрывным, но разрыв тангенциальной составляющей скорости можно рассматривать как наличие вихря. Можно предположить, что рассматриваемый поток нисходит из системы вихрей, которые непрерывно распределены на отрезке оси. Затем возьмите симметричные точки и к основанию относительно оси. Очевидно, что вихри на оси дают скорость этим точкам с одинаковыми компонентами вдоль оси и диаметрально противоположными компонентами вдоль оси.

То же самое верно и для всей системы вихрей, распределенных по всему сегменту препарата. Следовательно, существует уравнительная. В частности, в сегменте касательная компонента скорости при приближении сверху и снизу имеет одинаковый модуль, но знак противоположен. Теперь рассмотрим функции также получим положительное значение корня в. Эта функция регулярна во всей плоскости разреза вдоль отрезка оси и исчезает при. Охватывает сегмент и обозначается контурной линией, идущей по часовой стрелке.

Функция, проходящая через внешнюю точку контура, имеет единственную особенность вне контура, за вычетом остатка функции на дальнем конце. Исполняемых сегмента. Поэтому понятно, что с верхней стороны этого сегмента надо брать нижний сегмент. Также отметим, что при допущениях интеграл малой окружности по ребрам отрезков стремится к нулю вместе с радиусами этих окружностей, выведенными из предыдущей формулы, что означает предельную функцию при приближении к отрезку снизу вверх.

Леонид Иванович Седов — советский, российский физик, механик и математик, академик АН СССР. Людмила Фирмаль

Не забудьте получить формулу. Замените значение здесь. Это потому, что окончательное решение проблемы находится в форме. Мы находим разложение этой функции вблизи точки бесконечности, так как она легко получается по аналогии с то. После этого для циркулирующей гаммы получаем формулу. Для коэффициента находим для вычисления моментов этих сил на проекциях по координатным осям главного вектора сил, действующих на контур, и на начало координат используем формулу: и так далее. С принятой степенью точности, вы должны положить в. Поэтому, вы можете получить его легко.

Полученные формулы могут быть дополнительно преобразованы путем интегрирования. Другими словами, исчезает в конце сегмента. Таким же образом, а, следовательно, все необходимые величины могут быть представлены непосредственно определенной величиной. И в качестве примера рассмотрим случай с квартирой. В этом случае достаточно выразить его непосредственно и получить формулу циркуляции и силы. Задача обтекания пластины точно решена, и ясно, что полученные результаты теперь совпадают с результатами, полученными из точной формулы малого угла атаки.

• Комплексная скорость в рассматриваемом случае задается формулой: формула. Интегральное состояние на правой стороне легко поддается вычислению. Дело в том, что функция регулярна по всей плоскости разреза вдоль отрезка и становится пулей на бесконечности. Таким образом, формула — это опять же применимо. Если вы нарисуете контур в выполняемых сегментах, вы найдете в верхней части этого сегмента. А внизу есть из уравнения. Получает, следовательно, для пластины, которая движется со скоростью угла против комплексной скорости.

У нас есть широкий выбор по отличным ценам, чтобы помочь вам получить творческий подход. Найти предельное значение комплексной скорости при приближении к точке отрезка от. Когда вы приблизитесь к дну, это будет. Интенсивность вихрей распределена в сегменте. Скорость, которая может быть использована для замены контура для получения рассматриваемого потока, определяется касательной составляющей скорости, а следовательно, и разрывом. Общая интенсивность движение плоского контура всех этих вихрей четко определяет размер циркуляции.

Сила вихря исчезает на заднем конце крыла, где скорость остается конечной, и сила вихря растет бесконечно к переднему концу крыла, и это связано с наличием бесконечной скорости около переднего конца крыла и наличием силы всасывания. В качестве примера рассмотрим параболический лук. Если вы будете исходить со сцены, то без труда получите и др. Циклическая сила и подъем исчезнут, поэтому проходящая линия будет критической осью. Верхний и задний концы лука. Генерал. В этом случае используйте. Полученную формулу.

Получите также о силе вихря без каких-либо трудностей. Вы найдете. Когда вы переходите от переменной к переменной и вводите, предыдущее выражение принимает форму. Способ решения описанной здесь проблемы. Принадлежит Седову. Вот еще один способ решить проблему тонкокрылых. Конформное преобразование внешнего отрезка во внешний отрезок окружности единичного радиуса плоскости. В частности, представление для точек отрезка при размещении на диске, получается. Сложные возможности удобнее найти на плоскости.

О ее мнимых частях имеются. В этом разделе мы введем обозначения. После этого предыдущее условие можно описать в виде. Используйте для расширения четной функции тригонометрических функций. Следующий. Однако комплексный потенциал плоскости должен быть разложен на ряд форм, которые заменяют этот ряд, чтобы разделить реальное и мнимое. Это отличный способ не отставать от своих друзей и семьи. Кроме того, не теряя общности, его можно расположить следующим образом: в результате мы достигаем следующего представления потенциала в окружности. Замените выражением здесь.

Получаем потенциальное значение cp отрезка. Теперь вы найдете тангенциальную составляющую скорости выше и ниже профиля. На верхней стороне сегмента угол изменяется от. Держите скорость конечной на правом конце соответствующего лука, вам нужно взять. В конце концов это будет. В нижней части профиля, скорость будет меняться знак компании. Для интенсивности вихря получим следующее треугольное выражение. Мне иногда удобно начинать с тригонометрической функции. В результате. И так далее. Определить да, потому что у нас есть. Существует связь между. Присвойте это значение, после простого преобразования.

Вы найдете: до конца. Например, для параболической арки. И скоро вы получите формулу. Если есть распределение вихрей, то можно сразу написать формулу комплексной скорости. затем используя циркулирующей гаммы, после чего формула силы выписывается Получаем момент относительно координаты начала действия силы, действующей на профиль, разворачиваем его. Вблизи точки бесконечности и по формуле. Поэтому для расчета силы достаточно знать первые коэффициента разложения.

Герой Социалистического Труда, лауреат Сталинской премии второй степени. Людмила Фирмаль