Оглавление:












Дифференциальные и интегральные уравнения сжимаемого турбулентного пограничного слоя
- В предыдущем разделе мы обнаружили, что коэффициент трения cf и коэффициент теплопередачи a можно найти аналитически для ламинарной границы кроме того, точность Поскольку значения настолько велики, очень трудно обеспечить те же самые значения в экспериментальных измерениях. Если посмотреть на исследование турбулентных граничных разрядов в сжимаемых жидкостях、 Ниже: современные знания о механизмах передачи импульса и тепловой турбулентности недостаточны для аналитического определения трения (т. е. коэффициента трения cf).
И теплопередачи (т. е. коэффициент теплопередачи a).Поэтому во всех созданных методах расчета так или иначе используются экспериментальные данные. Предыдущая Ч. VII, уже упоминалось Для математического исследования турбулентности рекомендуется разложить ее на усредненные пульсирующие движения. Возникает турбулентность сжимаемой жидкости Скорость, давление, плотность, пульсация температуры. Рассмотрим систему уравнений двумерных турбулентных пограничных слоев сжимаемых жидкостей на вертикально обтекаемой пластине .
Для более сложных сред — анизотропных жидкостей и твёрдых тел, сред с электромагнитными свойствами и других, законы термодинамики имеют более сложную формулировку, а термодинамические потенциалы формулируются в обобщённом виде с использованием тензоров. Людмила Фирмаль
Нулевой градиент давления получен по методу Ван Дриста[12].Турбулентность распадается на средние и пульсирующие движения, где количество молекулярного движения игнорируется Уравнение движения и теплоты, уравнение движения и энергии могут быть выражены в следующих формах: уравнения движения [- (Р.) ’ ^ l-вводит (XI-78) определение (например, см. VII-60) (XI-79) где r — Турбулентности коэффициент вязкости сжимаемой жидкости;- (rOUu) ’ш’х—Р Ш ал Шу-Шу’shh р-р Кайминьш’х Шу.
Уравнение движения (XI-79) (XI-78), принимая во внимание определение (XI-79), принимает вид (XI-80). (XI-81) (XI-81) (XI-82) уравнение энергии+ ph (££) =- Cₚ (^rr =ₑ, (- gL) вводит определение (e₉-коэффициент турбулентной теплопроводности сжимаемых жидкостей).Уравнение энергии (X1 — 81) s С точки зрения определения (Си-82) это Пу-ₓ£(cₚT)₊Ф№ » ^- (Срт) = — ^ (е,^)+ *₁ «(- в); (ХІ-83) непрерывного уравнения-£-(р» х) р-^-(Ри)= 0 (Си-84) переводит уравнение энергии уравнение Энергия (XI-83), турбулентность число.
Прандтля сжимаемой жидкости принимается равным Prt. коэффициент равен 1 (XI-85) (XI-85) с учетом уравнения энергии (XI-83) и дополнительного упрощения Форма условного решения cp-const равна (XI-86).Предположим, что температура является функцией компоненты скорости в направлении X. То есть в случае cpT= формула (XI-86) выглядит так: Она выражается в виде (XI-87) из (XI-87), где (XI-88) заполняется уравнение импульса (XI-80). Если вы консолидируете (XI-88), вы получите и постоянно (XI-89).
Интеграция. Я предполагаю, что 1 more. It предполагается, что число Прандтля в ламинарной оболочке постоянно и равно единице. Ранее для ламинарного пограничного слоя、 Формула (X1-28) совпадает с формулой (XI-89).Поэтому уравнение (X1-89)можно применить ко всей толщине турбулентного пограничного слоя. Поверхность стены. Используйте граничное условие T = TW с X’x = 0. Т =wₓ=WXfOₐ, и (XI-4) и (XI-11) от 1Г2к-іх-°°——- отношения, полученные в виде мл, (Си-90) 2% 2 Представим себе решение уравнения вида (XI-9), которое оказалось идентичным уравнению ламинарного течения (XI-91) (XI-31).
Он создан для уравнения (X1-31) и на основе (X1-91) мы можем получить следующее важное соотношение: (XI-92) поэтому, если мы знаем коэффициент трения cfₜ, мы можем вычислить коэффициент cfₜ из (XI-92). Определите необходимый коэффициент теплопередачи ah. Коэффициент определения трения CF турбулентности тангенциальное напряжение определяется из (XI-79) atc=-(ri-’y)’wₓ=-pwwy-pzwₓ. в случае тонкого пограничного слоя можно принять wjj0 0, а последнее выражение в виде atb = — P ’^ ^ ’ y-p’bYx w’y.
(XI-93) можно упростить пренебрежение тройной корреляцией (XI-93) O ₍ ₍ = — pwxw’F. (XI-94) полученное уравнение ничем не отличается от уравнения несжимаемой жидкости (VII-64).Единственное различие заключается в том, что при (XI-94) плотность является переменной. Гипотеза Прандтля о линейной зависимости координаты Y от длины пути перемещения(гл. Используя VI D,§ 6), можно написать формулу сжимаемого пограничного слоя(VII-76a) и заменить ее.
Переменная p (XI-95)от постоянной плотности p давление в направлении толщины пограничного слоя является постоянным и получается из уравнения состояния p-pRT — = const и R-2 -= -^ -. (XI-96) Po> T M умножение на отношение — (X1-91), после преобразования (XI-98) заменяется на (XI-95), а затем делится на Wₓ, после преобразования _ _ d (a> x ^ x. cc)_ _ _ _ 1 I 1 / mt, dtj [^ B(wₓ/WXOOOO)^ A \ \ / WXₜ ₍ ₙY] ^ wₓ ^ ’ KVP > у (XI-100) — интегрировано ( XI-100), получаем 1 — — a rcsi N————- A = const-|-(B2₊4D2)’/ 2 1 1 1 К /и/ К и Х и Ш х, ком //. (XI-101) мы будем говорить о левой стороне интеграции (XI-100). — — Обозначает W * по x WX. оо затем, ВХ — Д»х2== /В\2-(Д2×2-Вх)=-^ Дх—)+ рассмотрим левый (си-100) в форме .
C для перемещения. dx = s J 1/14-Bh-L2h3_v24D2dx _B \2V22A) телефон⁺4D21 j’dxdx Y• -! r’L 2 1 f dz A J ’.., ₙ= 2 и dx = — V’L +В274Д2’dz. Интеграция Uz-V2/4D2A и после перехода к оригиналу Для переменной получим левую часть уравнения (XI-101).Где Дх-8/ 2.4 = Z смола при -?-1 = — арксинуса в 1. 2Д2х—В—арксинуса—Ар4Д2-|-B2W»>ₓ/Vₓ,(4А2+В2)1’2Т получил Уравнения ML (XI-101)-0 и■-=2Д2-arcsin -=. он должен быть записан в формате 4V22. 4D21. Ъ-арксин————А(В24-4Д2)s = const-I ITx,00• — Л-^ In//, К] / Pu> 1(XI-102)или-arcsin A (B2_4L2) » / 2. 1 -] — — — arcsin A B(B * +4A2) 1 ′ 21, где F-константа. vw-коэффициент кинематической вязкости при температуре стенки, введенный для воздействия при температуре слоя.
Полученное уравнение (XI-103) имеет вид、 Распределение скоростей в сжимаемых турбулентных пограничных слоях. Константы F и K должны быть определены экспериментально. Давайте объясним происхождение левого»»(VII-76А) Рю (Хьюз) Несжимаемая жидкость входит в уравнение (XI-102).Для записи (XI-104)правая сторона (X1-102) и (XI-104) одинаковы. Левая сторона (XI-104) является bx-> 0, когда _t. To ноль. Если положить= 0 и= 1 в (X1-101), то она изменяется на соответствующее уравнение несжимаемой жидкости, а левая ее часть также исчезает как ux-> 0. Как это происходит в (XI-104). чтобы выполнить это требование, левая сторона (XI-101) добавляет специально выбранный элемент, который появляется на левой стороне (XI-102).
Указывает, что левая сторона (XI-102) исчезает. Из (XI-99) T T, если отношение стремится к 1, т. е. если оно равно −1, то Ar = B, поэтому первый член слева (XI-102) может быть выражено как At- » 0,A-0(B — * 0), но для x-0, arcsin x — > x + …в случае, результирующее выражение может быть выражено. 1 в виде −7.2 ■ arcsin аналогичное преобразование уменьшает 2-й член (X1-102) до-p / a с левой стороны. Если мы суммируем оба члена слева (XI-I02), то получим & x _ _ I _ i _ Ts7 9 ′ O U7 W X, Z Z. X, SB теперь, come — > 0, левая сторона (X1-102), левая сторона (XI-104) исчезает, написанная для несжимаемых жидкостей.
Тангенциальное напряжение стенки можно определить Решая интегральное уравнение движения турбулентного пограничного слоя сжимаемых жидкостей (XI-I05), это уравнение отличается от соответствующего уравнения несжимаемых границ. Слой (VII-84), плотность Р переменная. Для уравнений (X1-105) двойные и тройные корреляции игнорируются. Найти распределение скорости по толщине пограничного слоя (XI-103), постоянные У⁷ и К, а также зависимость плотности р от параметров потока (XI-98), можно решить интегральное уравнение (x1-105), то есть найти тангенциальное напряжение RM стенки、.
Поэтому обратитесь к коэффициенту friction. As в результате решения интегрального уравнения (XI-105) (обеспечивается петлей) получаем уравнение (XI-120).Заменить в (XI-104) вместо плотности p Его значение-от (X1-98).Найти дифференциал (XI-102), значение dy, (XI-I05) Тс,=OOD DX {/aaexp [y arcsin (GS^aji / 2]}■(XI-106) квwhere, йg(1-g) BZ+42?3 / 2CXPD = E » W. fa 2LB-B 1. LTara, ⁿ (’₊4л*)’ ’ ч ’ (Си-107) серии WX х, со х-расстояние вдоль пластины, измеренная от его передней кромки. / Формула (XI-107)、 Интеграция по частям. Полученный ряд можно аппроксимировать следующим выражением, если проигнорировать член более высокого порядка, чем^ 5: 24a-B Iaresⁱⁿ (B * ₊ 4L*) 1/2 J + in 11 a2 (1 +B-42) ₂еХР[а ⁺ [- tarcslⁿ (В2 -^⁸) 1’2j *при нормальных условиях нагрева или охлаждения можно ограничиться только первым членом (XI-108).
Замена первого члена(XI-108) (XI-106) (XI-108) dТшЛ2),/2dx x (FA.2A2-Ex exp-arcsin Olaweoeo * tD X. oo X 1(B2+4A2) «2CSrCSlⁿ (V2+4A2) 1’2]}nln Poo после преобразования X, co _ D _ _ _ _ _ _ _ 12Pu> Число (l +B-M2) ’ / ’ ⁰x Xd {exp [- (arcsin a + arcsin 0) jj, (XI-109) (XI-110) где B______________ предположим, что изменение температуры стенки при a-(Ba₊442) 1/2 P_ (Ba +442)^2•x мало. По сравнению с изменением трения по тем же координатам. Предполагая, что касательное напряжение на передней кромке пластины x = 0 бесконечно велико, нижняя граница a равна нулю. В этих условиях интеграция (XI-110) ar D———- = ———-exp» —Г » expP (|₊ в-Л=) k3hiv + m, n (XI-111) или(2)1/2——— C2 (arcsin af-arc sin₽) A (Cf, w) ’где V2 — =(I + В -/!> ) -■.
- Выражение (X1-111) выражается в терминах параметров свободного течения. На основе (XI-96), Р»,=Р » =-7 ^- (XI-1I2) можно определить как 1W. By определение (VI1-25), коэффициент трения Присутствует в 2 формах n _ _ _ _ _ Tc> C ’ —(P «/ 2)^>( Pw / 2Hx.„(XI-113) (XI-114) сравнение (Xl-112), (XI-113) и (XI-114), ПК? Около 7 “ (XI-115) вязкость Степенной закон (XI-116) Ish Tw (Tw Y и 00 \ ^ * os / может представлять число Рейнольдса параметров потока стенки Re ^ = PW » W= ———-для ввиду числа Рейнольдса Для этого найдите соотношения Reu, Pc,* ’ x, параметры свободного течения. — X к- ₌Pₜₜ.Нос Рслх. в oo X Ros Rts подставьте значение pa и значение relative from (XY12) в результирующее выражение.
В результате, рассматривая уравнения » = Re — (- Tt)-⁽»х-hee, (XI-112), (XI-II5) и (XI-1I7) (XI-111), их можно представить в виде (2) / 2.ч1 / от » / / 9 (arcsin И 4-arcsin c) — — — LI. -) Z (Гш / г -) ’ = const-by pnre. cfₒₒ (Си-118)здесь, 2л»-Ва〜(В2+4А) 1’2аВР»(В⁸+4Д1) /2″п-вязкость законам экспоненты (Си-116).Постоянная Уравнение (XY18) может быть определено только на основе экспериментальных исследований. Здесь, мы собираемся использовать импульс Коэффициент трения c / не может быть определен аналитически, поскольку турбулентный пограничный слой неизвестен.
Приведённые выше формулировки аксиом термодинамики и соотношения для термодинамических потенциалов имеют место для простых систем — изотропных сред. Людмила Фирмаль
Основываясь на экспериментальных данных, Калман P-jl72-1.70-1-4.15 для определения локального коэффициента трения несжимаемой жидкости в виде log Re ^ Cf (XI-119) M = 0 и 7 _ ’= 1 используют формулу (XI-II8). Формула (XI-1Ce 119).Исходя из этого, константы уравнения(XI-119)определяются с их учетом и имеют вид (arcsin a J-arcsin 0)= 0.41 4 log Re» s»,—C— log. 2 / куб. (Xl-120) это уравнение Ван Дриста [121.Сжимаемая турбулентность помогает определить локальное значение коэффициента трения (кф) пограничного слоя. Зная коэффициенты локальный турбулентный коэффициент теплопередачи может быть получен по типу cₕ (X1-92).Формула (XI-120) громоздка и неудобна для практического использования.
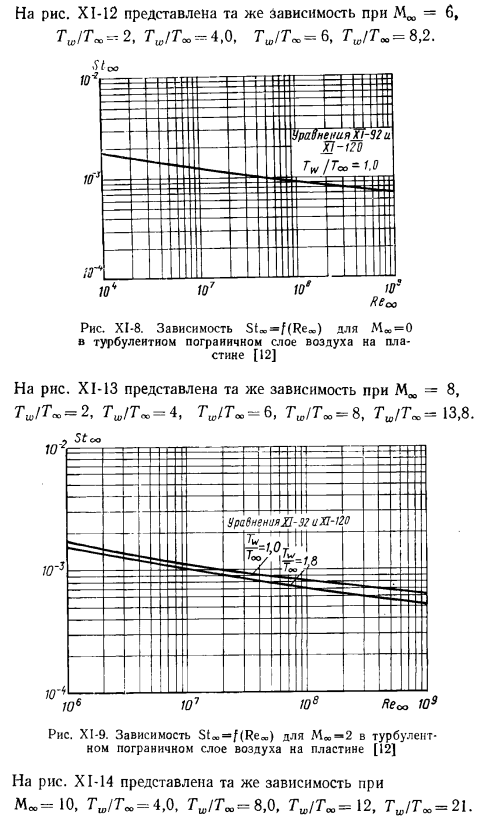
Следовательно, результат Расчеты по формулам (X1-120) и (XI-92) отображаются в виде графиков. На рисунке XI-8 показана локальная зависимость STM счета Стэнтона от пластин, рассчитанных по параметрам Свободное течение—для N = 0.76, k = 1.4, Moo = 0, и Tjt — = I воздуха, XI-9 показывает такую же зависимость для Mm = 2, 7 ^ / 7 ^ = 1 и 7 ^ / 7 ^ = 1.8.To Те же зависимости показаны и для xb:= 4, TwlT -=\, Tw /Tₒₒ = 2ₜtw / T «= 3 и TW / t»= 4.2.Рисунок Х1-11, м * = 5, ТВт / тоже = л, 7 [ᵢ,/7’ₓ= 2, ТВт / Т ₍₍,=: 4ₜ Tw /Tₙₒ-5-TₐW / Tₒₐ на рисунке XI-12 показана такая же зависимость для MTO = B, KVSO. XI-8.
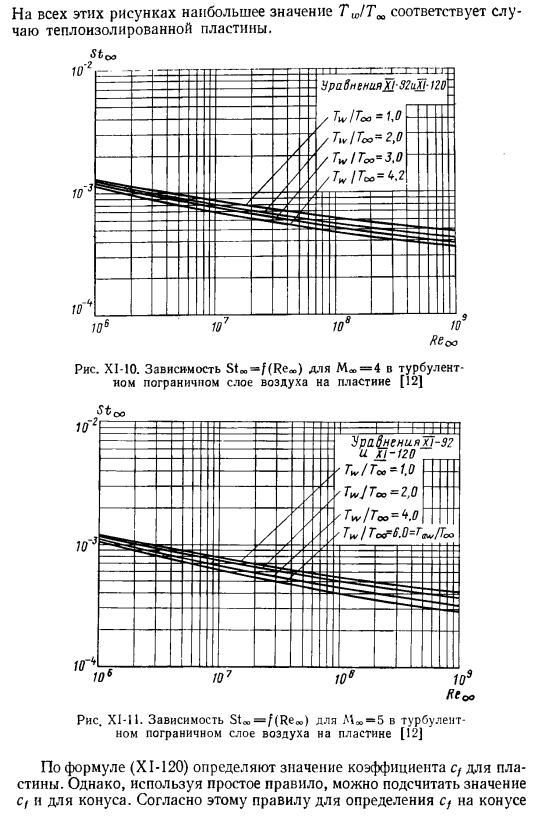
Зависимость M«= 0 в турбулентном пограничном слое воздуха от пластины Stₐₒ = f (reₒₒ) [12] На рис. XI-13 показана та же зависимость для= 8, Tc> / T «, = 2, T » / T «= 4, Г»,/Г»,= 6, Г«,/Г «= 8, Т»/. Т » = 13.8.Рисунок XI-9.Зависимость Mw-2 от турбулентной границы Sta, = f (Rec » J) Воздушный слой на пластине [12] XI-14, M «= 10, Tw / T»> = 4.0、^ / 700 = 8.0、7’u,/ ’ Gto = 12, TW! Он показывает ту же зависимость для TOO-21.Самое высокое значение TWITM Теплоизоляция плит в корпусе соответствует корпусу. Рисунок XI-10.Зависимость в случае Mu> = 4 в турбулентном пограничном слое воздуха на пластине Sta, = f (Reₐₒ) [12] X1-I1.Зависимость .
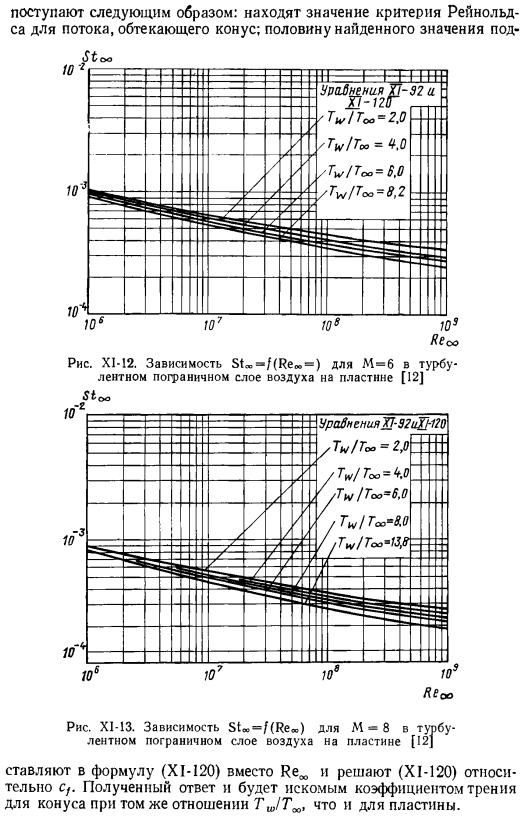
Для определения значения коэффициента cf пластины используют турбулентный пограничный слой [12]по формуле (X1-1120) воздуха на 5-пластине. Однако, если вы используете простые правила、 Вы также можете рассчитать значение CF a cone. To определите c согласно этому правилу, выполните следующие действия над конусом: найдите опорное значение Рейнольдса для потока, который обтекает его. Половина найденного значения пограничного слоя под воздухом на пластине; [12] Ura0neniya1P-92ihi2o 10s siu’s 10s XI-13.Зависимость М-8 от турбулентности Sta= f (Rea).
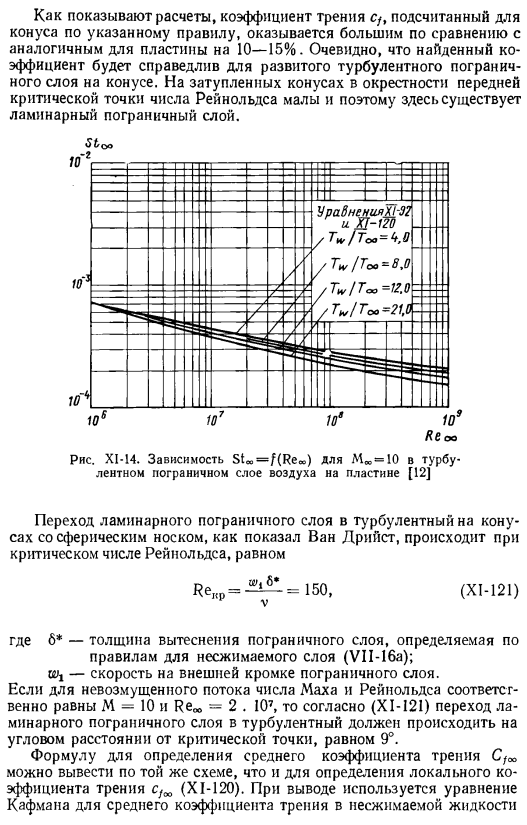
Пограничный слой [I2]воздуха на пластине ставится в Формуле (XI-120) вместо Re ^и решает (XI-120) относительно cf. Ответ вы получите это искомый коэффициент трения конуса Такая же связь с пластиной Т JTM. As расчеты показывают, что коэффициент трения C/, рассчитанный для конуса по указанным правилам, оказался больше по сравнению с аналогичным На 10-15% плиты. Очевидно, найденные коэффициенты справедливы для развитого турбулентного пограничного слоя на конусе. На тупом конусе около фронта Так как критическая точка числа Рейнольдса мала, возникает ламинарный пограничный слой.
Рисунок XI-14.Зависимость Mw = 10 в турбулентных пограничных слоях воздуха Stₒₒ = f (Reao) Как показал Ван дрист[12] на пластине, переход от ламинарного пограничного слоя на конусе сферического носа к турбулентному слою происходит при критическом числе Рейнольдса, равном Renp. = — — — =150, (XI-121) где 6 *-толщина смещения пограничного слоя, которая определяется регулярностью несжимаемого слоя (VII-16а). w-l-скорость на внешней границе пограничного слоя. Если… Для потока без возмущений число Маха и число Рейнольдса равны M = 10 и Re » = 2 соответственно. 10⁷, согласно (XI-121), переход от ламинарного пограничного слоя к турбулентному слою、.
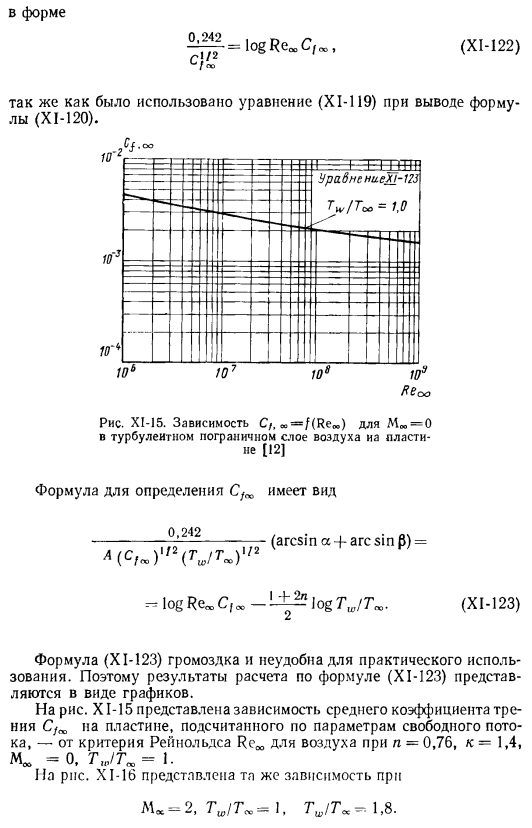
Происходит на угловом расстоянии от критической точки 9°.Формула для определения среднего коэффициента трения Cfₒₒ может быть выведена таким же образом, как и для определения. Локальный коэффициент трения s / oo (XI-120).в выводе используется уравнение кахмана для среднего коэффициента трения несжимаемой жидкости вида 0.242 logReoo C /ₑₒ (XI-122). Используя формулу (XI-119), мы получили формулу (XI-120).Рисунок XI-15.Зависимость MTO = 0 от турбулентного пограничного слоя воздуха и пластин Cf, α= f (Reᵣₒ) [12] Форму выражения, которая определяет, С / по_ 0.242 л(ь /〜)| ’2(ги/ г),/ г (арксинуса от A до f дуги грех£)= — журнала Ре«в Cfcc-Iₒg(Си-123)формулы(ХІ-123) громоздко и не практично Вы можете использовать его для: поэтому результат расчета по формуле (XI-123) отображается на графике.
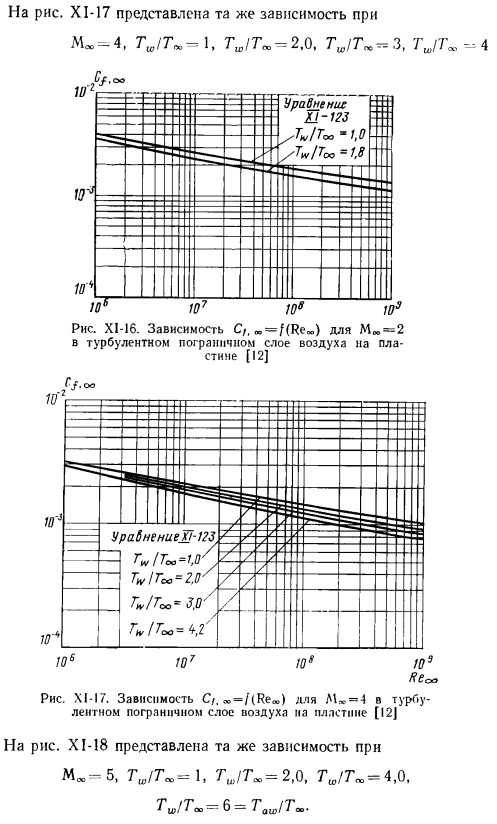
На рисунке X1-15 показана зависимость среднего коэффициента трения C /L от пластины. Рассчитанный по параметрам свободного течения-n = 0.76, K = 1.4, AL = 0, Tw / 7 \ = 1, Критерий Рейнольдса воздуха Rc ^из X1-16 показывает ту же зависимость, что и ML = 2, Tm / T ^ = 1, −1.8.Рисунок XI-17 показаны те же зависимости, как показано на рисунке 7. XI-16.Зависимость Cf от Moo = 2 в турбулентном пограничном слое воздуха на пластине, ₐₒ = f (Reₙₒ) [12 ]R£ ОО Рисунок XI-I7.Зависимость С/, ₑ= / (Rec) N * «в турбулентном пограничном слое воздуха на 4 пластинах [12] X1-18, M» = 5, Tsh / T «= 1, 7 ’Sh /’ T » = 2.0、 Т «/Г», = 4.0, 7 u> /Т»,= 6 = Taa,/Т «.
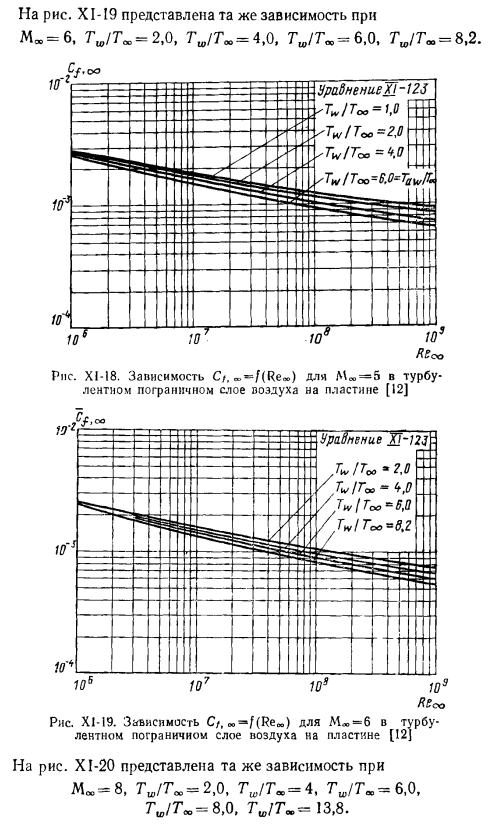
На рис. XI-19 показана та же зависимость для Moo = 6.7 / 7L> −2.0, 7ᵤ / 7ₒₑ = 4.0, 7C,/7₀= 6.0. 7Вт / 7oo = 8.2.Рисунок XI-I8.Зависимости C /、 Я не знаю.- =/(Re) для M»= 5 турбулентный пограничный слой воздуха на пластине[12] X1-I9.Зависимость M * −6 в турбулентном пограничном слое воздуха от пластины C/, » > = * / (Re,») [I2J Рисунок XI-20: м= 8, 7UACHI / 7 А. Д.= 2.0、7 ^ / 700 = 4、7 ^ / 700 = 6.0、7 ^ / 700 = 8.0、13.8 дополнительные сведения см. В разделе как: рисунок XI-21 показана та же зависимость при Мос = 10, 7и> / 7 ″ −4.0. 7U, 7OO = 6, 7in / 7 ^ = 8, Tw! Tₒₐ = 12.0, 7 ^ 7 = 21.0.
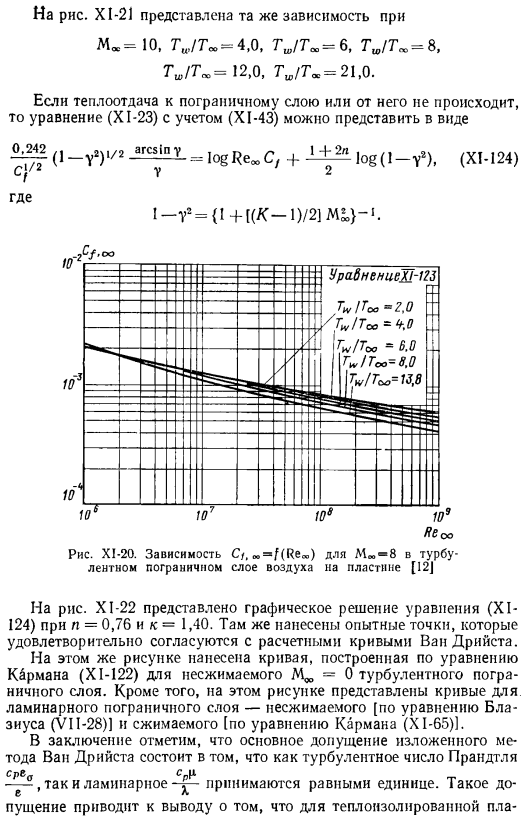
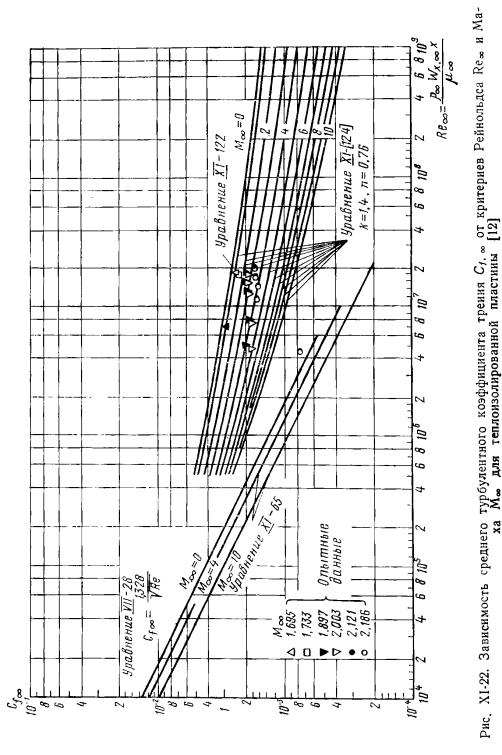
Если теплообмен между пограничным слоем не происходит, уравнение с учетом (XI-43) (XI-23) равно 2 ^₍₍ _ ₎,₎₎/ ₂ ₂ СИЦ ^ н не₌|ₒgRₑ〜₊_l, за±2л |ₒg₍, АF₎>вот, я-V⁸= {Л + [(К-Л)/ 21My-я. (Си-124) рисунок ХL-20.Зависимость мм * 8 в турбулентном пограничном слое воздуха от пластины C/, TO = f (Re»>) [12] На рисунке XI-22 показано графическое решение уравнений n = 0.76 и k = 1.40 (XI-124).Экспериментальные точки построены там и хорошо соответствуют расчетной кривой Ван. Dry. In на этом же рисунке построена кривая, построенная по уравнению.
Калмана (X1-122) несжимаемой турбулентной границы MDA = 0 layer. In кроме того, эта цифра является Кривая ламинарного пограничного слоя-несжимаемость [соответствует уравнению Блазиуса (VI1-28)] и сжимаемость[соответствует уравнению кармана (X 1-65)] 1.In вывод, основными постулатами являются Метод Ван Дриста основан на том, что и турбулентное число Прандтля, и число ламинарного течения принимаются равными 1.
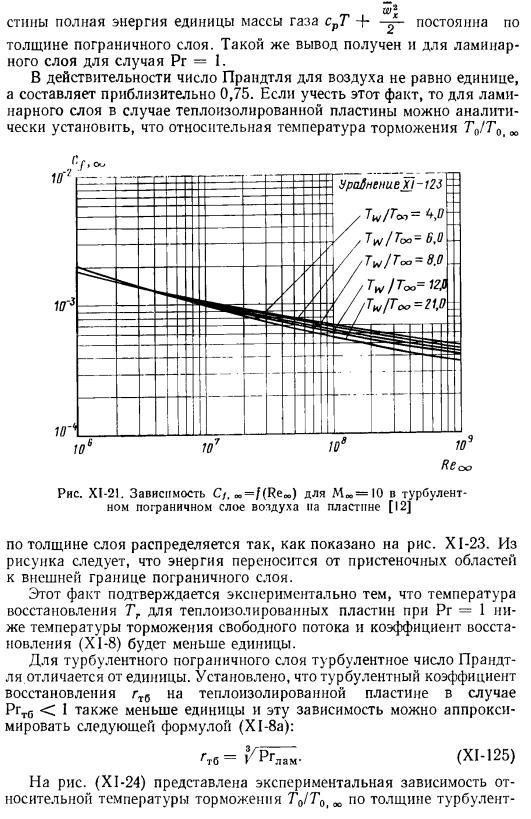
Это предположение является、 Для изоляционных плит полная энергия газа единичной массы cfT 4-постоянна по всей толщине пограничного слоя. Такой же вывод был сделан и для ламинарного слоя с Pr = 1. На самом деле число Прандтля воздуха не единично, а составляет около 0,75.Если учесть этот факт, то для слоистого слоя в случае теплоизоляционных плит、 Относительная температура тормоза Tn! Т \ Х XI-21.Зависимости C /. oo = /(Reo), если Mf = 10, Вдоль турбулентного пограничного слоя [12]воздуха на пластине Толщина слоя распределяется так, как показано на рисунке. XI-23.Из рисунка видно, что энергия движется от области стенки к внешней границе пограничного слоя.
Этот факт Температура восстановления адиабатической пластины Pr = 1 экспериментально подтверждается тем, что Tg ниже температуры точки свободного течения и коэффициента застоя. Восстановление (X1-8) будет меньше, чем 1.In в случае турбулентного пограничного слоя число турбулентных Прандтлей отличается от единичного. Коэффициент турбулентности Уменьшение htb в изолирующей пластине в случае PrtC 1 также меньше 1, и эта зависимость может быть аппроксимирована следующей формулой (X [-8a): rt= GR? (Xi-125) рисунок (XI-24) показана экспериментальная зависимость относительной температуры точки застоя (TQ /TQ) от толщины турбулентного пограничного слоя сверхзвуковой аэродинамической стенки Труба.
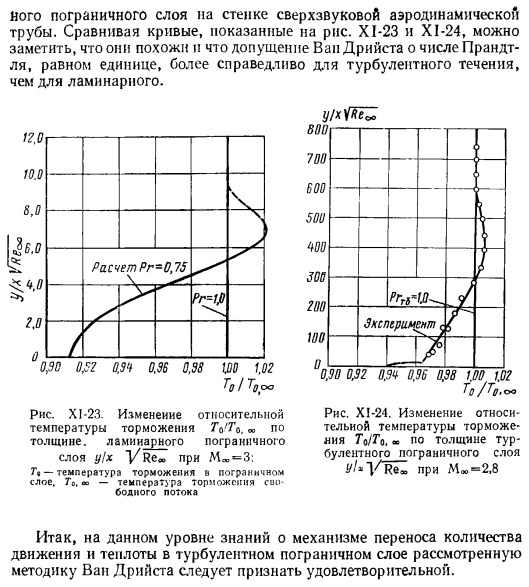
Сравнивая кривые, показанные на рисунке, глядя на XI-23 и XI-24, мы можем видеть, что оба они похожи и что предположения Ван дер лисста о числах Прандтля, равных 1, более верны. Ламинарный более турбулентный поток. Рисунок XI-23.Относительное изменение температуры точки застоя Go / Go, » толщина, Y / x VRe 層状 3 3: Т、- Температура тормоза пограничного слоя, к, — диаграмма температуры тормоза свободного течения, XI-24.
Относительное изменение температуры тормоза Go / Go, » вся толщина турбулентности Пограничного слоя г! x 1 / Re * Moo-2.8 методика Ван рассмотрена, следовательно, на данном уровне знаний о механизмах передачи импульса и тепла в турбулентных пограничных слоях Дриеста должна считаться удовлетворительной.
Смотрите также:

