Оглавление:




Теплоотдача при поперечном обтекании труб
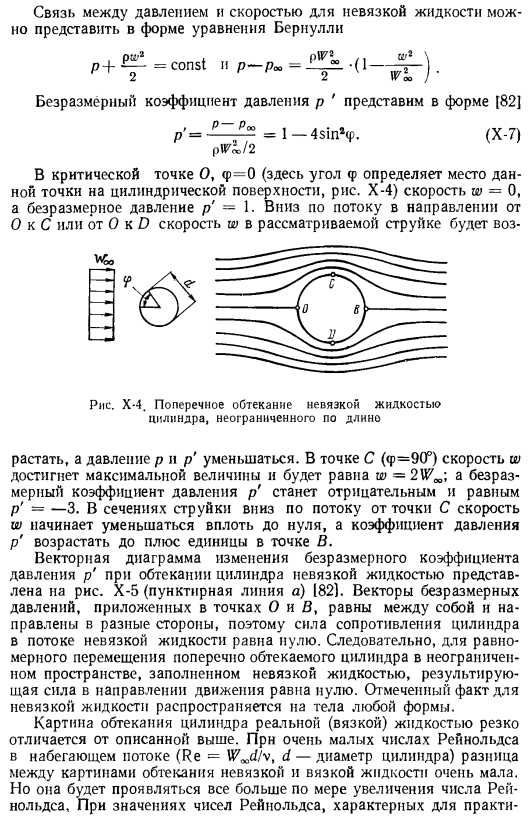
- В инженерной практике часто приходится определять теплопередачу поперечно очищенной трубы, так как она является элементом многих теплообменников. Гидродинамическая ситуация при обтекании трубы очень сложная, и, естественно, трудно судить о теплопередаче. Рассмотрим процесс обтекания невязкой жидкости вокруг круглой трубы. Рисунок X-4 показывает схему течения.
Проследим изменение гидродинамических параметров струйки, которая втекает в трубу в критической точке O и огибает цилиндрическую поверхность в направлении C и B. из этих величин на поверхности трубы через w и P. Связь между давлением и скоростью в невязкой жидкости может быть выражена в виде уравнения Бернулли пн£^.= const и п-пн = ^〜..(1— Безразмерный коэффициент давления p ’может быть выражен в следующем виде: [82] = л-4sin₽‘. (Х-7) РЛ / 2 .
Для многокомпонентной системы число термических уравнений состояния равно числу компонентов, например, для смеси идеальных газов эти уравнения состояния выглядят как . Людмила Фирмаль
В критической точке O, p = 0 (где уголp определяет положение этой точки на цилиндрической поверхности, рис. X-4), Скорость рассматриваемой струйки W возрастает по отношению к потоку D в направлении скорости w = O, безразмерного давления p = O или C или O. Рисунок Х-4.Поперечное обтекание цилиндрической невязкой жидкости неограниченной длины Увеличивается и уменьшается давление p и p’. в точке C(p = 90°) скорость u; достигает максимального значения и равна w-2^.
И безразмерный коэффициент давления p ’ становится отрицательным и равен p. In на участке струйки вниз по течению в точке C скорость w начинает уменьшаться до нуля, а коэффициент давления p увеличивается до плюс 1 в точке B. На рисунке показана векторная диаграмма изменения безразмерного коэффициента давления p ’при обтекании цилиндра невязкой жидкостью. Х-5 (ломаная линия а) 182].Безразмерные векторы давления, приложенные к точкам O и B, равны друг другу и направлены в разные стороны, поэтому сила сопротивления цилиндра в потоке невязкой жидкости равна нулю.
Таким образом, равнодействующая сила в направлении движения равна нулю для того, чтобы равномерно перемещать боковой обтекаемый цилиндр в неограниченном пространстве, заполненном невязкой жидкостью. Примечательный факт невязкой жидкости распространяется на объекты любой формы. Схема реальной (вязкой) жидкости, обтекающей цилиндр, существенно отличается от описанной выше. При очень малом числе Рейнольдса набегающего потока(Re = W ^ d / v, где d-диаметр цилиндра) разница между режимами течения невязкой и вязкой жидкостей очень мала.
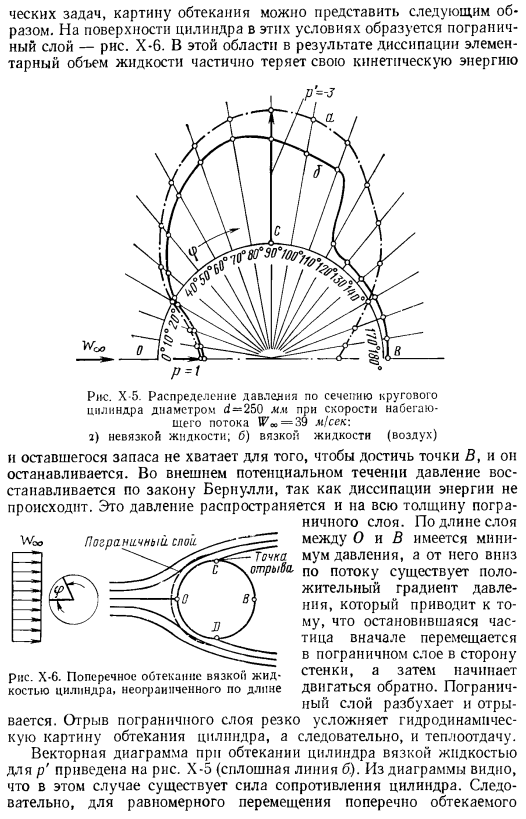
Но по мере увеличения числа Рейнольдса оно становится все более ощутимым. Для задач картина течения может быть представлена следующим образом: при этих условиях на поверхности цилиндра образуется пограничный слой-рисунок X-6.In в этой области в результате диссипации элементарный объем жидкости частично теряет свою кинетическую энергию. Рисунок Х-6.Боковое обтекание цилиндра вязкой жидкости неограниченной длины Рисунок Х 5.
Распределение давления по поперечному сечению цилиндра диаметром d = 250 при скорости набегающего потока И⁷00= 39 м / с: 2) невязкая жидкость; 6) вязкая жидкость (воздух) Оставшегося инвентаря недостаточно, чтобы добраться до точки Б, и он останавливается. При внешнем потенциальном потоке давление восстанавливается по закону Бернулли, так как рассеивание энергии не происходит. Это давление распространяется на всю толщину пограничного слоя.
Это приводит к тому, что существует минимальное давление по длине слоя между О И В, а от его нижнего течения возникает положительный градиент давления, который приводит к тому, что взвешенные частицы сначала перемещаются в пограничном слое в сторону стенки, а затем начинают возвращаться. Пограничный слой расширяется、 Именно поэтому отрыв пограничного слоя резко усложняет гидродинамическую ситуацию обтекания цилиндра и, как следствие, усложняет теплообмен. векторная иллюстрация течения вязкой жидкости вокруг цилиндра P’. Х-5 (непрерывная линия B).
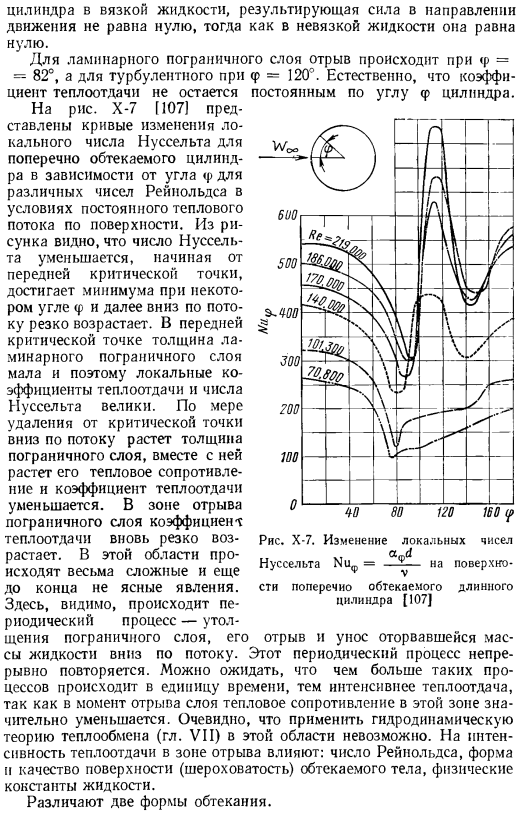
На рисунке видно, что в этом случае имеет место сопротивление цилиндра. Поэтому для равномерного бокового движения потока Угол φ постоянная цилиндра. 160(С. Рисунок Х-7.Локальное изменение числа нуссельта, если = — на длинной поверхности, обтекаемой сбоку Цилиндр[107J Для цилиндра в вязкой жидкости сила, создаваемая в направлении движения, не равна нулю, но равна нулю в невязкой жидкости. В ламинарном пограничном слое разделение происходит приp = 82°и при = 120 ° в турбулентном потоке.
Конечно, никакого коэффициента теплопередачи не остается Рисунок X-7 [107] воспроизведение Построена кривая изменения локального числа карбонукерта бокового обтекаемого цилиндра, зависящая от углаp различных чисел Рейнольдса при постоянном тепловом потоке на поверхности. Из рисунка видно, что число нуссельта начинается в передней критической точке, достигает минимума под углом φ, а затем быстро увеличивается дальше downstream. At передняя критическая точка, толщина ламинарного пограничного слоя мала, что приводит к большому локальному коэффициенту теплопередачи и числу нуссельта.
При удалении от нижней критической точки увеличивается толщина пограничного слоя, что, в свою очередь, увеличивает тепловое сопротивление и снижает теплопередачу coefficient. In в зоне разделения пограничного слоя коэффициент теплопередачи резко возрастает again. In в этой области происходят явления, которые очень сложны и еще не до конца ясны. Здесь, по-видимому, происходит периодический процесс-утолщение пограничного слоя, вытекающей из него жидкости.
- Этот периодический процесс повторяется continuously. At в момент разделения слоев тепловое сопротивление этой зоны значительно снижается, поэтому чем больше таких процессов происходит за единицу времени. Тем интенсивнее ожидается теплообмен. Очевидно, что в этой области гидродинамическая теория теплопередачи (гл. VII) невозможно применить. На прочность теплообмена в зоне разделения влияют число Рейнольдса, форма и качество (шероховатость) поверхности обтекаемого тела и физические константы жидкости. Есть 2 формы потока. Отделение и удаление разорванной матери 1-й выполняется с числом .
Рейнольдса Re 2•10s, с малым углом отрываp, равным приблизительно 82°и отличающимся большим цилиндром resistance. In в этом случае течение в пограничном слое остается ламинарным до точки отрыва и становится турбулентным downstream. As число Рейнольдса Re > > > 2•10⁵ увеличивается, точка перехода от ламинарного пограничного слоя к турбулентному слою движется вверх по течению, и по мере увеличения числа Рейнольдса она входит в область непрерывного течения.
Для каждой конкретной термодинамической системы её уравнение состояния определяется из опыта или методами статистической механики, и в рамках термодинамики оно считается заданным при определении системы. Людмила Фирмаль
В этих условиях на поверхности цилиндров в области непрерывного течения наблюдаются как ламинарные, так и турбулентные пограничные слои. Первоначально она начинается от предыдущей критической точки и на определенном расстоянии от нее идет вниз по течению до 2-й критической точки, где разделение происходит уже в области турбулентного пограничного слоя. При дальнейшем увеличении числа Рейнольдса возникает кризис течения-точка разделения перемещается вниз по течению. 2-я форма течения приблизительно равна Re 5•10 чисел и характеризуется большим углом отрыва cp (приблизительно 120°), расположением точки отрыва в области турбулентного пограничного слоя и низким цилиндрическим сопротивлением потока.
Обратите внимание, что по мере движения точки разделения вверх поток постепенно перестраивается. расположение точки p = 120°соответствует полностью развитой форме течения. Первая форма течения называется подкритической, а вторая-сверхкритической. На рисунке х-7 показаны измерения подкритической области, а большое число Рейнольдса соответствует началу переходного кризиса. Первым минимумом числа нуссельта на рисунке является X-7, что соответствует точке разделения пограничного слоя.
При расчете теплообменника необходимо знать среднее значение коэффициента теплоотдачи по длине трубы, которая обтекается под углом Ф и в поперечном направлении. На основе обработки экспериментальных данных цилиндров, которые были рационализированы в поперечном направлении воздуха, воды и трансформаторного масла, была получена следующая формула[29]: Дата и время, — 5-г 1 * 103 Nu,= 0.50 Re° Rg⁰, 3 (R Leu / R Leu.)⁰, 2⁵(X-8) И Re = 1•1034-2-10⁵ Nu; = 0.25 Re»’rrg,°» (R17 / RGJ⁰’2⁵.(Х-9).
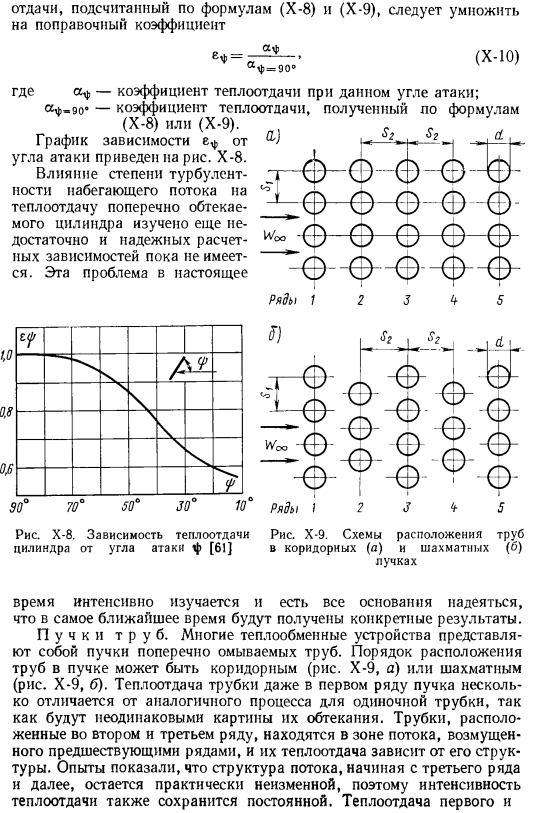
Приведенное выше уравнение подходит для подкритического обтекания цилиндра. Сверхкритическая область мало изучена, и достоверные расчетные зависимости пока отсутствуют. Если угол столкновения между встречным потоком и цилиндром (называемый углом a и t и f) отличается от 90°, то тепловой коэффициент Необходимо умножить отдачу, рассчитанную по формулам (х-8) и (Х-9), на поправочный коэффициент (Х-10) ^ = 90° Здесь-коэффициент теплопередачи при заданном угле атаки. c ^ — eo ’ — коэффициент теплопередачи, полученный по формуле (X-8) или(X-9). График угла атаки показан на рисунке. Х-8.
Влияние степени турбулентности свободного течения на теплообмен поперечного обтекаемого цилиндра до сих пор не изучено, и достоверной расчетной зависимости нет. В настоящее время эта проблема (Л) Я… Рисунок X-8.Зависимость теплопередачи цилиндра от угла атаки[61] 11я. * 2 3 b 5 Строка 1 Рисунок Х-9.Расположение труб в коридоре (а)и балка шахмат (б) Время интенсивно изучается, и есть все основания ожидать ощутимых результатов в ближайшем будущем. Куча труб. Многие теплообменники представляют собой пучки труб, которые промываются сбоку.
Порядок расположения труб в пучке будет коридорным (рисунок х-9, А) или шахматным (рисунок х-9, Б).Даже если это первый ряд балок, теплопередача в трубе несколько отличается от аналогичного процесса в одной трубе, так как характер течения вокруг нее различен. Трубы во 2-м и 3-м рядах находятся в зоне потока, нарушенного предыдущим рядом, теплопередача которого зависит от его structure. In в ходе эксперимента было показано, что коэффициент теплопередачи также постоянен, так как структура потока после 3-го ряда практически не меняется.
Первая передача тепла и 2-й ряд трубок меньше, чем 3-й ряд. На процесс теплопередачи пучка влияют диаметр Tpy6d и их взаимное расположение S2 (рисунки X-9, a и 6). Исаченко В. П. А. 132] предложена следующая формула для определения коэффициента теплопередачи пучка труб: Nu, = Re «Pr, ⁰ -» (Pr / PrJ⁵ ’ 2⁵e e eₛ(x-11) Так… Эй, −10 ′ — Мистер хаб、 Рисунок Х-10.Зависимость угла атаки теплопередачи в пучках труб[61] Для шахматной связки c = 0.41 и n = 0.60. Для коридоров −0.26 и N = 0.65.
Внешний диаметр трубки определяет размер. Критерий Рейнольдса включает скорость, определяемую самой узкой частью пучка труб. Физические константы определяются средней температурой жидкости. Критерий Прандтля Rgsh обнаруживается при температуре стенки. Поправочный коэффициент e $учитывает влияние относительного расстояния SJd(рисунок X-9). Для рядов балок в глубоких коридорах Эс =(S₂/ д)» ⁰ » ⁰ ; Для шахмат Так… S, / S₂2е$ =(SJSJI *、 Так… Sₗ/Sₐ> 2eₛ= l, 12. В поправочном коэффициенте (х-11)учитывается номер строки.
Исследования показали, что при низкой турбулентности потока, падающего на балку, коэффициент Е / может быть принят равным в коридоре балки в следующих случаях: Первая строка Ej = 0,6、 2-й ряд r₂= 0,9, 3-й ряд e₃= 1,0. Соответственно на шахматной доске: Ej = 0,6, e₂= 0,7, e₃= 1,0. Формула (х-11) подходит, если угол между направлением протекающего потока и осью балочной трубы (углом атаки) равен Φ= 90°.Для других углов атаки необходимо ввести поправочный коэффициент e ^(X-10).Его значение видно из графика на рисунке. Х-10.
Смотрите также:
| Теплоотдача при вынужденной конвекции | Теплоотдача в жидких металлах |
| Теплоотдача при вынужденном движении жидкости в трубах | Теплоотдача при больших скоростях |

