Оглавление:



Теплоотдача в окрестности критической точки при взаимодействии осесимметричной турбулентной струи с пластиной, расположенной нормально к направлению скорости потока
- Представляет собой уравнение (VI11-27) в случае утечки осесимметричной струи, образованной разрезанным соплом диаметром dQ на пластине. Ню = 0.763 (VIII-61) Где Uj = y; x-расстояние от критической точки вдоль поверхности пластины до определенной точки(оси x).
Используя формулу (VIII-61), известен коэффициент соответствующего критерия ре-сопла=и расстояние h =от выхода сопла до препятствия (где h-расстояние от выхода сопла) до барьера, м). Зависимость= f(h)была определена экспериментально относительно случая утечки изотермического потока воздуха на пластину.
В справочниках термодинамических величин часто приводятся значения абсолютной энтропии при температуре 298,15 К, которые соответствуют увеличению энтропии при нагреве вещества от 0 К до 298,15 К. Людмила Фирмаль
Максимальная скорость воздуха на выходе из сопла эксперимента не превышала 100 м! sec \эти зависимости являются 151:. 2 / i6、1,5-^ /1⁽ «22.⁾、 6 A ^ 16,₌16.1 / ₀ (VIII-62) Мы объединяем (VIII-61) и (VIII-62), чтобы получить формулу, которая определяет коэффициент теплопередачи (Pg = 0,7), когда осесимметричная струя течет через пластину. — пп0. Пять Для 2 A 6, Nu = 0.935 6 7и 16, ню = 3.06-м ^ пр° Ло.77. (VI С-63) Куда? Будь Песней= Диаграмма VIII-4.
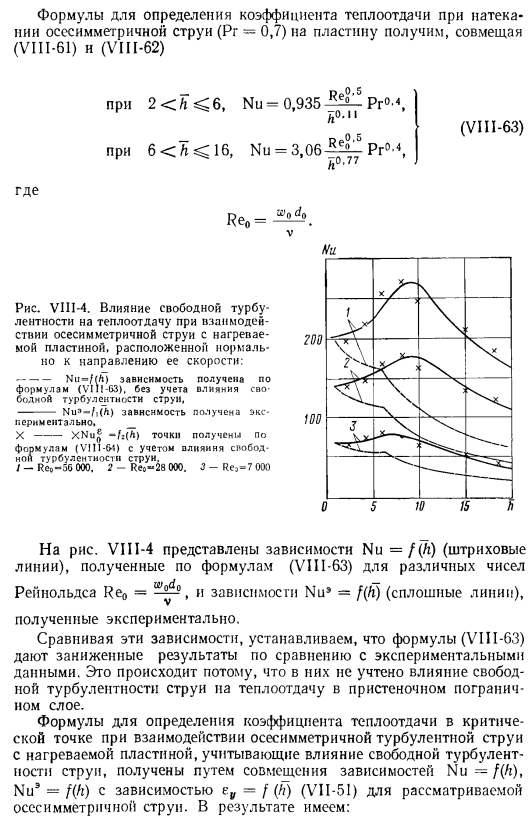
- Влияние свободной турбулентности на теплообмен при взаимодействии осесимметричной струи с нагретой пластиной перпендикулярно направлению ее скорости: * — — — — — — Nu = /(ft) зависимости берутся из Уравнение (VI11-63), исключающее влияние турбулентности свободной струи、 ——- Nu » — / i (h) зависимости получены экспериментально. X — — — — — — XNu -/: (L) точка Формула, учитывающая эффекты свободно охлаждающей турбулентности (V111 — &1). Я— Re₉-5г ООО. 2-реп-28 ООО. 3-Ре;> = 7 ООО.
Энтропия, обращающаяся в нуль при абсолютном нуле температуры, называется абсолютной энтропией. Людмила Фирмаль
На рис. VIII-4 показана зависимость Nu = f (пунктирная линия) и экспериментально полученная зависимость Nu⁵= f (h) (сплошная линия), полученная при различных числах Рейнольдса RE-^-°формулы (VIII-63). Сравните эти зависимости и установите, что формула (VIII-63) дает заниженный результат по сравнению с экспериментальными данными.
Это связано с тем, что мы не учитываем влияние свободной турбулентности струи на теплообмен в пограничном слое вблизи границы. Приведена формула для определения коэффициента теплопередачи в критической точке при взаимодействии осесимметричной турбулентной струи и нагретой пластины, учитывающая влияние свободной турбулентности струи, зависимости Nu = / (/1), Nu3-f (h) И зависимости EF = f ( / / ) (VII-51) в случае осесимметричной струи под действием consideration. As в результате, вы можете: 2 h ^ 6 .
Так… Ну «= 0.935(1 +0.00197ft1 ’⁷⁵Reo’2⁴) Пр1’2⁴; 6 м 16、 NuJ = 3.06 — ^(1 + 0.0197 ft° ’resre?’2⁴) ⁴ пр°’ху * (VI11-64) Куда? Формула (V1II-64) эффективна для 7-10°re₀ 5. 6-10 мкг и Pr = 0,7. Отметим, что расчетную зависимость для определения коэффициента теплопередачи в критической точке при взаимодействии осесимметричной струи с препятствием можно получить, используя ту же гипотезу, что и вывод уравнений плоской струи (VIII-59) и (VII1-60). в этом разделе мы выведем формулу, используя другой, более простой метод(VIII-64).
Смотрите также:

