Оглавление:









Теплоотдача в окрестности критической точки при взаимодействии плоской турбулентной струи с пластиной, расположенной нормально к направлению скорости потока
- В более общей постановке, чем условия (viii-2, vii1-3), рассмотрим, как ламинарный поток 2-мерного потока решает гидродинамические задачи, когда ось течет в цилиндр перпендикулярно оси потока. Напомним, что при решении гидродинамических задач на основе (vip-2, vii1-3) полученные результаты справедливы только для небольших участков течения вблизи критической точки.
Рассматриваемый метод предложен г. Блазиусом и К. Хименном и Л. Улучшен Ховартом [188]. Выберите следующую систему координат. Ось y направлена от критической точки к потоку, а ось x расположена вдоль потока распространяется через барьер. Скорость на внешней границе пограничного слоя выражается степенным рядом по отношению к переменной wi = 1cx 4-и ₃ x * 4-u. X⁵4 -. 。 (viii-32).
Нулевое значение температуры служит реперной точкой для построения термодинамической шкалы температур. Людмила Фирмаль
Здесь, iii, from, u₅,. .является фактором, который зависит исключительно от формы body .In наша задача, они подлежат определению .Если учесть (VI1-11) и умножить ряд на его производную, то получим: —— ■^=£₎₎^-, =ᵤ? .В + 4″ ₁ » Х1 .r₅ (6u₁u₅+3ᵤ2) + .. , (viii-33) Уравнение неразрывности аналогично выражается в виде степенного ряда, но интегрируется путем введения функции потока φ (x, //), коэффициенты которой зависят от y. Однако эти функции коэффициентов y не должны зависеть от коэффициента y, заданного профилем тела.
При этом условии функция коэффициента становится универсальной, зависящей от y, и подходит для любой формы обтекаемой линии object. As в результате, он подходит для пластин, которые размещены по всему потоку. Для распределения скоростей в пограничном слое был найден ряд, в котором функция коэффициента оказалась универсальной[881.
Для текущей функциональности см. Раздел φ= j / — ^ — [hjхД (l) 4-4 ′ ₃33 / ₃ (l) + f₅ (l) 4 — l (vi11-34) Куда? Безразмерные координаты. Для компонентов скорости wx и wx были получены следующие ряды: (viii-35) — /•£[«, А + 12В, Х7, + 30′, х » А4. .b (VIII-36) Где простые числа Следующие системы обыкновенных дифференциальных уравнений были получены путем объединения уравнений движения (VII1-1), уравнения (VIII-33), уравнения (VIII-35) и уравнения (VII1-36) . / ; Ч1/; = 14 .(VII1-37).
Здесь приведены только 2 формулы для определения коэффициентных функций D и/ the .In в дальнейшем только первые 2 члена используются в формулах (VIII-32), (VIII-34), (VIII-35), (VIII-36) для соответствующих строк .Форма граничного условия системы (VIII-37) выглядит следующим образом: А = в = 0, Ф3 = Ф3=°, .. При t) = 0; a =! 。 А = — п пр » ч =°°- (viii-38) Система уравнений (vip-37) и граничные условия (viii-38) решаются численно. Следовательно, если известны коэффициенты uₗₜ и -,. 。.
То гидродинамическая задача может быть solved. In другими словами, wx и Для определения теплопередачи необходимо решить уравнение энергии (ВИП-16), используя для этой цели результаты решения гидродинамических задач. Распределение температуры по толщине теплового пограничного слоя может быть выражено в виде следующего ряда 11131: 0 (x, 0 = l (’1) + — x’a₂ (’1′) + 1yao1w уй + — x’f₄ (n) + -. (viii-39) 1. Вот, foₜf₂. .Is универсальная функция коэффициента, которая не зависит от коэффициента, ₃, .. Зависит от числа Прандтля.
Чтобы определить эти функции, получим следующую систему дифференциальных уравнений. ^; + л ^ = о (viii-40) Граничное условие: £ » = £, = 0 для h = 0, 1 (ush-41) fₒ= i, f₂= 0] = oo для m. J (viii-40) функция h такая же, как (vip-37). Система уравнений с граничными условиями (viii-41) (viii-40) решается численно[113]. Формула для определения локального теплового потока к стенке с учетом (viii-39) и формула для l (vi11-6) могут быть выражены в следующем виде: Кя (х) — ды Х [ф; (0) + — ^x2f; (0) + ф; о) + (viii вида-42) Луиджи. Тепловой поток также может быть выражен в другой форме: qw (x) = a (tw-tcₐ). (viii-43).
Если правая сторона (viii-42) и (viii-43) равны, оставляя только 2 члена столбца、 (viii-44) Коэффициенты f ’ (0) и f’z (0), необходимые для расчета по формуле (vi11-44), указаны в[113]. Если число Прандтля pr = 0, 7, то эти коэффициенты равны ФДЖ = 0. 496, Ф ’= 0. 448. Представим коэффициент теплопередачи а в безразмерном виде Ну = ^ = 6ₒ / / я- [о, 496 + 0. 448 — ^ — х» +. .[ .. (viii-45) Как уже говорилось, их коэффициенты uₛ. 。 。Это зависит от формы обтекаемого тела и скорости набегающего потока.
Рассмотрим взаимодействие струи с пластиной, которая расположена перпендикулярно направлению ее скорости. Скорость струи жидкости, вытекающей из сопла уменьшается по длине струи в результате ее взаимодействия с окружающей средой. Следовательно, их коэффициенты, и₃,. 。 。При взаимодействии струн и препятствий расстояние между выходом сопла и препятствием будет иметь различные значения в зависимости от h. При определенных условиях величины uₗf и₃,.
Определились experimentally. As в качестве примера приведем выражение для определения значений uj и₃. 。Условия: плоский поток воздуха, образованный различными соплами (ширина щелей l0 = 5, 5 мм, 10, 4 мм, 15, 2 мм, длина щелей l = 135 мм) и плоскими препятствиями, вытекающими из сопла с разной скоростью; см. Номер повторного сопла на выходе из сопла. Она колебалась в диапазоне от 18, 000 Ре ^ 90, 000.
Максимальная скорость истечения воздуха из сопла не превышала 80 л / с; температура струи на выходе из сопла поддерживалась равной температуре окружающей среды. Эксперименты, проведенные в указанных условиях, показали сечение струи длиной от h = 0 до h = 6, 5 (где h =безразмерно Расстояние от выхода сопла до препятствия’) расход воздуха остается постоянным и равен расходу (на выходе из сопла).
- Для определения безразмерной скорости в сечении 6. 5 h 16 длины струи (где скорость потока уменьшается) была получена следующая экспериментальная зависимость: Вт _ 2. 54 часов (viii-46) Где ww-среднее значение скорости потока по оси струи (ось y совпадает с осью струи). Для того, чтобы определить их коэффициент. 。Необходимо знать закон изменения скорости на внешней границе пограничного слоя (вдоль оси x). Он образуется при расширении воздуха на пластине.
Эксперименты показали, что скорость на внешней границе пограничного слоя wj изменяется от нуля до максимума в критической точке. w * значение расстояния от it. In площадь пластины длиной o — 1, скорость увеличивается от нуля до w*, а давление падает от максимального до атмосферного давления. Область течения стен-двигателя которая ограничена до меньш чем 1 в размере вызвана областью.
Нулевые значения температуры и энтропии при абсолютном нуле приняты как удобные соглашения для устранения неоднозначности в построении шкалы для термодинамических величин. Людмила Фирмаль
Градиентные схемы течения; здесь происходит наиболее интенсивный теплообмен, поэтому исследования в этой области очень практичны. Определен закон изменения скорости на внешней границе пристенного пограничного слоя в пределах градиентной области течения experimentally. In диапазон расстояний от выхода сопла до пластины 2 l 14, этот закон принимает вид: 2? Я₌2-1, 6 | — У-Ф-0. 6 ф-ш, х, к Х, / Х、/ (viii-47) Для определения скорости w *и координат экспериментально были получены следующие зависимости: 2 ft 7, — ft -«. »», i = l, 9ft+» -«⁷; (viii-48) Для 7 ft 14, — ^ = 2, 52 ft-. », ^ — =0, 34 фута»». (vi1i-49) Да.
Сравните (vi11-32) и (vi p-47), чтобы определить требуемый коэффициент (vi11-50) Знать количество u₃, u₅. 。 。Кроме того, по формуле (vi Р-45) можно рассчитать коэффициент теплопередачи при взаимодействии струй и препятствий. Сравнивая значение коэффициента теплопередачи, рассчитанного по формуле (vi Р-45), с измеренным значением, мы обнаружили, что при определенных условиях последнее в 2 раза больше первого.
Такие большие различия в расчетных и измеренных коэффициентах теплопередачи позволяют предположить, что влияние свободной турбулентности в набегающем потоке газа на процесс теплопередачи в пристенном пограничном слое является ответственным. Различают турбулентное течение стенки, которое возбуждается неподвижной стенкой. Стена оказывает определенное влияние на турбулентность, что приводит к свободной турбулентности, которая возникает в отсутствие твердого тела wall. As в результате взаимодействия струпьев с окружающей средой возникает свободная турбулентность в струе. Турбулентность в струе анизотропна.
То есть его систематические особенности зависят от направления. Влияние турбулентной пульсации скорости протекающего газового потока на теплообмен в зоне взаимодействия потока с твердым телом было установлено в 1939 году в нашей стране[231. Влияние турбулентности на теплообмен при взаимодействии плоской пластины и турбулентной струи .
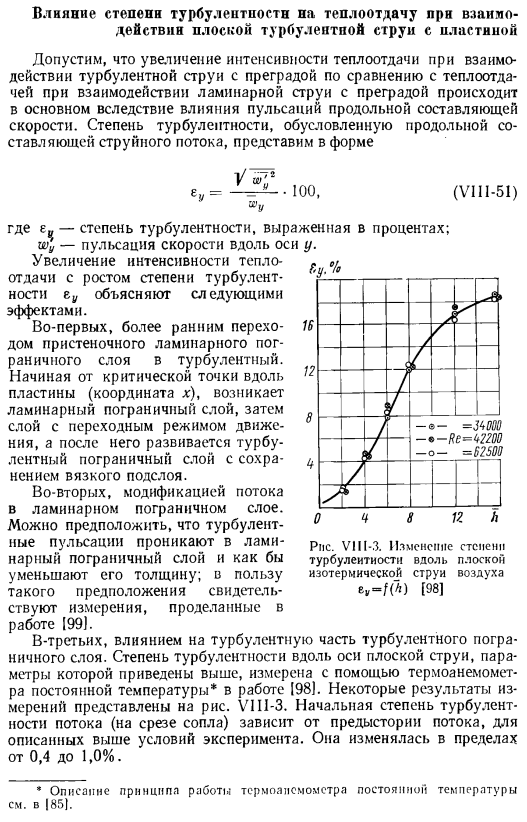
По сравнению с теплопередачей при взаимодействии ламинарных струй с препятствиями, предполагается, что увеличение интенсивности теплопередачи при взаимодействии турбулентных струй с препятствиями происходит в основном за счет пульсирующего воздействия продольной составляющей скорости. Степень турбулентности за счет продольной составляющей струйного потока может быть выражена в следующем виде: (v1i1-51) * 100、 Так. .Вот, €выражается в процентах, со степенью турбулентности . w * y-пульсация скорости вдоль оси Y .увеличение интенсивности теплообмена с увеличением турбулентности в gy объясняется следующими эффектами.
Во-первых, за счет начального перехода к турбулентному слою стенки бокового ламинарного пограничного слоя .Начиная с критической точки вдоль пластины (координаты x), отображается ламинарный пограничный слой, а затем слой с режимной областью перехода .Затем возникают турбулентные пограничные слои при сохранении вязкого подслоя .Во-вторых, путем изменения течения в ламинарной границе layer .It можно предположить, что пульсация турбулентного потока проникает в ламинарный пограничный слой и уменьшает его thickness .
To в пользу этого предположения свидетельствуют измерения, проведенные в статье 199 .В-третьих, влияние турбулентного пограничного слоя на турбулентные части .Степень турбулентности вдоль оси плоской струи, в которой приведены приведенные выше параметры, измерялась с помощью термоанемометра постоянной температуры*198) .Некоторые результаты измерений показаны на рисунке .VI11-3 .In в приведенных выше экспериментальных условиях степень первой турбулентности (на выходе из сопла) зависит от истории течения .
Она колебалась от 0, 4 до 1, 0% .£уу -■ Рисунок VII1-3 .Изменение степени турбулентности вдоль плоскости изотермического потока воздуха [98]] * Описание принципа работы цризмисмометра постоянной температуры см .в документе / 85 .Здесь выведена формула для определения коэффициента теплопередачи вблизи критической точки при взаимодействии плоской турбулентной струи с пластиной, перпендикулярной направлению ее движения .velocity .To для этого мы используем гипотезу о том, что путем введения дополнительного коэффициента вязкости в уравнение пограничного слоя можно учесть влияние свободной турбулентности набегающего потока на теплообмен в пристенном пограничном слое .
Согласно этой гипотезе, свободная турбулентность увеличивает вязкость пристеночного пограничного слоя .В работе [1110] предложена следующая зависимость от коэффициента, учитывающего дополнительную вязкость ЕА: е= kyuwᵤy、 (VIII-52) Где k-коэффициент пропорциональности, определяемый экспериментально .y-расстояние от поверхности пластины .Предположим, что коэффициенты, учитывающие дополнительную вязкость и дополнительную теплопроводность e₇, равны друг другу, то есть= e .
С учетом принятых допущений и обозначений система уравнений пограничного слоя, возникающего на пластине при обтекании турбулентной плоской струей, принимает вид: dwₓdwy ДХ делать (В VIII-53а, б, в) В соответствии с указанным Аналогично А ТВт-т (д) И затем (VIII-54) Система уравнений (VIP-53) принимает вид: Г2 — / » (/+«= (и -^) Л 4 .+О .₌ (VII1-55) Граничные условия системы уравнений (ВИП-55) могут быть выражены в следующем виде: для m] = 0, f = 0, f’= 0、0 = 0; —►°°、/ ’= 1、0 = 1。 (VI С-56).
Решение системы уравнений, содержащей граничное условие (VI P-56) (VII1-55), получено с помощью ЭВМ[PO, 98, 99] и имеет вид Pr = 0 .7 Ню =Re⁰ — ⁵ (0 .5 + 0 .164 б) .(VI11-57) Куда ?В состоянии, когда (выше) плоская струя течет навстречу препятствию, экспериментально получена следующая зависимость от uₜ .2 A 7、 7 ч ^ л4、- ₀ (VI11-58) Для вычисления значения b из соотношения (VIII-54) необходимо определить коэффициент пропорциональности k .сравнивая экспериментально найденный в критической точке коэффициент теплопередачи с рассчитанным по формуле (VI-57), получаем значение k = 0, 11 .
С учетом эффектов свободной турбулентности уравнения, определяющие коэффициент теплопередачи при движении плоской турбулентной струи к пластине перпендикулярно направлению потока, приведены в виде (VIP-57), (VIP-58) и (VIII-54) (3) .): Диапазон колебаний эталонного Re 1 .8-10 * re-T₀ 5-10⁴ и k = 0 .11 Для 2 h 7, Nu = 0 .5 — ^ X го° .°си X (14-0, 000, 035Л⁰ -regregee»), 7 л 14, nu= L, 9 — ^ x L⁰ х (1 + 0 .00024L⁰, 2ReS’eyey); (VI С-59) Диапазон колебаний эталонного Re 5-IO⁴Re 9-10⁴ и k = 0 .095 Если L 7, то Nu = 0 .5 ^ 4-x к l⁰ — ⁰ X (1 + O .OOZL⁰ Re Re ?’eeᵥ), 7 A 12, Nu = 1 .9-5 — ^ — x x (1+ 0 .0002°2 Re° — ⁵Ey) .(VIII-60) Для упрощения использования формул (VIII-59) и (VIII-60) критерий Рейнольдса, содержащийся в них, рассчитывался по выходному параметру сопла Re₀₀ .
Смотрите также:

