Оглавление:





Теплоотдача в окрестности критической точки при взаимодействии плоского ламинарного потока с пластиной, расположенной нормально к его направлению
- При взаимодействии ламинарного потока с пластиной перпендикулярно направлению ее скорости рассматривается процесс теплообмена вблизи критической точки O (рис. VII1-1).В этих условиях можно определить коэффициент теплопередачи!»В теории она определяется решением системы уравнений пограничного слоя с соответствующими граничными условиями. Вблизи критической точки допустима система уравнений следующего пограничного слоя-движение, непрерывность, энергия (В VIII-1а, б, в) вопрос.$ Д2 -•+wᵤ-= а —— ДХ у du2.
Здесь O-избыточная температура относительно температурной характеристики рассматриваемого процесса. consideration. As он приближается к поверхности, поток жидкости устремляется к препятствию, его кинетическая энергия уменьшается, а давление увеличивается. Кинетическая энергия жидкости в точке O (см. Рисунок VII1-1) равна нулю.
На внешней стороне пограничного слоя поток имеет потенциал(гл. VII) поскольку он рассматривается (без вязкости), мы можем описать его с помощью уравнений Эйлера. Людмила Фирмаль
Поскольку скорость в этой точке равна нулю, давление в критической точке (x-0) больше, чем давление в другой точке(x> 0).На тарелке. В точке o (рис. VII1-1), поток начинает расширяться и двигаться в направлении оси X вдоль поверхности, давление уменьшается, а скорость увеличивается Wₓ.Это означает, что существует градиент давления вблизи передней критической точки и, следовательно, градиент скорости.
Поэтому поток в этой области называется r = # 0^. Поскольку число Рейнольдса Re =мало в этой области, скорость Wскорость и координата X малы, предполагается, что поток жидкости ламинарный вблизи критической point. In кроме того, здесь действует отрицательный градиент давления, который также стимулирует ламинарное состояние.
Как показали исследования, градиент скорости оказывает существенное влияние на теплообмен в его возрастающем направлении, поэтому мы подробно рассмотрим это явление. Вблизи передней критической точки O вне пограничного слоя (см. рис. VII1-1) скорость U7X увеличивается вдоль оси x по линейному закону. №.x =U₁x, (V1II-2) Где uₜ-постоянная величина, которую можно рассматривать как градиент скорости.
Для скорости на внешней границе пограничного слоя формула (VIP-2) принимает вид: — Да. (VIII-3) (VII-11). Учитывая (VIP-2), это уравнение имеет вид «7Я^ =-4—= х DX dx1 Р Учитывая последнее выражение, уравнение движения (VIII-1a) можно выразить в виде: +(VIII-4) х ДХ у du1du2 ′ Закон распределения скоростей w и wпредставить можно выразить в виде: wₓ= ХF ’(ТДж), Вайоминг = — ф (г),(VI1I-5) Где f (y) — координатная функция y. f ’(y) — 1-я производная функции/(//) относительно y.
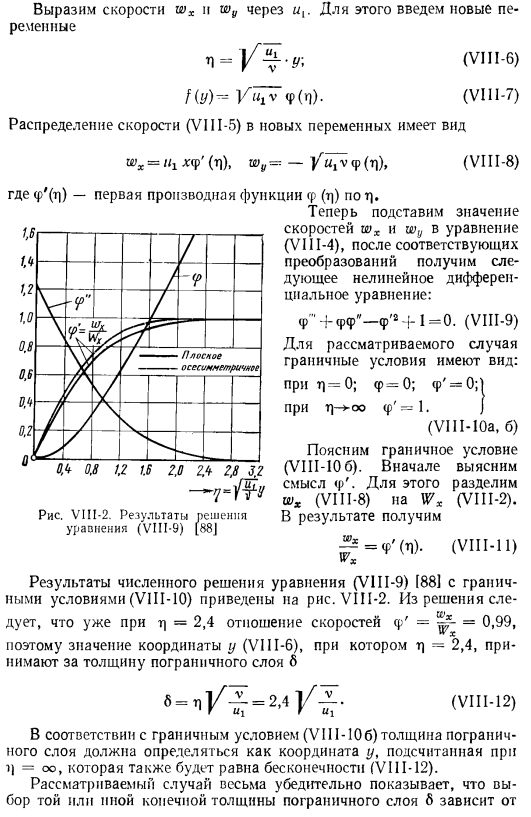
- Если подставить зависимость (ВИП-5) в уравнение неразрывности (в VIII-16), последние изменения в личности. Другими словами, (VI11-5) переходит в решение (в VIII-16).Таким образом, уравнение (VIII вида-4), которые могут быть использованы для определения функции ф(г), является только 1. Выразите скорость wₓ и wy через Для этого введите новую переменную F(Н). (VII1-6) (VIII-7) Форма распределения скоростей новых переменных (VI P-5) имеет вид WX и = «я(н)> лы {/=- ВВВ ф(Н)、 (VIII-8) Где φ*(τ|) — 1-я производная функции φ (τ]). Диаграмма VIII-2.
Результат решения уравнения (VIII-9) [88 | Здесь подставим значения скоростей wₓ и wy в уравнение (VII1-4) и, выполнив соответствующие преобразования, получим следующее нелинейное дифференциальное уравнение. φ — ’+φφ »- φ ’ * 4-1 =0.(VIII-9) рассматриваемое граничное условие имеет следующий вид: forn= 0;φ= 0;φ ’= 0; | as T | — > 00 f ’ = 1.) (VIII-10a, b) Поясним граничные условия (VIII-I06).Сначала найдем значение φ’. для этого разделим wₓ (VIII-8) на Wₓ (VIII-2). в результате、 ^ =Φ ’(Γ)). (VIII-11) .
В соответствии с граничным условием (VIII-10b) толщина пограничного слоя должна определяться как координата y. Людмила Фирмаль
На рис. 5 показано численное решение уравнения (VII1-9) 188]с использованием граничного условия (VII-10). VIII-2.Если m] = 2.4 уже, то отношение скорости φ ’ = ^ — = 0.99, поэтому значение координаты y (VII1-6) равно M] = 2.4 и принимается за толщину пограничного слоя. = 2,4]/^ -. (VIII-12) , которая вычисляется при 1)= oo, которая также равна бесконечности(VIII-12). Рассматриваемый случай заключается в том, что при выборе пограничного слоя 6 1 или другой конечной толщины、.
Точность, необходимая при определении скорости на внешней границе пограничного слоя. Как уже говорилось в разделе. VII, толщина пограничного слоя выбирается таким образом, чтобы скорость на его внешней границе составляла Wi = 0,99 \ VX. Переходим к решению уравнения энергии (VII1-1 c).Когда пластина нагревается в потоке газа, распределение температуры по толщине теплового пограничного слоя в этом случае имеет вид、 (VI1I-13) Где 0 = T-Tw-превышение температуры, толщина теплового пограничного слоя является переменной. 0 ^ = 7 ^ — Tw-избыточная температура падающего (не возмущенного) потока.
T-температура, изменяющаяся вдоль толщины пограничного слоя. Tw-температура стенки. Подставляя значение скорости (VIII-8) и температуру (VI11-13) в уравнение энергии (VII1-1 c), после соответствующего преобразования получаем следующее дифференциальное уравнение: Ф * + пр п ф ’=0.(VIII-I4) Граничное условие рассматриваемого случая имеет вид: для m] = 0 F = 0 для r | — oo G = 1. Решение этого уравнения: [1081 Куда? 1._ а (РГ) (VIII-15) (VIII-I6) для определения значения a (Pr) рекомендуется использовать следующую приблизительную зависимость: а (Рг) = х0.570рг⁰’⁴. (VIII-17).
Найдите формулу для определения числа нуссельта и Стэнтона. Для этого интегрируйте (VIII-17) с учетом (VIII-15, VII1-16) и выполните преобразование (известное из главы VII) И рассмотрение (VIP-2) Пи = 0.570 пр° ’⁴ ^ — ^ ⁵ м’ (VIII-18) Nu = 0,570 Rg °rere⁰ — ⁵ (VIII-19) Или St ^ 0.570 Pr — ° «keke -°’ ⁵ 、 (VIII-20) г / х Re = — — — — — — — — — критерии Рейнольдса. Формулы (VIII-I9) и (VIP-20) могут быть выражены в другой форме, которая содержит величину градиента скорости. Nu = 0,570 Pg° — Re » ⁰ — ⁵ (VIII-21) Или St =0,570 Pr-o — ⁶ ^ — ^j_⁰’rere7⁰’⁵, (VIII-22) Куда? Re»= -^; (VIII-23) В.
Скорость ненарушенного потока, который впадает в препятствие. Таким образом, в результате решения системы дифференциальных уравнений движения, непрерывности и энергии (V1II-I a, b, c) при соответствующих граничных условиях получена расчетная зависимость (для определения коэффициента теплоотдачи ламинарного потока плоского течения к пластине), которая расположена перпендикулярно в указанном направлении.
Смотрите также:

