Оглавление:








Гидродинамическое сопротивление и теплоотдача в трубах
- Поток жидкости в трубах Поскольку труба является элементом различных теплообменников, изучение процесса течения жидкости и теплообмена в трубе является очень практичным. При изучении течения и теплообмена в первом участке трубы возникают наибольшие трудности. Участок течения в трубе, где пограничный слой растет до тех пор, пока поле основного переменного значения (скорость или температура) не зависит от условий входа и поперечного сечения трубы, называется начальным участком.
В зависимости от характера процесса переноса гидродинамическая начальная секция и тепловая начальная секция 174 являются distinguished. In в первом разделе возможны ламинарные и турбулентные течения. При ламинарном и турбулентном течении (х = 0) в начальном сечении входного сечения трубы профиль скорости является плоским(имеет прямоугольную форму).
Однако здесь закон (VII-114)не справедлив, так как в стенках трубы и стенках пластины имеется ламинарно-текучий подслой, в котором действуют только ламинарные напряжения . Людмила Фирмаль
При ламинарном течении первого участка плоский профиль растягивается под действием сил трения, и на определенном расстоянии от входного участка он принимает и удерживается форму параболы (рис. VI1-12). В турбулентности начального сечения плоский профиль трансформируется под действием фрикционных сил forces. In область около стены имеет форму параболы, а в ядре потока она находится flat. In некоторые переходные зоны между стенкой потока и ядром, профиль скорости закрываются плавно.
Длина первого участка / начала трубы трубы с диаметром d в ламинарном потоке может быть определена по следующей формуле: / прошу = 0.03 Дж заново. (VI1-102) (VII-102) чем, Re =. при 5000 длина= 150 d. Первый участок трубы диаметром d в турбулентности / длина начала определяется экспериментально, а [88] / Топ » 25d40d. (В. Я-103) Трудно теоретически исследовать теплообмен в первом участке трубы.
Поэтому в этой главе мы рассмотрим теплообмен (x = 0) от входного участка по длине первого участка, где поток стабилизируется. Поток в трубе на расстоянии от входа называется стабилизированным потоком, так как поле скоростей фактически не зависит от характера распределения скоростей на входе. inlet. In в случае постоянного физического свойства жидкости при стабильном течении распределение скоростей поперечного сечения не изменяется по длине трубы.
Прогулка хорошо сбалансирована 1 А Г П2 З’, ’ с х. 1} 1? 2 ′ еще /.’Ы / ’/ г、 1. Рисунок VII-13.To вывод формулы (VII-104) Сопротивление жидкости Введем понятие коэффициента сопротивления. Когда жидкость двигает через трубу в результате диссипации энергии, давление drops. In площадь стабилизированного потока, выберем участок трубы с радиусом r длины I(рис. VII-13).
Цилиндрический объем жидкости между секциями 1-1 и 2-2 обусловлен отсутствием сил инерции. Потому что на него действуют давление и сила трения、 (П — п. Jr22= Т w2nrl、 Откуда? (VI1-104) Полученное уравнение справедливо для ламинарных и турбулентных течений в трубах. С его помощью определяют напряжение сдвига, действующее на стенку трубы в соответствии с заданным или измеренным перепадом давления. Здесь отметим относительную простоту экспериментального определения тангенциального напряжения m / экспериментального напряжения на стенках труб, возникающего при турбулентных течениях.
Даже при такой простой форме, как пластина, гораздо сложнее экспериментально определить тангенциальное напряжение с помощью внешнего обтекания тела. Таким образом, закон турбулентности часто изучается на примере движения жидкости в трубах. Падение давления обычно связано со средней скоростью: = L, ЗА _L, ЗА I d 2 P (VI1-105) Где£ — безразмерный коэффициент сопротивления*. UZcₚ-средняя скорость поперечного сечения трубы. а диаметр трубы. При сравнении уравнений (VI1-104) и (VII-105)、 т «> = г ptt⁷ п Или 8ТВ. (VI1-106) Сравните коэффициент лобового сопротивления с ранее введенным видом понятия среднего коэффициента трения Cf. 1RK ’ ЕР .
Если сравнить эту формулу с (VII-106)、 (VI1-107) Для ламинарного течения коэффициент сопротивления получается путем решения уравнения Навье-Стокса equations. As в результате решения распределение скорости в трубе представляет собой параболу, а коэффициент£равен (VI1-108) Уравнения Навье-Стокса для ламинарного течения несжимаемой жидкости в трубе основаны на совместном решении системы непрерывности и энергии. Ню= 3,65. (VI1-109) В случае турбулентности еще не удалось аналитически найти зависимость коэффициента сопротивления£от параметров потока, как это было сделано в случае ламинарного течения (VII-108).
Экспериментально найденная формула для определения коэффициента сопротивления турбулентной жидкости в трубе Красный= — ^ =(5-r 100). 103.、 ^ = 0,316 (красный) ⁴ — Формула (VI1-110) является содержанием закона браджианской толерантности. Позже был проведен эксперимент по определению коэффициента сопротивления а большого числа Рейнольдса с числом Рейнольдса более 10, и было показано, что формула (VI1-110) дает заниженный результат в этих условиях. Закон распределения скоростей поперечного сечения трубы найден экспериментально и может быть представлен в виде: (VII-111) число\ R J Куда? / 1 = 6 Re =40-103; Re = 110-JO3 и n = 7. Ре =3240-103 и N = 10.
Представленные данные показывают, что показатели уравнения (VII-111) мало зависят от числа Рейнольдса. Прандтль показал, что существует внутренняя связь между браджианским законом сопротивления (VII-110) и распределением скоростей (VII-111).Этот очень важный факт используется в теоретическом исследовании turbulence. In кроме того, указанное соединение позволяет получить экспериментальные данные по сопротивлению движению турбулентности в трубе при определении сопротивления продольно обтекаемой пластины с турбулентным пограничным слоем.
Используя закон сопротивления благиуса (VII-110), можно получить закон порядка 1/7 распределения скоростей J88J. = 8.74(^ у /⁷.(VII-112) Так, с одной стороны, закон 1/7 о распределении скоростей был получен экспериментально для некоторого значения числа Рейнольдса (Re =110-U3) (VII-111), а с другой стороны, закон 1/7 был получен некоторыми преобразованиями (теоретически) из закона Блазиуса. Это обстоятельство подтверждает существование внутренней связи между законом порядка 1/7 для распределения скорости и законом сопротивления брушиуса.
- Перепишите (VI1-112) с учетом обозначения формулы (VII-82) Ф =8. 74P1/’, (VII-113). Ранее был получен экспоненциальный закон для распределения скорости турбулентности вдоль пластины (VI1-83). Установлено, что если индекс 1/4 заменить на 1/5 или 1/6, то закон сопротивления Блазиуса (VII-I10) можно распространить на поток с более высоким числом Рейнольдса (Re >>10⁵). так, в Формуле (VII-113) индекс 1/7 заменяется на 1/8 или 1/9 и т. д. Значение C (n) изменяется следующим образом: n = 7 8 9 10 С(п)= 8.74 9.71 10.6 11.5 Так, при увеличении числа .
Рейнольдса уменьшаются показатели как закона сопротивления (VII-110), так и закона распределения скоростей (VII-113).Поэтому для очень большого предела числа Рейнольдса мы можем предположить, что существует асимптотический закон, который включает логарифмы в качестве пределов. Очень маленькая степень. Опыт подтвердил существование такого закона. Асимптотический закон имеет приоритет над степенным законом, поскольку его можно экстраполировать на любое большое число Рейнольдса, не имеющее экспериментальных данных.
Таким образом, универсальный закон распределения скоростей гладких труб с учетом констант, найденных экспериментально. Людмила Фирмаль
Ранее (§ 7, Гл. VII), используя полуэмпирическую теорию турбулентности, асимптотический логарифмический закон распределения скорости (VII-82) был получен в следующем виде: f (n)= A в l 4-Dl. При сравнении кривой универсального закона распределения скоростей (VI1-82) с экспериментальной кривой распределения скоростей в гладкой трубе、 Lx = — = 2.5 и D,= —1pr = 5.5、 Икс. для чего x-0.4 и 0.111, обе кривые хорошо подобраны. в (VI1-82), может быть выражен в следующем виде: p 01)= 2,5 в 4-5. 5. (В VII-114).
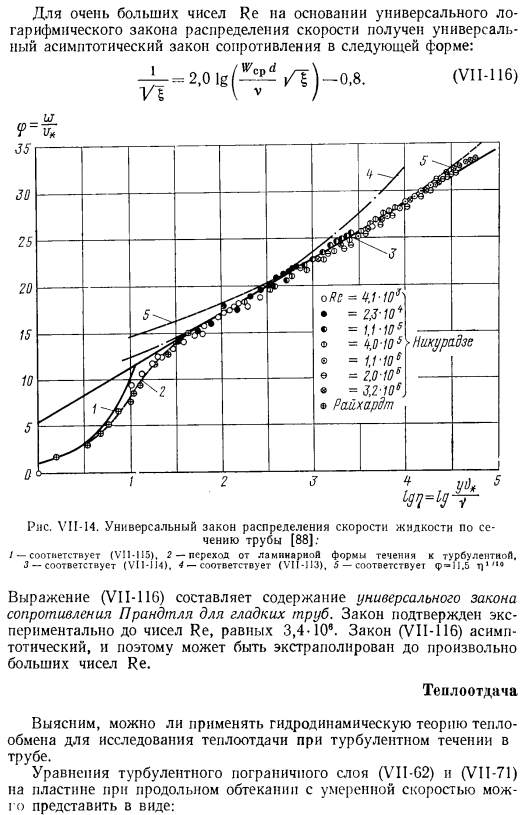
В полулогарифмических координатах зависимости (VII-114) являются прямыми линиями (рис. VI1-14). В выводе (VI1-83) учитывалось только турбулентное касательное напряжение, а ламинарное напряжение вообще не учитывалось. сдвига generated. By прямое измерение, в области слоистого подслоя、 F = t], (VII-115).
Это кривая, нарисованная на левой стороне рисунка в полулегарифметических координатах VI1-14. Между ламинарной и турбулентной зонами течения в трубе, а также имеется буферный слой при обтекании plate. In полулогарифмические координаты, распределение скорости этого слоя соответствует Кривой 2 (рис. VII-14). Мы обнаружили, что каждая из последних 3 зависимостей справедлива для соответствующего слоя жидкости. Границы этих слоев устанавливаются: Для ламинарных подслоев (VII-5) до 5 от стенки.
Для буферного слоя от = 5 до = 30; = Зона турбулентности от 30 до максимальной Ф / С ’. Возможные значения при заданных условиях〜 Для очень больших чисел Re, основанных на универсальном логарифмическом законе распределения скоростей, универсальный асимптотический закон сопротивления получается в виде: _ _ 2.01 г ^ / т) −0.8. И (VII-116) Бить ⁵ Диаграмма VII-14.Универсальный закон распределения скорости жидкости по сечению трубы[88]: / — Соответствует (VI1-I15), 2-переходу от основной формы течения к турбулентному течению. 3-соответствует (VII-IJ4).
Соответствует 4-(VII-II3), соответствует 5 — p = JI, 5 t、 7.、 л. 5-oRc = y, 1Ws> * = # — /0 * > Nicurs idse = 1.1-для iOS = 4,0 70 5 1.1 У6 е-2.0 ′ 10 * * = Я. 2-10С Уreihalt О Компании — — — — — — X 1 Представление (VI1-116) является содержанием универсального прандулярного закона сопротивления гладким трубам. Закон экспериментально подтверждает, что число Re равно 3,4-10.Поскольку закон (в VII-116) является асимптотическим, это можно экстраполировать на любой большое количество Ре. Тепловыделение Для изучения теплообмена в турбулентном потоке в трубе рассматривается возможность применения гидродинамической теории теплообмена.
Уравнения для турбулентных пограничных слоев (VII-62) и (VII-71) на пластине в продольном потоке при умеренных скоростях могут быть представлены следующим образом: Уравнение движения Если сравнить эти уравнения, то можно увидеть, что распределение скорости и температуры по сечению трубы аналогично при условиях Pr = =» = 1 и Prtb =-1.Используя аналогичные условия скоростного и температурного профиля, можно найти зависимость между коэффициентом теплопередачи и трением в следующем виде: СТ = — С. 21.
Теплообмен в трубе при турбулентности можно исследовать с помощью уравнений турбулентной границы layer. In при стабильном течении толщина пограничного слоя равна радиусу трубы, а скорость и температура внешней границы пограничного слоя равны скорости и температуре на оси трубы. Уравнение пограничного слоя цилиндрических координат с осью x вдоль оси трубы и осью y вдоль радиуса r может быть выражено следующим образом с учетом случая трубы O.
Уравнение движения Уравнение энергии Сравним эти уравнения и найдем, что Pr = v A a — = 1 и пр. GC-m — = 1, профиль скорости и профиль температуры fl q Дополнительный период 1 из-за влияния dp, тур в трубе не похож Уравнение движения——— П ДХ В результате ставится под сомнение возможность применения гидродинамической теории теплопередачи в данном случае. Однако исследования показали, что в сильно турбулентном потоке разница между скоростным и температурным профилями невелика (1221), и они похожи, а значит гидродинамичны Теория теплопередачи Намика.
Для потока в трубе отношение (VI1-58) остается действительным(например, st-fs). При рассмотрении (VII-107)、 (VII-107) и (VII-I10) формулы для определения теплопередачи в трубе для излучения St = J—°11G⁴ −3333⁹⁶ 8 8 (Rej), / ⁴ 〜(красный) 1 ’⁴ Или по следующей форме (VII-47): Ню-0,0396 (красный) ⁰ РГ РГ. (VII-I17) Красный 1•10⁵ (В VII-118) (ВИМ 19).
В заключение следует отметить, что в данной главе мы рассмотрим простейшие случаи неучтенного теплообмена в потоке вокруг пластины и в потоке труб. а) степень сжатия (p = const); б) температурная зависимость физических констант жидкостей; В) влияние числа Прандтля(Pr = 1, Prtb = 1); г)Влияние формы кузова и качества (шероховатости) промываемой поверхности; Влияние этих факторов на теплопередачу обсуждается в следующих главах.
Смотрите также:

