Оглавление:








Трение и теплоотдача в турбулентном пограничном слое
- Выведена формула для определения локального коэффициента трения турбулентного пограничного слоя на plate. To для этого сначала находят зависимость толщины динамического турбулентного пограничного слоя 6 от параметров течения жидкости. Ре.|- =Эта зависимость, 6tb = f (Reₓ), получена путем решения интегрального уравнения для динамического турбулентного пограничного слоя. т д (Wₐ,—wₓ) wₓdy=: Y, (VII-84) Да.
Где 6 ТБ-толщина границы динамической турбулентности Второй слой; =И / j-скорость набегающего потока, равная скорости на внешней границе пограничного слоя. Заметим, что зависимость, описываемая средней скоростью (VII-84), ничем не отличается от аналогии ламинарного пограничного слоя(VI1-19).Затем при решении (VII-84)символ усреднения опускается.
В этом выражении мы подставляем значение из (VII-85). в результате. Людмила Фирмаль
Для решения задачи (VII-84) необходимо выбрать функцию распределения скорости по толщине пограничного слоя w velocity = f (y) и подставить ее в Интеграл, как это было сделано при решении интегрального соотношения ламинарного пограничного слоя (VI1-19).Рассмотрим простейший случай умеренного числа Рейнольдса. Рис VII-10. 2-слойное (упрощенное) распределение скорости по толщине турбулентного пограничного слоя .
Скорость wₓ линейно зависит от координаты y. для простоты буферный слой между ламинарным и турбулентным слоями не является considered. In другими словами, используется двухслойная схема пограничного слоя. При допущениях кривая толщины программного слоя имеет закрутку на внешней границе ламинарного вторичного слоя (рис. VII-Y).Правая часть уравнения (VII-84) содержит касательные напряжения.
Это объясняется тем, что в случае ламинарного пограничного слоя уравнение Распределение скоростей г = 0 В рассматриваемом случае фактическая кривая распределения скорости по толщине подслоя ламинарного течения неизвестна, поэтому данный метод не подходит и требует использования экспериментальных данных. Следующая формула Блазиуса подходит для пластин. ТДА =0, 022р1Г’ >( I / 4 (В VII-85) 1f » > действительно для btb / числа Рейнольдса Re 10.
Найдите интеграл от (VII-84) до 1921 года и подставьте в него функцию распределения скорости (VI1-83 a). ДС » ТС. (В VII-86) Если сравнить (VH-86) и (VII-17 a), то по IVoo = ^ j мы знаем толщину потери импульса 6**. 6 «Ж =4⁸ * О — vⁱⁱ -⁸⁷> Где (VII-84)-тангенциальное напряжение, полученное из интегральных значений (VI1-86) и (VII-85). Когда вы дифференцируете и разделяете переменные, вы получаете дифференциальное уравнение 6 ^ 6d6TC = 0,235(VII-88).
После того, как вы определили, какой из них, вы найдете нужную толщину турбулентного пограничного слоя Предположим, что на передней кромке пластины образуется турбулентный слой, находим постоянную C{фактически в начале пластины образуется ламинарный слой, который становится турбулентным на определенном расстоянии от передней кромки(см. рис. VI1-8).Исходя из этого предположения, получаем x = 0 и bC = 0, поэтому C = 0. В обобщенных координатах форма последнего уравнения для C = 0 имеет вид & ТБД _ 0.37 х (Reₓ),/⁶* (VI1-89).
Теперь выведем формулу для определения локального коэффициента трения. Когда распределение скоростей ламинарного потока является линейным, его можно описать следующим образом: 、 В. 1Goo 6Тб на внешней границе ламинарного подслоя при y = bl скорость равна wx-baXL (см. рис. VII-1I). в этих условиях последнее выражение можно выразить в следующем виде: А. 1/ У3/ БТБ 0.0228 \、 В полученном уравнении легко записать 2 неизвестные величины, основанные на толщине ламинарного слоя 6 ₁ и скорости w (VI1-83 a) на внешней границе ламинарного слоя.
Если мы сравним последние 2 уравнения、 Извлечение и извлечение следующих 6 маршрутов от всех участников ^ ₌ ₁ , ₈₇₈(_l_y/⁴. Подставьте значение 6 ТБ (VI1-89) в результирующую expression. As в результате получаем уравнение, определяющее скорость на внешней границе ламинарного потока подслоя Используя кривую распределения скоростей (VI1-83 а) и формулу (VI1-90) по толщине пограничного слоя、 V2J2G =. 1tb6tb * \ / lmjj(reₓ)⁰1 ⁰ (В VII-91) В ламинарных коллатеральных слоях, как уже упоминалось, поскольку линейное распределение скоростей является приемлемым、.
В этой формуле мы подставляем значения (VI1-90) и (VII-91) изc’x₍ l. tFco $ ТЕРАБАЙТ (1?Пример)° ⁶ 。 。 Формула, полученная из (VI1-89).B представить. После простой трансформации、 ТШ = 0,0296 Р Предварительно и с обеих сторон полученного выражения Наконец мы получаем ГВС 0,0296 ИЭС»(Р^) ⁰2 ″ Локальный коэффициент трения определяется по последней формуле. (VI1-25) рассмотрение равно следующему 0LK2 (VI1-92) 1 (Ре*) ⁰2 в Выведем формулу для определения среднего коэффициента трения Cf. Сопротивление трению пластины шириной b по длине от 0 до x можно представить следующим образом: U(х) — б§для XW (х) DX、.
- О Где xw (x) — локальное касательное напряжение, действующее на пластину на расстоянии x от передней кромки. Найдите величину U (x)другим способом. Суммарный поток импульса в направлении x при продольном обтекании пластины (§ 2, гл. VII) равна сопротивлению трения пластины, которая увлажнена с одной стороны 1881.In в соответствии с этим§ 2, Ch. In случай турбулентного пограничного слоя, VII терабайт U(х)= ВР fwₓ)ды. 0. Сделать последние 2 выражения равны И (Х)= B [рН (х) DX = bpwₓ-у> Х)ды О, да. И когда соотношение (VI1-17 a) задано、 U (x)= 6p1P6 *(x). (VI1-93).
При re; >10⁷ результат, полученный по формуле (VII-95), начинает отличаться от измеренного результата. Людмила Фирмаль
Комбинацией (VII-93), (VII-87) и (VII-89) получена формула для импеданса пластины, увлажненной с одной стороны по длине / n ширине b 1 / = 0.037 Р \ ПМ I \ V (В VII-94) По определению, средний коэффициент равен Подставляя значение U в эту формулу (VI1-94), получаем: = 0.074 /(Ре) 1⁷⁵. (VI1-95) Закон турбулентного сопротивления трению Прандтля (VII-95)показан в виде кривой 2. ВИ1-11.Этот закон справедлив для следующего диапазона чисел Рейнольдса: 510⁵Rez I0⁷.Формула (VII-95) выведена в предположении, что турбулентный пограничный слой начинается у передней кромки пластины.
В этих условиях результаты измерений в диапазоне чисел Рейнольдса 5-10y Ker 10⁷ хорошо согласуются. В Rez 5-10 поток на пластине ламинарный, поэтому необходимо использовать формулу (VI1-28).Формула (VII-95) может быть изменена ввиду того, что фронт пластины имеет ламинарный пограничный слой, который становится турбулентным от передней кромки по длине xvr(см. Рисунок VI1-8).
Поправка определяется следующим образом: из общего сопротивления пластины вычитается сопротивление турбулентного слоя по длине HVR (VII-95), а вместо него добавляется сопротивление ламинарного слоя (VI1-28) той же длины. Поскольку турбулентное сопротивление больше ламинарного сопротивления, коэффициент сопротивления Cf пластины, в которой расположены ламинарный и турбулентный слои, будет меньше значения, рассчитанного по формуле (VII-95).
Опустите заключение * исправления, чтобы указать конечный результат. г, 0,074 А. * 1 (Re.) 1’rere / (VI1-96) Где A * — константа, соответствующая критическому Рейнольдсу number. It имеет следующие значения[88]: Reₓ>ₗₚ3-10⁶5-10y10⁹3-10В 1050 1700 3300 8700. При выводе формулы (VII-95) коэффициента сопротивления использовался закон 1/7 распределения скорости по толщине пограничного слоя (VI1-83 а). Приводится формула для определения локального cf и среднего CF коэффициента трения.
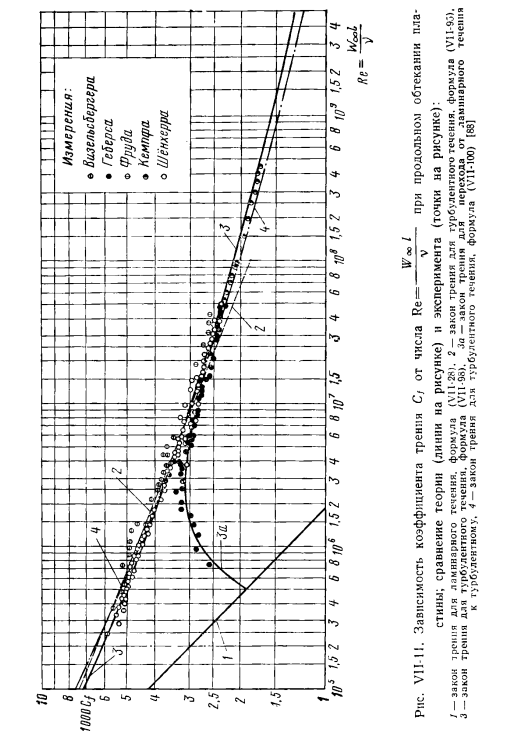
Это производная от которой использовались другие помещения. * Выводы см. в[88]. 10. Фу. Рис в VII-второй. Зависимость коэффициента трения CF на количество Ре= ————в этом случае окружающие продольным потоком Сравнение теории (линии на рисунке)и эксперимента (точки На рисунке): / — Закон трения ламинарного потока, формула (VI1-28). 2-Закон трения турбулентности, формула (V1I-95). 3-Закон турбулентного трения, формула (VII-98). Для-закон трения перехода от ламинарного течения к турбулентному. 4-закон турбулентности Гренни, уравнение (VI1-100) 183] .
При выводе формулы Прандтля-Шлихтинга мы использовали логарифмический закон распределения скоростей (VI1-82).Форма этих выражений является 7 =(2 lgReₓ-0.65) −23; r⁰>⁴⁵⁵ 1 (lgRe /)2 — ⁵⁸ ’ (В VII-97) (В VII-98) Закон сопротивления турбулентности в виде кривой 3 (VII-98) показан на рисунке 5. VII-11.Этот закон применяется к следующему диапазону чисел Рейнольдса: 10⁷CR ^ 10*. Если на лицевой стороне пластины имеется ламинарный пограничный слой, то формула (VI1-98) выражается в следующем виде: г. 0.455 __ я… * 1 (lgRe /) 2 ′ Re Re / (VII-98a) Где константа A * определяется так же, как и в Формуле (VII-96).
На рисунке показан закон сопротивления (VI1-98) перехода от ламинарного течения к турбулентному. VI1-11 3 а в виде кривой. Эта кривая была создана в 1700. Используя уточненный логарифмический закон распределения скоростей пограничного слоя на пластине, мы получили следующую формулу 1881. = 0,370 (logReₓ) _2’⁵⁸⁴; (VII-99) C,= 0,427 (logRe ₍- 0,407) −2,⁶⁴. (В VII-100) На рисунке показан закон турбулентного сопротивления в виде кривой 4 (VI1-100). VII-11.
В дополнение к кривой, представляющей закон сопротивления трению, VI1-111 показывает экспериментальные данные для сравнения(в виде точек). как видно, согласие между расчетными и экспериментальными значениями Cₛ является весьма удовлетворительным.
В случае продольного обтекания пластины, для определения коэффициента теплоотдачи или среднего а локального а, когда турбулентный пограничный слой начинается от ее передней кромки, можно поступить следующим образом: в зависимости от рассматриваемого условия, используя одну из формул (VI1-92, VII-95, VII-97, VII-98, VII-99 и VII-100) вычислить локальный С или средний коэффициент трения Cf. Полученное значение коэффициента трения присваивается формуле (VI1-74). Или.1 С. Вода pIFoc 2.
Смотрите также:

