Оглавление:










Уравнения турбулентного пограничного слоя
- Для турбулентного пограничного слоя (учитывается 2-мерное течение) и ламинарного пограничного слоя подставим их значения в виде непрерывности (Р-29, Р-30 и Р-31) и энергии (Р-52), средних значений и суммы пульсаций (49 А, В, С) вместо величин, содержащихся в уравнениях движения (Р-29).кроме того, на турбулентном пограничном слое выполняются несколько преобразований, анализ величины, малые уравнения движения, непрерывности и энергии разрушения.
Мы опускаем заключение 1881 года и приводим перечисленные уравнения. Уравнение движения (Ф= 0) для двумерного турбулентного пограничного слоя стационарного течения несжимаемой жидкости вдоль пластины. формат компонента x является + Р% — ^ = ±(pw>;). (VI1-59) Чтобы закрыть уравнение (VI1-59), введем Рейнольдса с последующим предположением, что члены, содержащие пульсирующие скорости w’X и w’y, пропорциональны среднему градиенту скоростиbX. — p ^ = L ^ — ^ Y(VII-60).
Такой круговой процесс называется процессом Томсона-Планка, и постулируется, что такой процесс невозможен. Людмила Фирмаль
Значение Lo называется коэффициентом турбулентной вязкости. Учитывая (VI1-60), уравнение (VI1-59)можно записать в другом виде ⁺- я (⁺»⁺Я(л->) Или p ^ ^ ₊ рч ^ = ± [(р ₊ л)^], (VII-62) Теперь обратим внимание на очень важную особенность турбулентности-пульсирующее движение скоростей w’x и w ’ ᵥ влияет на среднее движение скорости wₓ, поэтому вязкость увеличивается со средним motion. As в результате общую вязкость турбулентности можно считать суммой молекулярных вязкостей и суммой 2 величин дополнительных вязкостей, обусловленных турбулентностью.
Для сравнения приведем уравнение движения ламинарного пограничного слоя (VI1-10) (x-компонент).Дело-0 * Турбулентность, как правило, неустойчива, поскольку пульсация скоростей происходит непрерывно. Однако количественные характеристики потока принимаются как, например, среднее значение скорости, ее среднее значение wx. So, если среднее значение, например скорость a » x, не изменяется со временем, мы называем турбулентность устойчивой m.
Если сравнить уравнения движения турбулентного пограничного слоя (VI1-61) и ламинарного течения (VI1-63), то в первом члене появляется дополнительный член. Это явное напряжение или турбулентное тангенциальное напряжение несжимаемой жидкости. АНМ = п0 ( -^ -)= — п ’^. (VI1-64) Величина АО характеризует интенсивность импульса турбулентной передачи.
Предполагая, что перенос импульса молекул и турбулентность происходят независимо друг от друга, общее напряжение сдвига m можно выразить как сумму 2 величин: напряжения сдвига m вследствие межмолекулярных взаимодействий и напряжения сдвига reb вследствие взаимодействия отдельных объемов жидкостей макроскопического размера. Предполагается, что такие объемы возникают в турбулентном потоке. Они ведут себя как отдельные молекулы. Общее тангенциальное напряжение составляет mn = m +a₁ B=(u + D.) P^ -), (VII-65).
По аналогии с (VI1-9) вид уравнения движения турбулентного пограничного слоя в проекции на ось y имеет следующий вид: * £ — =0.Дю. (VI1-66) Уравнение неразрывности И затем Ди> х, dwy ДХ делать ДГ ’ ₓ-ДГ ^ ’у 0. (VI1-67) (VI1-67) показывает, что уравнение неразрывности выполняется как для средних, так и для пульсирующих скоростей. Уравнение энергии турбулентного двумерного пограничного слоя в несжимаемой жидкости、 (- ОРЧ; 0′) — р ^ х; (VI1-68) Если принять во внимание (VI1-60)、 — 00. 00 0/1 00\ -,. л \ / 0 ^ х \2И ⱼ»ⱼC₽₊рШрСр₌^) ₊₍₊и Л₎{ ^₊ + ± (- cplplfi&). (В VII-69) 0i. / Позвольте мне. — ЦПП ^ = ЛД’ -^ -’). (В VII-70).
Учитывая (VI1-70), формулу (VI1-69) можно переписать в виде p ^ p ^ + ^ CpA =±[₍X+ A)| -] ₊(И +οο) ( ^ ) g (U1b7). Уравнение (VI1-71) называется уравнением энергии турбулентного пограничного слоя. Для умеренных скоростей можно принять (n + A) ( -^) ’ = 0, и тогда из (VIb71) суммарный тепловой поток qₐ через турбулентный пограничный слой можно выразить как сумму теплового потока, возникающего в результате действия молекулярной теплопроводности на границе Q и qᵣ₆. 7н = ? +9₁б = (>.+Л) -^ -. (V1I-72) Величина Aq характеризует интенсивность турбулентного теплообмена.
Турбулентность называется теплопроводностью. Для сравнения турбулентных (VI1-71) и ламинарных (VII-29 b) уравнений энергии пограничного слоя последнее приведено в виде (VI1-29 c): Если сравнить формулу (VII-7I)с (VI1-29 c), то можно увидеть, что первые 2 члена были добавлены. Первый Турбулентность представляет собой диссипативную функцию, или тепло, возникающее в турбулентном пограничном слое в результате вязкого воздействия. Второй. А^) высоты-с » РА1^ ’ Он представляет собой тепловой поток, вызванный действием турбулентной теплопроводности.
Концепция турбулентных критериев Прандтля представлена в следующем формате (VI1-73) Помнить это. Коэффициент движения турбулентной вязкости; e = — турбулентная теплопроводность. РСР. Результат решения уравнений турбулентного пограничного слоя получен при следующих допущениях: турбулентный пограничный слой Prtb (VI1-73) и число Прандтля в ламинарном коллатеральном слое Pr равно 1.
Термин, который учитывает значения ламинарного потока X и p, опущен, поскольку предполагается, что он равен P C Aa, X Ad. Исходя из сделанных предположений, решение может быть представлено в следующем виде: St = — Cf или St = — Ct. 212 ′ (В VII-74) Полученные результаты согласуются с результатами слоистых слоев (VI1-48 a и VI1-48 b), но значения коэффициентов трения q и C/, включенных в (VI1-48 a и VI1-48 b) и (VI1-74), отличаются от определений.
Выведена формула для определения коэффициента трения (q) турбулентной границы layer. By определение, коэффициент трения (VI1-25). г. _ пуз4.、 Значение Tc можно определить по уравнению (VI1-64), предполагая, что тангенциальное напряжение ламинарного потока непосредственно вне ламинарного подслоя равно тангенциальному напряжению стенки. — АТВ. делать! г = 0 Коэффициент турбулентной вязкости определяется по формуле.
Эта величина была измерена непосредственно и оказалась комплексно зависимой от скорости WX пограничного слоя, что затрудняет ее использование в расчетах. Особое внимание следует обратить на следующие ситуации: несмотря на то, что коэффициент динамической вязкости равен p. турбулентная вязкость А₀ аналогична по форме, но отличается по физическим свойствам. Первое является функцией состояния жидкости, второе зависит от режима движения. Полуэмпирическая теория турбулентности .
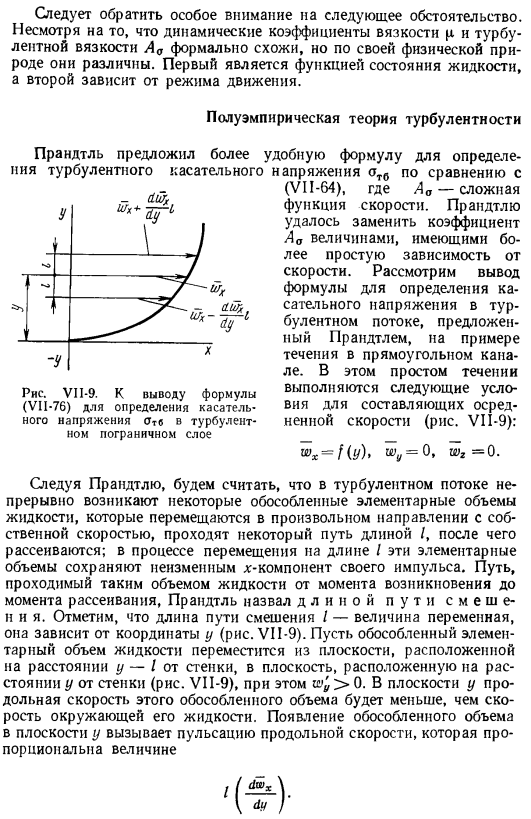
- Прандтль предложил более турбулентный тангенс Рисунок VI1-9.To вывод уравнения (VII-76) для определения напряжения сдвига aTb турбулентного пограничного слоя Удобная формула для определения напряжения сравнивается с (VII-64).Где a-комплексная функция скорости. Прандтлю удалось заменить коэффициент а на величину, имеющую более простую зависимость от speed. As на примере течения в прямоугольном канале рассмотрим вывод уравнения для определения напряжения сдвига турбулентности, предложенного Прандтлем.
Этот простой поток удовлетворяет следующим условиям для составляющих средней скорости (рис. VI1-9): wₓ^ ф(г),^ = 0,^= 0. Предполагается, что в турбулентном потоке, следующем за Прандтлем, непрерывно возникает изолированный элементарный объем жидкости, который движется со своей скоростью в любом направлении, проходит путь длиной l, а затем disperses. In в процессе движения по длине I эти элементарные объемы не изменяют х-компоненту импульса. Путь движения таких объемов жидкости от момента ее возникновения до момента диспергирования назывался длиной расчетного пути и I.
Постулат Кельвина: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара». Людмила Фирмаль
Отметим, что длина пути смешения/является переменной и зависит от координаты y(рис. VI1-9).Перемещение изолированного элементарного объема жидкости от стенки к плоскости на расстоянии y-I, а от стенки к плоскости на расстоянии y(рис. VII-9).^> 0. в плоскости y продольная скорость этого изолированного объема меньше скорости окружающей жидкости. когда в плоскости y появляется другой объем, в вертикальной скорости возникает пульсация.
Это… 、 Разделение жидкостей когда основной объем перемещается из плоскости 4-I в плоскость y (w} 0), его продольная скорость больше скорости окружающей жидкости. если в плоскости y появляется другой объем жидкости, возникает пульсация проольной скорости. Это… 、 Поскольку положительные и отрицательные пульсации скорости происходят с одинаковой вероятностью, абсолютное среднее пульсаций скорости вдоль оси x равно половине суммы рассмотренных 2 пульсаций. абсолютное среднее значение пульсации скорости вдоль оси y 1 ^ 1 = / — ^- (VI1-75) Да. И затем — 7-g, 2 / dwₓ\ 2 №.).
Объединив последнее уравнение и соотношение (VI1-64) [88], получим уравнение, определяющее напряжение сдвига турбулентности. АТБ = — р; (е; = пп. Для условий пограничного слоя I =принимается за число Прандтля Pr для средних значений. Здесь.、 x-универсальный пропорциональный коэффициент, не зависящий от Fe. Определяется экспериментально. х 0,39 −4 0.40; /- Средняя статистическая длина пути смешивания. Форма последнего выражения предложенной Прандтлем формы такова dwₓ Ди. dwdydy Представление (VI1-76) — это наглядное отражение очевидного положения о нем.
Изменение знака производной, выражение знака результата напряжения сдвига (VI1-76) имеет ряд преимуществ перед(VI1-64).Давайте объясним этот факт. Если мы сравним уравнение (VI1-76) с (VI1-64), то найдем уравнение коэффициента турбулентной вязкости. в dwₓ (VI1-77) Величина I является функцией координаты yy, и исследование показывает, что она не зависит от скорости wx. Означает зависимость коэффициента — При скорости m> x АА проявляется только производной.
То есть выражается конкретно и относительно simply. In по формуле (VI1-64) зависимость АО от скорости значительно сложнее, и по сей день она практически неизвестна. В результате пульсирующего движения жидкости осуществляется дополнительная передача как импульса, так и тепла. Представьте тепловой поток, вызванный турбулентной теплопроводностью (VI1-70) в следующем виде — P5yL / = 7tb, (VII-78) Где h ’- cpO ’ — пульсация энтальпии жидкости.
Предполагается, что пульсация энтальпии может быть выражена в среднем значении следующим образом: Где/ t-длина пути перемещения теплового потока. Формула теплового потока (VII-75), принятая во внимание, может быть выражена следующим образом: — ^’=₉ₗG = P / / T ^ — G (VII-79) Формула (VII-79) выводится на основе рассуждений, аналогичных тем, которые использовались при выводе формулы (VI1-76). Уравнения(VII-76) и (VII-79) являются основными соотношениями в полуэмпирической теории турбулентности [A5].
Метод исследования теплообмена с использованием основных соотношений полуэмпирической теории турбулентности рассмотрен в§ 9 настоящей главы. Универсальный закон распределения скоростей Рассмотрим участок вблизи стенки потока в канале с плоской стенкой. Рассматриваемая область стенки включает в себя ламинарный коллатеральный слой и очень мелкий слой турбулентности над ним. Общая толщина этой области значительно меньше расстояния от стенки до оси канала h. In выводя закон распределения скоростей в области вблизи стенки.
Прандтль сделал 2 предположения. 1 — й увеличивается линейно по мере увеличения длины пути смешивания/расстояния от стенки / = ХД /、 Где Х-коэффициент пропорциональности безразмерной постоянной, определяемый по опыту. Во-вторых, напряжение сдвига области стены не изменяется, равное напряжению сдвига стены Учитывая эти предположения, прандулярную формулу (VII-76) можно представить следующим образом: МИП Ч = Р».* Г!2. (VII-763) Здесь плотность жидкости на стене. Значение слева от результирующего выражения называется динамической скоростью стенки, которая обозначается символом и*.
Если разделить переменные с учетом принятой нотации, то это выглядит так: Интеграция и поиск (VI1-80) Поскольку этот метод может закрыть распределение скорости и ламинарное распределение скорости подслоя в турбулентной части области стенки, постоянная C найдена с использованием границы стенки conditions. In другими словами, тангенциальное напряжение ламинарного и турбулентного течения замыкается вблизи верхней границы 1 ламинарного подслоя.
Далее по шлихтингу (88) определим интегральную постоянную c (vi1-80) из условия, что скорость жидкости равна bullet = 0 на некотором расстоянии yQ (1 /величина того же порядка, что и толщина слоистого подслоя) от стенки. С = — ^ 1П Т /₀. (VII-80) заменить значение C на d> x = — ^(1n //-1n//₀). Самонадеянный (Где p-безразмерная константа) и представляет последнее выражение в виде ^Л± ± Я ₍^^Xₗₙ В, Х \ В (В VII-81) Формула (VII-81) представляет собой зависимость безразмерной скорости wjv *от безразмерного расстояния yvjv вдоль y-axis. In в уравнении (VI1-81) константы x и 0 определяются экспериментально при исследовании течения в трубе, поэтому их значения приведены в§ 10 настоящей главы.
В соответствии с указанным Выражение (VI1-81)может быть выражено в виде Ф01)=ЛН+ (VI1-82) Формула (VI1-82) является содержанием универсального закона распределения скоростей, который справедлив как для течения вдоль пластины (течения в канале), так и для течения в круглой трубе. Закон (VI1-82)используется при изучении процессов трения и теплопередачи; он был экспериментально подтвержден на примере захоронения.
Заметим, что уравнение (VI1-82) дает лучшие результаты для течения с большим числом Рейнольдса, где турбулентное напряжение сдвига является доминирующим, поскольку учитывается только турбулентное напряжение сдвига, а ламинарное напряжение не учитывается при выводе закона (VI1-82) турбулентного сдвига области вблизи стенки потока. Для умеренного числа Рейнольдса получен степенной закон распределения скоростей с учетом ламинарного stress. It может быть представлена в следующем виде Ф-01) — СП / Л- (VI1-83) Показатель 1 / .h составляет около 1/7, практически не зависит от числа Рейнольдса. Значение c зависит от стр.
Смотрите также:

