Оглавление:













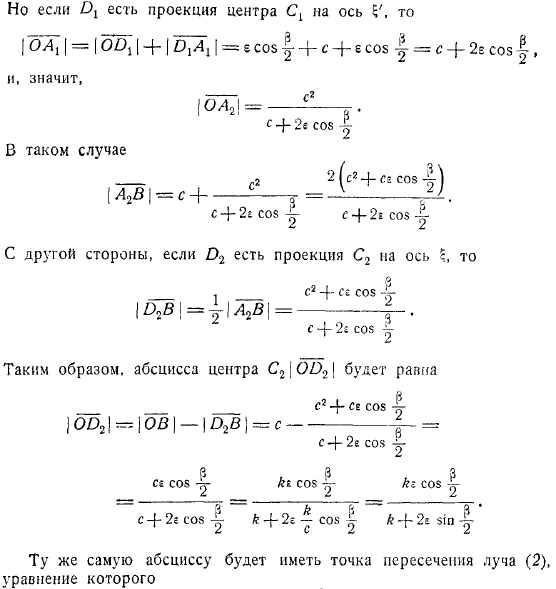
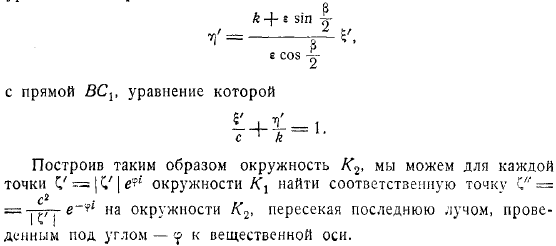


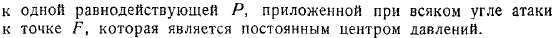

Обтекание профилей Жуковского
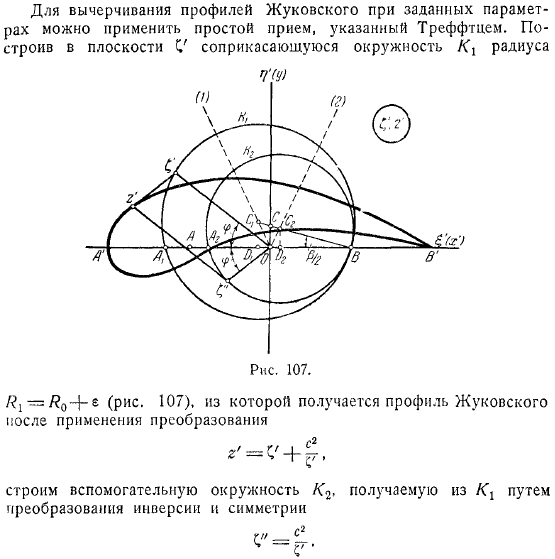
Конформное преобразование гидромеханики, используемое для исследования обтекания эллиптического столба, представляет собой единичный радиус окружности в плоскости отрезка действительной оси между эллипсом и фокальной точкой в плоскости, а соответствующая точка проходит раза в противоположном направлении к этому отрезку при обтекании эллипса. Это отличный способ не отставать от своих друзей и. Форма, ввести новые переменные и, используя аналогичные переменные. Завершите преобразование.
Преобразует окружность из плоскости в радиус в сегмент, который в раза смещен от реальной оси плоскости. Введение в. В этой форме вы можете видеть, что окружность плоскости находится в центре виртуальной оси в нескольких точках, которые проходят через точку и становятся реальной осью. Окружность на плоскости от действительной оси, помещенной в точку, входит в дугу, имеет вершину в точке на мнимой оси, и дуга проходит через раза. На самом деле, точка плоскости соответствует точкам плоскости, а точка пересечения окружности и мнимой оси.
Вы можете видеть, что прямо идете к той же точке на плоскости, кроме. Число модулярно, и аргументы, через. Где комплексные числа, описанные выше, представлены векторами, где углы, под которыми сегменты видны из точки тоже. Для то есть линия профилей цилиндров будет дугой окружности. Поэтому преобразования. Отображает полный круг плоскости, код которого вмешивается с центральной стороны угла, и, следовательно, под центральным углом фигуры. Дуга плоскости хорды, идущая от противоположной стороны к центру, основана на центральном угле.
Радиус дуги можно найти из треугольника. В этом случае полная окружность круга соответствует дуге. На рисунке точка, радиус главной окружности, так что она является касательной к главной окружности. После применения преобразования, потому что круг полностью покрывает круг. Перейти к замкнутой кривой, которая охватывает дугу. Точка, кривая касается дуги и приближается к ней с обеих сторон, то есть образуя точку. Если оси, параллельные оси, прорисованы через центр окружности, то точки комплексной плоскости относительно новой оси соединяются с соответствующими точками плоскости с помощью трансляционного преобразования.
Здесь комплексное число плоскости, представляющей вектор, если ввести его с учетом угла наклона радиуса главной окружности относительно отрицательного направления действительной оси, то получим ось. Извините. Где. Поэтому Л. Здесь окружность окружена поступательным потоком циркулирующего в плоскости, так что скорость этого потока на бесконечности также образует положительное направление и угол действительной оси. Поэтому комплексный потенциал такого потока выражается следующим образом: здесь мы представляем.
- Сначала мы будем использовать основание. Здесь мы проходим через на основе уравнения, дающего, затем. Получаем комплексный потенциал течения при обтекании профиля в плоскости расчет комплексной скорости на бесконечности течения в плоскости. Таким образом, скорость потока в плоскости сзади в петлю я бесконечен, как видно из уравнения комплексная скорость, где. Чтобы сделать задачи об обтекании профилей имеют физический смысл, скорость потока включение и выключение профиля должно быть конечным. Поэтому, выберите прочность.
Остается неопределенным для удовлетворения требований конечности. Для этого достаточно выбрать так, чтобы в точке на плоскости была. Когда вы выполняете расчет, вы увидите, где он находится. Или, чтобы вычислить здесь основной вектор гидродинамических реакций на единицу длины цилиндра, приложенной к профилю стороны потока, воспользуемся формулой Кутты Жуковского. Здесь, подставляя выражение. Вектор, ориентированный перпендикулярно вектору скорости, называется несущей способностью величины. Для малого, вы можете положить его приблизительно. Или за что. Нет.
Подъёмная сила сегмента крыла бесконечного размаха равна произведению плотности газа (жидкости), скорости газа (жидкости), циркуляции скорости потока и длины выделенного отрезка крыла. Людмила Фирмаль
Е. Жуковский будет иметь ту же формулу, применяя преобразование. Она показана Чаплыгиным и не отличается по существу от трансформации. Или применитесь к вышеуказанному. Профиль, полученный путем применения того или иного из указанных преобразований к конкретной окружности, соприкасающейся с основной окружностью в точке сингулярности преобразования и заключающей в себе сингулярность, получает общее название профиля Жуковского, который впервые был использован в качестве профиля крыла самолета.
- Профиль Жуковского на заданном расстоянии в плоскости профиля между сингулярными точками преобразования характеризуется параметрами. Параметр характеризуется изгибом или кривизной крыла, а параметр — толщиной. При небольшом изгибе можно занять практически любое место, где площадь составляет единицу длины крыла, после чего вы получите простую формулу несущей способности. В случае это дает уравнение несущей силы в смешанном потоке с циркуляцией плоской пластины шириной. Однако величина циркуляции выбирается таким образом, чтобы в конце пластины скорость потока оставалась конечной.
Этот результат уже получен по приведенной выше формуле. Указывает, что если угол (также называемый углом атаки) принимает максимальное значение, то несущая способность исчезает, изменяя направление. Плюс-минус. Где происходит так называемый стрелочный прогиб кривой дуги. Формула теоремы Чаплыгина представляет несущую способность потока, когда он обтекает дугу без перерыва. Бесконечная скорость решетки параллельна струнам, которые укорачивают дугу, и не зависит от длины дуги или радиуса конкретного.
To построить профиль Жуковского с определенными параметрами можно применив простую технику, которую Треффт. На плоскости построен радиус контактной окружности. Рисунок, профиль Жуковского, полученный после применения преобразования, построить вспомогательную окружность, полученную из путем преобразования инверсии и симметрии. Это преобразование, круг становится кругом, реальная ось становится самой собой, а круг благодаря своей пригодности (он пересекает реальную ось под тем же углом, что и круг).
Другими словами, соприкасаются друг с другом в точке, через которую они проходят. Итак, центр окружности, прямая линия. С другой стороны, центр находится не в точке, соответствующей центру окружности, а на луче, который является отражением лучей от воображаемого. Дело в том, что точки пересечения окружности с фактической осью соответствуют, поэтому выглядит это так:но если есть проекция центра на ось, то, следовательно. В этом случае при использовании, если имеется проекция на ось, при использовании абсцисса центра равна.
Та же абсцисса есть точка пересечения лучей уравнения, которая является линии, уравнение которой пересекает конец с лучом, проведенным под углом к оси материала. Создав геометрическую сумму вектора и, получим соответствующую точку профиля Жуковского. Используя полученные результаты, можно составить полное описание гидродинамических реактивных сил, приложенных к профилю Жуковского при. В нашем случае конформное преобразование плоскости в плоскость выглядит как равенство. Получить.
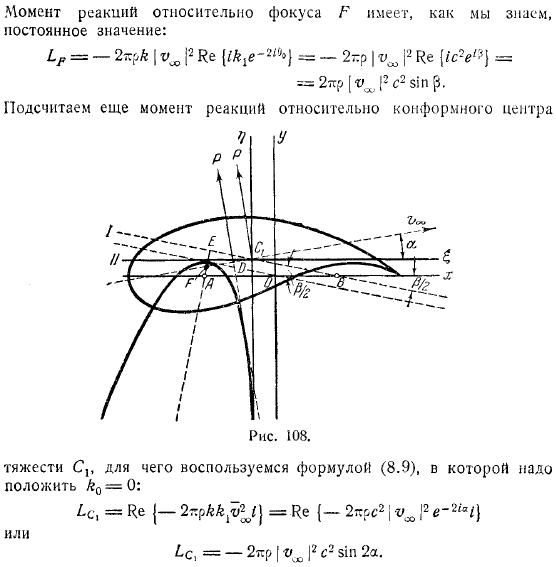
Случай острых кромок профиля Жуковского, а следовательно, конформный центроид профиля четко координирует. Имеет. Это соответствует точке. Фигура. Фокус профиля определяется по формуле. Это указывает на то, что направление симметрично с направлением критической оси на ось, а расстояние между точками определяется по формуле. Зная, что стабильная парабола и фокус ее директора являются критической осью профиля, вы можете легко настроить эту параболу. Параметр o имеет значение. Момент реакции на фокус имеет, как известно, постоянную величину.
Также вычисляет момент реакции для конформного центроида с помощью. Понятно, что этот момент исчезнет в. Таким образом, если бесконечно большой поток параллелен оси Ox или Oy, то сила реакции проходит через точку, поскольку она ориентирована вдоль оси, параболической устойчивости, как непосредственно, так и непосредственно.
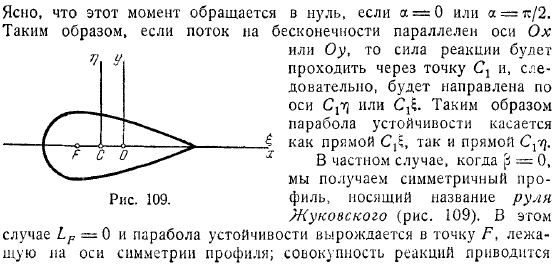
И в некоторых случая вы получаете симметричное пространство. Фил, названный рулевым Жуковского Райсом. В этом случае парабола устойчивости вырождается в точку на оси симметрии профиля, а набор реакций сводится к результату самонастройки, который прикладывается под произвольным углом атаки к точке, являющейся постоянным центром давления.
Направление действия подъёмной силы получается поворотом вектора скорости набегающего потока на прямой угол против циркуляции. Людмила Фирмаль

