Изгиб кривого бруса не в плоскости его начальной кривизны

Изгиб кривого бруса не в плоскости его начальной кривизны

Изгиб криволинейных балок не в плоскости начальной кривизны Выше мы впервые подняли вопрос об изгибе криволинейного стержня в плоскости кривизны. Однако сила, действующая на кривую балки, не может находиться в плоскости оси балки!). в таких случаях необходимо учитывать изгиб балки и скручивание балки в 2-х вертикальных плоскостях.

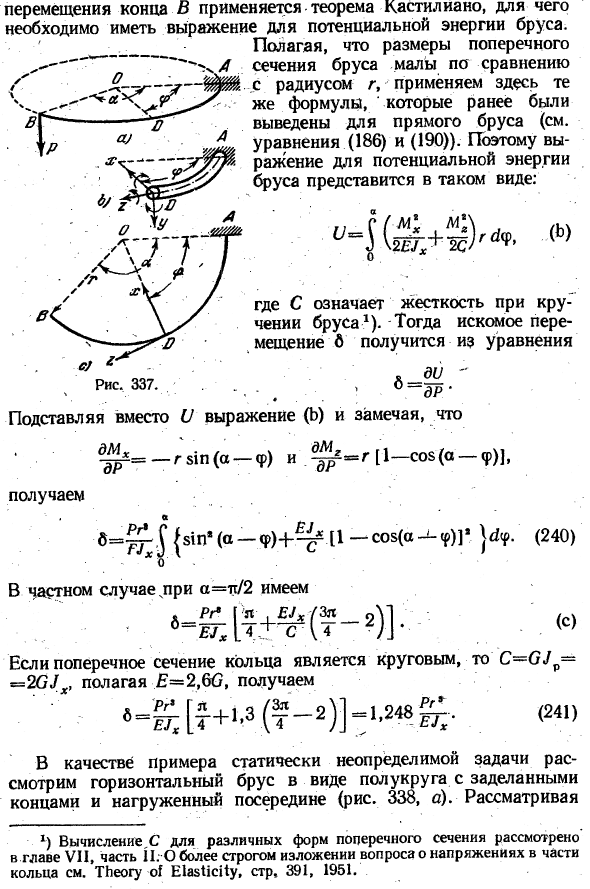
• Простая задача такого рода показана на рисунке. 337, а, часть горизонтального кругового кольца, встроенного в секции А, В2) нагружена вертикальной нагрузкой Р, приложенной к концам.337, В и 337, с), принимая во внимание поперечное сечение балки О и принимая оси, момент внешней силы Р К этим осям имеет следующий вид: — Pr8ip(а-<р), му = 0、 ҐLg-ПР | 1-соз(а-ЛП)]. (ля）

Предполагая, что размеры поперечного сечения балки малы по сравнению с радиусом/, здесь мы применяем ту же формулу, ранее выведенную для прямой балки(см. уравнения(186)и (190)).Поэтому формула для потенциальной энергии пучка представлена в виде: В. * (К 5 \ 2UX 12Ç. jrdy,..(си） Где c-бар) 1).

Используя эти формулы, можно рассчитать напряжения от изгиба и кручения в любом поперечном сечении. При вычислении смещения конца B теорема Кастильяно имеет вид applied. To для этого нам нужна формула, представляющая потенциальную энергию луча. Людмила Фирмаль

Тогда искомое смещение b получается из уравнения 。 ди. » ;- доктор’ Подставим выражение (Б), но будьте осторожны с ним G8sh(о — <р)и^ = Р [1-«»(А — <Р）]、 Мы получаем (а-> р) н-> 11-А(А — * — (Ф>)] Е) ды. (240） I{3、»- л РГ.＃ с == ТТА В некоторых случаях при a =η/ 2 (С） Если поперечное сечение кольца круглое, C = GJV — = 2£ / x, установите£ = 2.6 (7、 b = [t + 1-3(t-2）] = 1> 248 ^、（241）

В качестве примера статически неопределенной задачи рассмотрим полукруглую горизонтальную балку с заложенными обоими концами и Центральной нагрузкой(рис. 338, а).Рассматриваемый * ) Расчет. Различные формы поперечного сечения C описаны в Главе VII, Часть II. теория упругости, pp для более строгого представления задач о напряжениях на кольцевой части. Посмотреть 391, 1951.

Только небольшое вертикальное движение луча, движение в горизонтальной плоскости, может быть полностью проигнорировано как небольшое количество более высокого order. As а в результате кольцо не сгибается? Принимая во внимание силы или моменты этой плоскости на ее плоскостях, концах A и D, замкнутых концах, приходим к выводу, что из состояния равновесия там действует вертикальная реакция P / 2, а момент Mx = Pr12.

• Момент MXo также работает, предотвращая вращение конца B относительно оси r0.Величина этого момента не может быть определена из уравнения статики. Найдите его, используя минимальную рабочую теорему. ^ = 0. (си） немецкая марка. Иди.

При выводе уравнения потенциальной энергии пучка обозначим момент, приложенный к краю B векторами Pr/ 2 и / U * 0, как показано на Рис.5. 338, б. — момент Mx и Mx на сечении O будет равен: * РГ. Rg. МХ =-^ с05 <Р-Mxo в CXF-uBtf. (ми)） (0 $ 1Н Ф4 MXo ЭПР Ф — … (1-КНИ Ф）、 Выражение потенциальной энергии показано в следующем виде: • — М, М’х М’л У = 2) \ WX с + 1С)р ^ — (г） 0. Подставим эту формулу в Формулу (b)、 дмж употр ’ употр АЛГ = с°5 Ф、 — БШФ.、 Иди!

Мы получаем Откуда. (£- я)=-0.I82 / > r (242） Знак минус указывает, что направление МГП противоположно направлению, показанному на рис.338, А. из уравнений(е)и(0) можно получить изгибающий момент и момент кручения любого поперечного сечения.

Максимальное отклонение явно находится под нагрузкой, поэтому его можно легко получить из Формулы Кастильяно. л Ди / м 6 = д-р*(б） § Замените выражение на И И обратите на него внимание ^ = г (СС * Ф-БИПП）、 (Я） употр др » Мы получаем (виги Ф ^ -ГП Ф 1）、 6 = m — x {(2 — °-363) (m-m)+ + С * [(2 −0.363)(х + Т)+ Т-4 + 0.363 ^ = 0.514 ^.

При нахождении частной производной (1) мы проигнорировали тот факт, что крутящий момент < Mg>не является независимой величиной, а представляет собой функцию P, которая определена в Формуле (242). Людмила Фирмаль

Если принять это во внимание, то правая часть формулы (b)записывается следующим образом: Диди. ДР+ДЩ,■ИГ М Однако, согласно уравнению (b), 2-й член этого уравнения исчез.

Поэтому предыдущий метод определения прогиба d является обоснованным. Возможно, вам придется рассмотреть кривые для баров, где ось не является плоской кривой, и в этом случае у вас будет пространственная проблема. Проблемы такого рода возникают, например, при расчете ребер жесткости трубчатого фюзеляжа. 1)статья К. см. Marguerre, авиации. Форш, Т. 18, 253-61 страницах 1941 года.

Натуральный. Консультативный. Воздухоплаватель хм, мэм, Н 1005.1942, Н. см. также Джей Хофф, цитаты, стр. 330. Задачи 1.На ось вращения и криволинейную балку a = l / 2 (рис.337) на конце нагружена витая пара Mg => T. Найдите вертикальное перемещение ребра B. Тгг.

Ответ. если предположить, что £ / x / C = 1.3, то a = 0.506 p-y. 2.Мы решаем предыдущую задачу, предполагая, что пара изгибов MX = * M0 приложена к краю B на вертикальной плоскости, которая является касательной к оси точки B. Ответ. а = 1,150.

Балка в виде полукруга с осью в горизонтальной плоскости герметизирована сечением а и и и симметрично нагружена двумя вертикальными нагрузками Р в сечении С и>>(рис. 339). Ответ. МГО—^ — пр-сое П-строку P ^. 4.To решается предыдущая задача в случае равномерной вертикальной несущей способности, распределенной по всей длине балки. Ответ. Мг $ = — <7Г2^ =-0.32?Р2. а. полукруглая горизонтальная балка, показанная на рисунке, как и в предыдущем выпуске, равномерно нагружена на 339 и находится на средней площади поперечного сечения R. найти вертикальную реакцию N опоры£. Ответ. Н-вz2qr.

Смотрите также:

Предмет сопротивление материалов: сопромат 

Момент инерции плоской фигуры относительно оси, лежащей ее плоскости	Уравнение изогнутой оси для бруса с круговой осью
Полярный момент инерции плоской фигуры	Изгиб кривых труб