Оглавление:






Изгиб кривых труб
Трубогибочный При выводе закона распределения напряжений вследствие изгиба криволинейного стержня (§ 77) предполагалось, что профиль поперечного сечения не изменяется. Поскольку очень малые смещения в плоскости поперечного сечения вследствие бокового сжатия или расширения существенно не влияют на распределение напряжений, это предположение справедливо до тех пор, пока существуют сплошные стержни.
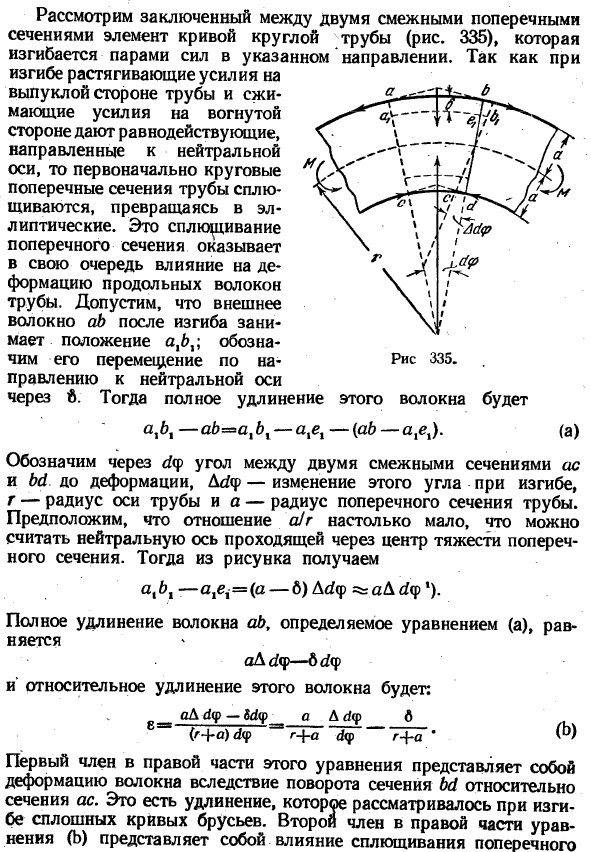
- Однако при изгибе тонкой изогнутой трубы условия меняются completely. It известно, что криволинейные трубы с относительно тонкими стенками имеют меньшую изгибную жесткость, чем это прогнозируется согласно обычной теории криволинейных стержней2).Поэтому в таких случаях необходимо учитывать искажение поперечного сечения при изгибе 3). Рассмотрим криволинейный элемент круглой трубы, ограниченный двумя смежными участками (рис.335).
Этот изогнутый элемент изгибается парой сил в указанном направлении. Во время гнуть, выпуклая сторона трубы но сила напряжения и вогнутая сторона сжимающая сила производят результат направленный к нейтральной оси, так, что первое круговое поперечное сечение трубы будет сплющено и повернет в Oval.
В свою очередь, уплощение этого поперечного сечения влияет на деформацию продольных волокон трубы. Предположим, что внешнее волокно ab занимает положение axbx после изгиба; указывает на движение в сторону нейтральной оси И идеальное расширение этого волокна ах-ах = * ах-АХЕ-(АБ-АХЕ). (ля) Угол между двумя соседними секциями обозначается<π. W перед деформацией, D * yr-изменение этого угла при изгибе, g-радиус оси трубы, а a-радиус поперечного сечения трубы. Соотношение а!
Предположим, что R очень мало, поэтому можно рассмотреть нейтральную ось, проходящую через центр тяжести поперечного сечения. Людмила Фирмаль
Далее, с фиг. axbx-ахх =(А-B) Дир = ^ ад ’). Общее удлинение волокон, определяемое формулой (а), составляет объявление ^ Ф — б ^ ф И растяжение этого волокна выглядит так: ОА Ар-му а а Ар б、 8 = (г + а)(1 <р а г-\ — в ар н.«» Первым членом в правой части этого уравнения является деформация волокон при вращении секции bb в секцию ac.
Это относительное удлинение учитывается при изгибе сплошного криволинейного бруса.2-й член в правой части уравнения (b) — это эффект уплощения поперечного сечения. Очевидно, что это влияние очень важно. Например, r + — a = 150 сук, 6 = 0,05 см. Значение — ^ — = 1/3000 и соответствующее напряжение р п в Стальная труба^ — ^ — = 2, L0e −1 / 3000 = 700 кг! она будет равна см2. В результате очень небольшое уплощение поперечного сечения значительно снижает напряжение крайнего волокна ab.
Аналогичные выводы можно сделать и о волокне L, которое расположено на вогнутой стороне трубы. Изменение направления изгибающего момента сопровождается изменением знака нормали stress. As в результате вместо уплощения трубы в радиальном направлении происходит уплощение в направлении, перпендикулярном плоскости чертежа.
Тот же вывод, что и выше, может также указывать на то, что уплощение поперечного сечения вызывает уменьшение напряжения самых дальних волокон. Таким образом, можно сделать вывод, что волокна трубы, наиболее удаленные от нейтральной оси, не участвуют в распределении напряжений, которое обычно предписывается в теории изгиба.
- Это влияет на изгиб трубы точно так же, как и уменьшение момента инерции. Поэтому вместо формулы, выведенной для непрерывной кривой стержня (214), при определении деформации узкой кривой трубы следует использовать следующую формулу: l ^ = 4-й> — (236> Здесь£ — числовой коэффициент, меньший единицы, который учитывает эффект сплющивания. Этот коэффициент зависит от размера трубы и может быть рассчитан по следующей приближенной формуле): £= 1- (237) 10 + 12. (*) »
Где T-толщина стенки трубы. Эта формула показывает, что эффект уплощения зависит только от величины отношения tria2. Что касается влияния уплощения на распределение напряжений, то Калман вместо обычного уравнения нормального напряжения при изгибе (o2), (/означает расстояние ’) См. статью й. Kàg inâp * a, P. цитата в 340.а) r велик по сравнению со сном, и гипотеза линейного распределения напряжений считается достаточно точной.
От нейтральной оси вам нужно использовать следующую более сложную формулу (с) Куда? β=- Максимальное напряжение, определенное по формуле (ам), равно ^、-■•§ 7″(238) Я’% Где th-наружный диаметр трубы. Два Черт возьми! Ущелье 3К — Коэффициент рассчитывается в зависимости от размера трубы; в следующей таблице 15 приведены некоторые значения/ л. x * таблица 15 Значение^в выражении(238) т. тр около 0.3 0.5 1.0 * 1 1.98•1.30 0.88
Это показывает, что если отношение/ g / a2 мало, то фактическое максимальное напряжение намного выше напряжения, определенного на основе обычной теории, и эффектом уплощения поперечного сечения пренебрегают, для потери M прямоугольного сечения мы также можем сделать вывод, аналогичный предыдущему. Людмила Фирмаль
Например, если поперечное сечение представляет собой узкую трубку квадратной формы, то мы видим, что коэффициент k в Формуле (236) зависит от соотношения. б. * /- Толщина стенки трубы, g-радиус оси трубы, b-длина стороны квадрата, определяемая по следующей формуле:- Вы. *. л ^ −0.0656 п• x) такие проблемы возникают, например, при проектировании кранов Feir-Beirn. Сноска 3, стр. 340. Например, если rr= 0.1 и// / / = 50, то= = 25 и = = 0.63.Максимальное напряжение трубы с прямоугольным поперечным сечением возрастает обратно пропорционально жесткости.
То есть в приведенном выше примере искажение поперечного сечения увеличивает максимальное напряжение примерно на 60% 1). Если поперечное сечение изогнутой балки имеет полки значительной ширины, то вопрос об искажении поперечного сечения снова будет иметь практическое значение. Например, задача заключается в исследовании изгибных напряжений m в узлах жесткой рамы с двутавровым сечением (рис. 336).
Если мы посмотрим на элементы каркаса, ограниченные смежными 2-мя поперечными сечениями Mn и mn19, то увидим, что продольное напряжение от изгиба полки имеет радиальную составляющую, которая стремится к изгибу полки (рис.336, б). в результате этого изгиба происходит незначительное уменьшение продольного направления рис. 336.Напряжение * от изгиба o некоторых полок、
Он расположен на значительном расстоянии от walls. To учитывая эту ситуацию, эффективная ширина полки ob должна использоваться вместо секции I, а не фактической ширины ширины полки. Р-1.32 ^, (С) / — Толщина полки, r-радиус кривизны полки. Для внутренней полки r = * r», для внешней полки r = gL. Расчеты показывают, что при р <0,65 изгиб полок незначителен и теория, описанная в§ 79, может быть применена непосредственно.
Если значение P велико, вы можете использовать уравнение 2) для расчета продвижения полки А6 =(- п-б.(е)) 1) L для дальнейшего развития теории изгиба изогнутой трубы. См. Бескин. Пмтф. Механик. Т. 12. 1945, Е. Р апэг ы, тр, Нат. Акад. СИЭ., Т, 35, стр. 204, 1949; Р. А. С 1 А Г К, Т. 1. Г я 1 пойду и Е. Р Е П Е Д. Дж. Заявл. Механик., Т. 19, 1952.- * ) Для заключения этой формулы обратитесь к докторской диссертации Otto S t e i n h a d d t * a, Dal Stadt. 1938 год. Результаты экспериментов, проведенных S t e i p h ad o m, хорошо согласуются с формулой. Например, если полка имеет ширину 6 = 15 см, соответствующий радиус равен r = 20 см, а толщина f = 2,5 см, то формула (b) составляет p = 2,80, а эффективная ширина полки равна 0,35*. 15 = 5,25 см.
Смотрите также:
Предмет сопротивление материалов: сопромат

