Оглавление:




Уравнение изогнутой оси для бруса с круговой осью
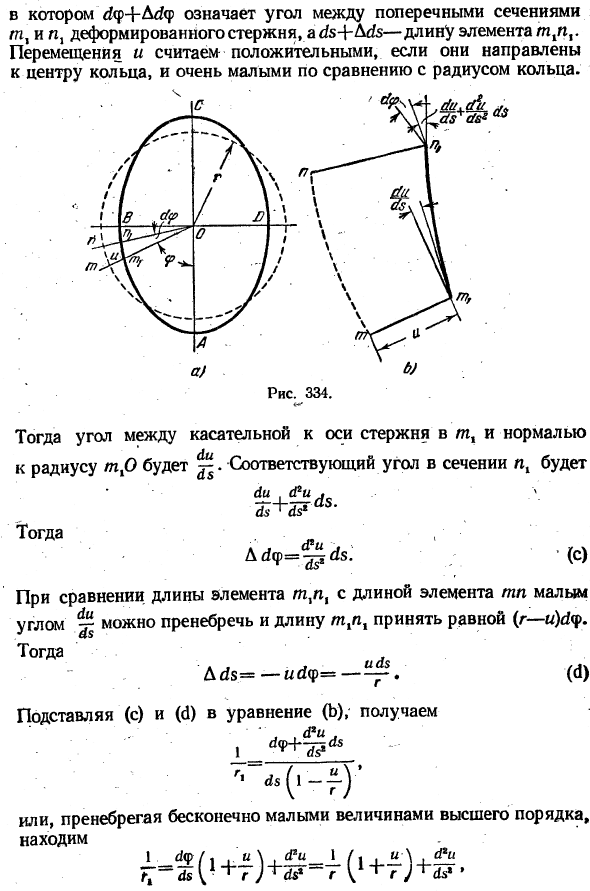
Для тонкой изогнутой балки с круговой осью дифференциальное уравнение для изогнутой оси аналогично уравнению для прямой балки (уравнение (79)стр. 124). Сделайте так, чтобы АБКО (рис.334) представляла собой ось кругового кольца после деформации, что означает небольшое радиальное смещение отдельных точек этой оси.
- Изменение кривизны оси стержня при изгибе может быть исследовано с учетом элемента mn кольца вследствие деформации и соответствующего элемента ямы деформированного кольца между одинаковыми радиусами (рис.334, б).
Начальная длина элемента tp и его начальная кривизна выглядят следующим образом. Людмила Фирмаль
При малых деформациях кривизна одного и того же элемента после деформации равна кривизне элемента mx%.Последнее определяется уравнением с / ф + A4f (Си) 77 _І55-І — ^ ^ 5• Где^φ+ A ^φ означает угол между сечением m и n деформированного стержня, а (k + M& — означает длину элемента m1n.
Если смещение направлено к центру кольца и очень мало по сравнению с радиусом кольца, то смещение считается положительным. В этом случае тангенс оси стержня в единицах mx и радиус tn. угол между нормалями fi равен^.Соответствующие углы сечения px являются С трех АР + г *- Затем. ( (с)
- При сравнении длины элемента mnn и длины элемента mn малый угол пренебрежимо мал, а длина mnn равна (r-u)c! Может быть равно < N>. си® И затем… &с15 = —и(1У =-.(ы!) подставляя © и (c1) в Формулу(b), получаем: Карманные кражи 1 **!& «гн» — ту Или если мы игнорируем бесконечно малые высшего порядка、 1- ^ 2(1 + ^ 4 ——(1 л.-)*- Откуда? 1.1 и < Ri-h р, р ^
Зависимость между приращением кривизны тонкого стержня на основе формулы (214) и величиной изгибающего момента выражается следующим образом: Р | •р ЭЖ. В.) Знак минус справа от этого выражения зависит от знака изгибающего момента.
Изгибающий момент считается положительным, если он уменьшает начальную кривизну стержня(рис. 308). Людмила Фирмаль
Уравнение, (e)и(0 к、 £ + * — <235> Это дифференциальное уравнение изогнутой оси тонкого Стержень с осью вращения. Для бесконечно больших р это Она совпадает с уравнением (79)прямой балки. В качестве примера применения уравнения (235) рассмотрим задачу, показанную на Рис.2. 320.Равенство (S), p. изгибающий момент tnh%любого сечения на 320 выглядит следующим образом: М = Г(sOZf-
Выражение (235)отображается в следующем виде: (Пу, И ПР (2 а А&+ ^ «» 517 (я С05 фу Или д * у, пр * Ф 2 \ Д ^ + Ш == 2£7У-Косинус(Пи- Общее решение этого уравнения является: пр J в РГ» И потому, что рН-1-Б грех рН + — ^—п-грех рН. Константы интегрирования A и B определяются из условия симметрии.’:\ дю л р \ у. для φ= 0 и
Для φ= 0 и φ=π получим следующее: (^) φ= о — £г(^)> ПГ / 1 я («И^ Етчя-Т) Эти результаты идеально соответствуют уравнениям (227) и (226), полученным ранее с использованием теоремы Кастильяно*).
Смотрите также:
Предмет сопротивление материалов: сопромат
| Изгиб кривых труб | Двухшарнирная арка |
| Изгиб кривого бруса не в плоскости его начальной кривизны | Напряжения в ободе махового колеса |

