Оглавление:




Напряжения в ободе махового колеса
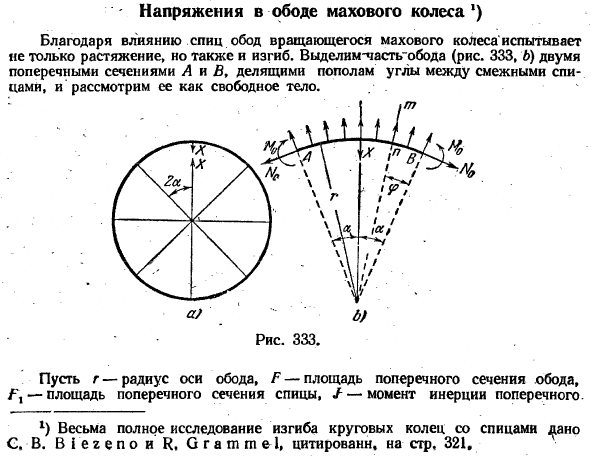
Напряжение маховика Благодаря влиянию спиц, ободья вращающегося маховика будут вызывать не только натяжение, но и изгиб. Различают часпот (рис. 333, б) с 2 поперечными сечениями А и в, углом между соседними спицами пополам и рассматривают его как свободное тело. »
Рисунок 333. пусть r-радиус оси обода, G-площадь поперечного сечения обода, площадь поперечного сечения спиц и момент инерции поперечного сечения. 1) Очень полное исследование по изгибу круглых колец вязальными спицами^ ano C. B. Biezenoh R, Grammel, цитата на стр. 321. — Масса единицы длины спиц, угловая скорость со-маховика.
Из условия симметрии можно сделать вывод, что касательное напряжение не может быть приложено к участку а и участку В, и силы, действующие на эти участки, добавляются к продольной силе и изгибающему моменту M0. Людмила Фирмаль
Если X обозначает силу растягивания спиц, то уравнение равновесия для части обода AB будет иметь вид: 2N0 грех-форекс-2р * — со * грех = 0、 Откуда? Н9—Западная Вирджиния * — фр.— ..(ля) * г 2 грех ’ Любое сечение TP вертикальная сила N N-N. cnsi *(b) г 2 г 2 грех Изгибающий момент того же поперечного сечения Л * р = Л40-Л>(1 —scoscp) 42 греха * ^ Lsin * А.(С) Хотя сила X и момент M0 не могут быть определены из уравнения статики.
- Вы можете найти его, используя минимальную рабочую теорему. Потенциальная энергия Деформация выбранной части АВ-обода отображается в следующем виде*): 0 г г * г г н ЦКР * р д <р、 г> = 2) — Щ-+ 2)Вт — (д> О, Би. LG натяжение в любом сечении спиц на расстоянии р от центра Колесо равно 2 / В= Х + 2 ^(р * — р»). В результате, энергия деформации спиц (ми)) E J2Г,£*о Уравнение, определяющее M0 и X, представлено в следующем виде: 。 JgWn + у + УО,(я) ^(Г,+ (/.)= 0. (г) 1) толщина обода мала по сравнению с g, предполагается, что учитывается только энергия изгиба и натяжения.
Длина спиц считается равной r, но на самом деле она несколько короче R. Из уравнений (f) и (g) подставим их после подстановки (d) и (e Эй. * 1 (1 1 Один. (233) (234) x_ не 2qioY* 0 Фр * Ф * Куда? •,. 。 1 / Син 2а. \ />(а)= 2В ^ [- Γ + −2) ’ т. к. 1• / грех на 2А \ 1 м(о) −2 sints а ^ −4 ^-2) 2а В следующей таблице 14 приведены значения функций f, (a) и ft (a) для различных чисел вязальных спиц N.
Значение функции для выражения таблицы 14 (234) n-4 6 8 Л(а)0.643 0.957 1.274 Ж)0.00608 ′ 0.00169 0.00076 -/ Используя эту таблицу, можно легко определить натяжение спицы X по формуле (234), а изгибающий момент A40 по формуле (233).
После этого продольную силу и изгибающий момент любого сечения RN обода можно определить по формулам (a), (b) и ©). В качестве примера возьмем стальной маховик с радиусом r = 1,5 м, с ободом квадратного сечения 30×30 см2, с 6 спицами поперечного сечения, сечением= 150 СМГ, с частотой вращения 600 оборотов в минуту.
Обод считается свободно вращающимся кольцом. Людмила Фирмаль
Растягивающее напряжение, возникающее в результате действия центробежной силы, равно (см. уравнение (15)) 0.0078. 981. А0 = — о) р * = в −62,8 М 50 * = 705,5 кг1см \ С 6 спицами вы можете сказать: «= 30°,/, (a)= 0.957,(a)= 0.00169.
Следовательно, усилия Согласно формуле (234), можно работать с каждой спицей、 2 ^ω* — С-г.〜300-0.00169 + 0.957 + 6 =1 Согласно формуле (а), продольная сила сечения, делящая угол между спицами на 2, выглядит следующим образом: * 0 =£^ _ 0.0893 ^ = 0.911 ^。 8 8 8 Изгибающий момент того же сечения по формуле (233) выглядит так: yM0 = — 0.605-г-кг см. е.
Самый большой стресс в этом разделе Н М = V-^-°= 644 + 85 = 729 кг / см *. Но… Я посмотрю, что можно сделать. Для поперечного сечения обода, взятого вдоль оси спиц, формулы (b) и © имеют вид < ЛГ)?= «=0.923 ^. (М)^=\, \ ЧД- ^ кгцм. БК. Самый большой стресс в этом разделе Атака= 652 + 167 = 819 кг [см *. В этом случае вы можете видеть, что изгиб обода оказывает лишь небольшое влияние на максимальную величину напряжения, и вычисление напряжения обода, как если бы это было свободно вращающееся кольцо, дает удовлетворительные результаты.
Смотрите также:
Предмет сопротивление материалов: сопромат
| Уравнение изогнутой оси для бруса с круговой осью | Деформация кривых брусьев |
| Изгиб кривых труб | Двухшарнирная арка |

