Двухшарнирная арка

Оглавление:

Двухшарнирная арка

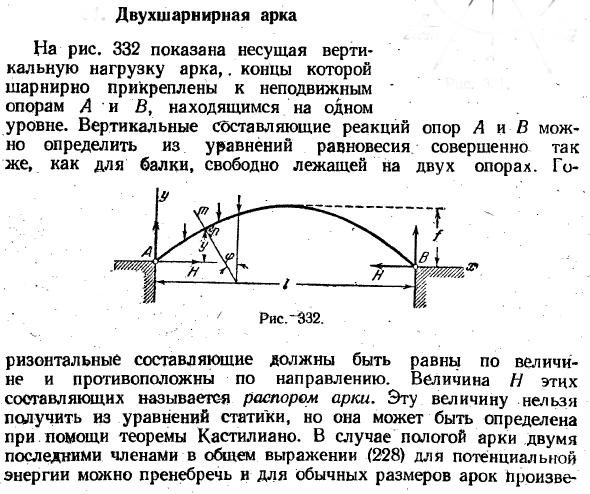
Двойная шарнирная арка На рисунке 332 показана вертикальная несущая арка. Оба конца зафиксированы «поддержкой A» и B прикреплены с осью、 Уровни. Вертикальную составляющую реакции опор а и в можно определить из уравнения равновесия-точно так же, как и в случае балки, свободно лежащей на 2 опорах. Th.- lt. Рисунок-332.

Горизонтальная составляющая должна быть одинаковой по размеру и противоположной по направлению. И размер этих компонентов называется упорной аркой. Это значение не может быть получено из уравнения в статике, но оно может быть определено с помощью Кастильяно theorem.

В случае пологого свода последние 2 члена общей формулы (228) потенциальной энергии пренебрежимо малы для дуг нормального размера, и произведение Fer может быть заменено моментом инерции поперечного сечения Jz. In в этом случае выражение для определения и будет: ду Д Г /. Мг, Ч*. Л, в ДФИ дх J в(2£УФ 1 2 / я).В

Изгибающий момент любой части арки равен М = М0-ч(Ф (б） Где M0-изгибающий момент соответствующего сечения Тот же пролет, что и арка, и мягко лежащие балки с той же нагрузкой.2-й член под интегральным символом Формулы (а)представляет потенциальную энергию продольной силы N и имеет второстепенное значение.

Для свободной дуги с достаточной точностью можно предположить, что эта сила N равна тяге N. Людмила Фирмаль

При назначении формулы (b)и N = H к формуле (a)、 _Ç(М0-.Джимми)ydsÇHds_n Джей Джей, у> О, да. Откуда? ÇM ДС ДС Джей Джей、 — , (229） ’, СРС J EJ,+ J FE 0 0 Для постоянного сечения дуг с обозначением i2 = JF формула (229) может быть представлена в следующем виде: с. ’-. 。 *(230） Ж. ^ ДС-Ф / * J в ДС о’о’о’•• 2-й член в знаменателе представляет собой эффект укорочения оси дуги за счет продольного сжатия.

Часто он невелик и может быть оставлен без внимания. И затем… с. Джей mcyds Ч = — з. (23!） Дж г ДС » Например, параболическая арка, которая использует ось, определенную уравнением, для поддержки постоянной нагрузки, равномерно распределенной вдоль пролета с） И затем… L10 = 4 X(1-X). (д） подставляя © и (b)в Формулу (231), получаем、 Х.- (ми)） 8. / * Фактическая распорка H меньше той, что определена из Формулы (e). чтобы проиллюстрировать идею возможной ошибки A//, соотношение lN приведено в таблице 13 ниже X) для различных арок.

Когда рассчитать количество для включения В этой таблице полное выражение (228) было применено к потенциальной энергии, которая была применена к любому участку арки. EJ0ÇOSÇ ’ И затем Потому что Ф Где/% и EJ0-площадь поперечного сечения и изгибная жесткость арочного сечения ключа, угол φ-угол между поперечным сечением и осью y, а Л-высота арочного сечения.

Формула (E) была применена для расчета количества вход, содержащегося в соотношении^. Таблица 13 Q и» — Коэффициент RR свода / / i 12 1 8. 1 4 ч. 1•1 1 1 1 1 1 1 1 1 л. 10-20- 30 10 20 30 10 20 30- А / А 7 0.1771 0.0513 0.0235 0.0837 0.0224 0.0101 0.0175 0.00444 0.00198 Из таблицы видно, что погрешность, обусловленная применением уравнения (е), существенна только для скромного свода значительной толщины. » A / ссылка на работу автора » Calcul des arcsélastiques*, Paris, ed. Belanger, 1922.

Чтобы вычислить расстояние от изменения температуры, предположим, что 1 опора является подвижной. Людмила Фирмаль

Затем, при тепловом расширении, пролет арки увеличивается на величину alt. Где а — коэффициент линейного расширения материала свода. Распор предотвращает такое расширение свода и может быть найден из условия уменьшения пролета на величину, равную альт. Используя теорему Кастильяно、 дю dÇ(мг./ В * .- , И / Л dH-dH)\ 2EJZ + 2FE)»’! ’ О Если рассмотреть только влияние температуры, а также установить M0-O и N-H, то получим из Формулы (f). 。О, да. Более подробное изучение усилий арки можно найти в книге по теории строительства.

Напряжения в ободе махового колеса	Частные случаи изгиба кривых брусьев
Уравнение изогнутой оси для бруса с круговой осью	Деформация кривых брусьев