Деформация кривых брусьев

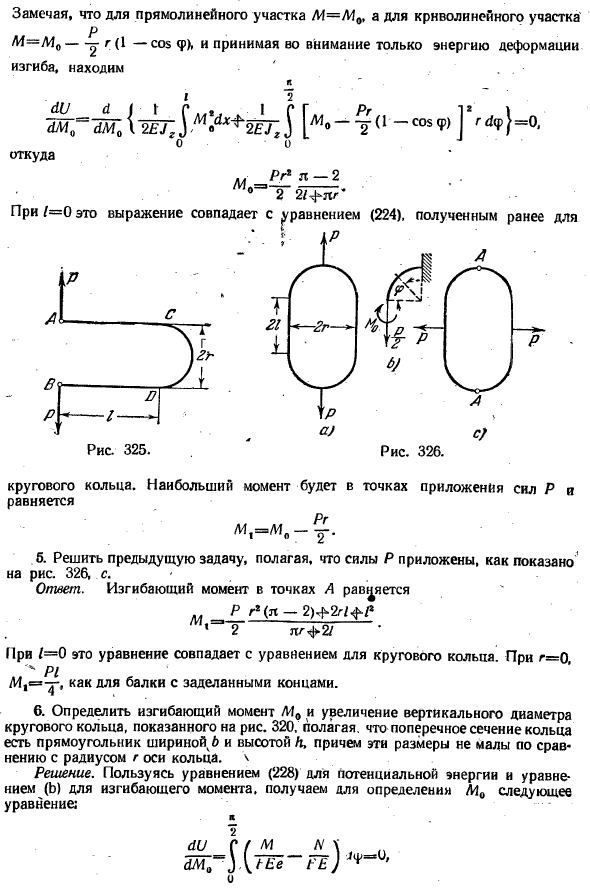
Деформация кривых брусьев

Деформация криволинейных стержней Деформация стержня кривой обычно определяется с помощью теоремы Кастильяно*).Если размеры поперечного сечения балки малы по сравнению с радиусом кривизны ее оси, то начнем с простейшего случая 2).в этом случае изменение угла между 2 соседними сечениями определяется по формуле (214), как и в формуле (А), Р прямой балки.123, энергия деформации изгиба является формулой 5.

• Интеграл охватывает всю длину s балки. Формула (223) аналогична уравнению (1) линейного стержня и смещения точки приложения силы P в направлении P (190). Сила равна 6 = др- В качестве примера возьмем криволинейную балку определенного сечения. Его ось представляет собой 4 минуты 1 дуги окружности.

Кроме того, эта балка нижнего конца а с вертикальным касательным уплотнена, а на другом конце она нагружена перпендикуляром Си. Слева P. изгибающий момент поперечного сечения mn равен M = — iVcos 1С»л ДМ.- 1nn * s » líл* * = ZpJШ7=ЩМ1РгаЧ =oscosvd = плата Z77 с COS <р(л-грех, если)д <р= -. *)

В случае тонких изогнутых стержней потенциальная энергия от вертикальных и горизонтальных сил пренебрежимо мала. См. стр. 322. Худая Лоретта. В качестве второго примера рассмотрим случай тонкого круглого кольца, натянутого с 2 равными противодействующими силами Р, приложенными на обоих концах вертикального диаметра (рис.320).

Из-за симметрии можно рассмотреть следующее Х. Людмила Фирмаль

Сделан вывод, что квадрант равен только 1 (рис.320, Б), а сечение mn не имеет касательной силы, действует только растягивающая сила, равная P / 2 и изгибающий момент M0.Величина этого момента не может быть определена статически и может быть найдена с помощью теоремы Кастильяно.

Из условия симметрии можно сделать вывод, что поперечное сечение mn не вращается даже тогда, когда кольцо bent. As в результате смещение, соответствующее изгибающему моменту на фиг. 2 320, 6, равно нулю、 Где находится потенциальная энергия рассматриваемого квадранта?

Для поперечного сечения tpx9, наклоненного под углом < p относительно горизонтального диаметра, изгибающий момент равен 1） , = = И00-ээф) (b） Это подставляется в уравнение для потенциальной энергии (223)、 * ) Моменты, пытающиеся уменьшить начальную кривизну балки, считаются положительными.

Используя формулу (a)、 / [МО» тг(1-so5p)] г * 4 ′ Ко мне. 2 2 л. Два Ля.«- Тангенс. Откуда? МВ-£(*-4′) — ° ’ 182Рг- (224） Подставляя в Формулу (b), получаем: ^ = М(да (с） И. В. По этой формуле можно определить изгибающий момент любого поперечного сечения кольца. Максимальным изгибающим моментом будет точка действия силы P. если подставить

Толстое кольцо. Если размеры поперечного сечения изогнутой балки не малы по сравнению с радиусом кривизны ее axis. It необходимо учитывать не только энергию деформации от изгибающего момента, но и энергию деформации от продольной и поперечной сил. Изменение угла между 2 смежными участками за счет действия пары M основано на Формуле (213) (рис. 321)、 т-она-она» С другой стороны, работа по изгибу пары элементов M, окруженных 2 смежными участками.

Продольная сила N позволяет элементу растягиваться между 2 соседними секциями. Людмила Фирмаль

Равный, увеличьте угол 4 =-1-± J. 0. Если поперечное сечение балки представляет собой прямоугольник шириной b и высотой h, используйте приблизительное значение A * / 12r (см. 311 страниц) для e и используйте a = * 1.2 и£/ C = 2.6.

Находить* 。 \ нпрф 2р .\ (если * 2.12] ’ если h меньше g, то 2-й член в скобках, представляющий влияние на перемещение сил N и Q, пренебрежимо мал и становится ранее полученной формулой(см. стр. 318). Расчет толстых криволинейных стержней приведенная выше теория часто используется для расчета напряжений элементов машин, таких как звенья цепи и проушины(рис.322).

В этих случаях возникают трудности при нахождении закона распределения давления на поверхности балки. Это распределение давления зависит от зазора между мной. Нас ждут болты и изогнутые балки. Удовлетворительное решение задачи может быть получено только при использовании как аналитических, так и экспериментальных методов исследования!). Рисунок 322.

Частный случай люверсов с прямоугольным поперечным сечением (рис. 322) был исследован очень тщательно d). в этом исследовании предполагалось, что зазора не существует, а Болт является абсолютным. Крепко-крепко. Максимальное растягивающее напряжение возникает на внутренней поверхности с поперечным сечением, перпендикулярным оси балки, величина которого выражается формулой: Assah 0 н * РЖ * 8р. Но… (г）

Где Р-суммарная растягивающая сила, передаваемая балкой, а а-численный коэффициент, зависящий от отношения радиуса к радиусу проушины (толщина проушины перпендикулярна плоскости рисунка).Для r  / g, который равен 2 и 4, значение a равно 4,30 и 4,39.Значения напряжений, полученные по Формуле(Е)хорошо согласуются с экспериментом). Теория изгиба тонких колец была применена для расчета фюзеляжных колец конструкции самолетаи жестких колец подводных лодок).

• При расчете деформации криволинейного стержня ранее использовалась теорема Кастшаноано, но эта задача может быть решена введением фиктивных сил, как и в случае прямых стержней. Расчеты особенно упрощаются для тонких стержней, которые могут игнорировать силовое воздействие колонн и стержней. Рассмотрим стержень АВ (рис. 323), который герметично закреплен на конце А и нагружен на его плоскости симметрии xy.

To определите смещение конца B, рассмотрим минутное смещение самолета на этом конце за счет изгиба элементов mn стержня. — Используйте SP ’ Уравнение (214) для определения изменения） — си. Рисунок 323. 2 угла между смежными поперечными направлениями Вид в разрезе, мы найдем Заметив, что бесконечно малый треугольник BCD подобен треугольнику nBnt, находим 2 составляющие этого смещения.

Чтобы получить 2 составляющие полного движения конца Б, нужно выполнить основные движения (!) для всех элементов бара. Вам просто нужно сложить).Обозначим эти компоненты через И и V, и если они положительны, См ’Кг’ (*). Б е г е 11, Митт. Materialprüfungsanstalt, Spec. No. 15. 1931. исследование глаз с использованием фотоупругого метода было проведено с помощью K-Takeshiga и Y. Hosokawa, Rept.

Летчики. Лаборатория (Токио), T. 18, p. a. 128, 1926, M. M. F g os h t and H. No. Ч я 1 ^ Докл. Механик., Т. 7, стр. 5, 1940.In в последней статье мы рассмотрели влияние зазора между болтом и отверстием. * ) У. С Т и я с Д А авиации — Форш, вып.18, p. a. см. 214, 1941.Натуральный. Членом консультативного совета является Авиатор. Технология Мэм. Нет.1004, 1942, Д. А. Дю-Р 1 Н Т 1 е р, Я. см. также аэронавта. СИЭ. том. And, p. 136, 1944; R. B e n j A m i p, Ditto, D. 19, p. 585, 1952 * )

Очень полное исследование таких колец П. Ф. П а-книга О П в, ч, Строительная механика Москвы, т.2, pp. It находится по адресу 1-816, 1947.CMdsCMds м 〜Я гы-(УФ-г),> » = Дж к -). (Я） Оу, оу, оу. Например, на Рис. 1 319 стержень, M-Pr cos .Таким образом, оба конца открытого кольца В этом состоянии внутренний радиус цилиндра затягивается до r, и такое кольцо, вставленное в цилиндр, будет оказывать равномерно распределенное давление на стенку цилиндра). Рисунок 330.

Например, r = 25 см, [aj = 300 кг / см, p = 0,1 кг / см2 No.£= 8-105.кг / см2, определяют 8 и фу для чугунных поршневых колец. Подставляя эти значения в Формулу (ы), получаем ho — 1,6 см, а из Формулы (ов) получаем 6 = 0,29 см. 11. Выведем формулу (321 страница) (227). 12. Рама, состоящая из 2 вертикальных стержней и полукруглого стержня (рисунок ЗЗО), приводится в движение силой P вдоль оси симметрии рамы.

Найти горизонтальную реактивную силу H и изгибающий момент M. точка действия силы P, когда рама имеет определенное поперечное сечение и предполагается h B в опоре Влияние продольной и поперечной деформации> Петли игнорируются. Будь то Решение. Людмила Фирмаль

Величина силы и выводится из уравнения^ = 0.Вы можете просмотреть результаты следующим образом •Ч = хр. M = кгрг、 (в> Где^ — числовой коэффициент, зависящий от соотношения/ / g. некоторые значения этих коэффициентов приведены в таблице 11 ниже. Таблица 11 Значение коэффициента уравнения (v) Я… г. к», к = 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 0.0984 0, С$ 4 0.0857 0.294 0.0754 0.304 0.0669 0.313 0.0598 0.321 0.0537 0.328 0.0486 0.335 0.0442 0.341 0.0403 0.347 зо. 0,0370 0.352. 13.

Решите предыдущую задачу, предположив, что A и B опоры закрыты на краю рамы. Ответ. Значения h и M определяются по формуле (г).Номера коэффициентов приведены в таблице 12. ^Эта теория основана на концепции Н. Р ЕКА 1 * ЭМ, Энн. Мой, 5, 38 страниц, 1874; Компт. раздирать. том.73, стр. а.542, 1871; Е. Р Е я и Н Н А Д Д т, З. Вер. См. также втор. Инг.. т. к.45, p. 232, 1901; H. F g i e d m A n n, Z. osterr. Инг. Архитектор. Версия. том.60, p. a. 632, 1908; Z. Ver. Эй, Инг. том.68, p. a. N для 254, 1924.0, распорные кольца.

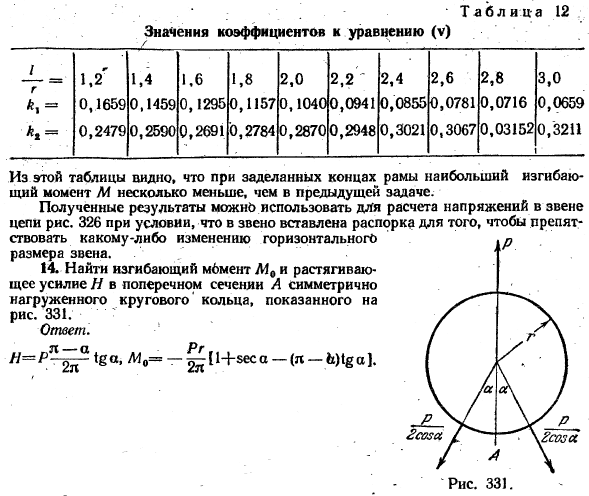
Таблица 12 Значение коэффициента уравнения (V) / * *• Из этой таблицы видно, что максимальный изгибающий момент M несколько меньше, чем при выполнении предыдущей задачи, так как торцы рамы герметизированы. Результаты можно использовать для расчета напряжения звена цепи. 326 предусмотрено, что в звено вставляется распорка для предотвращения изменения горизонтальных размеров звена. РНС. 331. 14.Найти изгиб mbM0 и растягивающее усилие H в поперечном сечении a кругового кольца с симметричной нагрузкой, показанной на рис. 14. 331. Ответ. Н = Р * ’〜ТГА, А10 = — >П+вес — (л-б) 1ба].

Смотрите также:

Предмет сопротивление материалов: сопромат 

Двухшарнирная арка	Изгиб кривых брусьев силами, действующими в плоскости симметрии
Напряжения в ободе махового колеса	Частные случаи изгиба кривых брусьев