Частные случаи изгиба кривых брусьев

Частные случаи изгиба кривых брусьев

В следующем примере показан расчет величины n, которая определяется из уравнения (О§ 77 и расстояния e нейтральной оси от центроида поперечного сечения) для некоторых частных случаев. Зная эти значения, уравнение из предыдущих 2 абзацев••* когда На рис. 3.10

• Прямоугольное поперечное сечение в этом случае ширина поперечного сечения b (рис. 310) постоянна、 — CHY〜* 1 ЧД = СП Ини-ВНТ + — ’T 2 +4 С(г-т ^ р)ды = БР Ф Дж-г — ’У ч 2, 2. Ди. *) Это предположение достаточно согласуется с точным решением узкого прямоугольного сечения. Книга автора теория упругости, стр. 75, 1951.、

Если величина L / r невелика, то расстояние e невелико по сравнению с A, и для вычисления с достаточной точностью по формуле (b) необходимо: Таким образом, вы получаете быстро сходящийся ряд, в котором величины m и e могут быть легко вычислены с произвольной точностью.

Если вы получаете только первый член серии、 Он принимает 1n ^с максимумом accuracy. To устранить это неудобство можно с помощью известных номеров Тогда из Формулы (a) Л * л * Т * * 12г *и * ^ 12г в Если вы получаете 2 членов подряд, вы найдете 4 Л/, 3 ЛМ. 4 люмен mrrr [[1+T^) и e = = T2R (1+T51^)*’ *> Если значение мало, вы можете видеть, что расстояние e очень мало.

Из этой таблицы видно, что при rH2> 10 получаем линейный закон распределения напряжений, а для максимального напряжения можно с достаточной точностью использовать формулу, выведенную для балки прямой оси. Людмила Фирмаль

Тогда вместо гиперболы можно наблюдать линейный закон распределения напряжений с достаточной точностью accuracy. To сравните полученные результаты с этими 2 видами распределений напряжений при прямоугольном сечении, как показано в таблице 8.

Таблица 8 Сравнение гиперболического метода и линейного закона распределения напряжений Г ПГ гиперболический закон распределения напряжений погрешность линейного закона распределения напряжений°Шах*% а п а п \ 9.2 −4.4 6 −6 35.0 2 14.4-10.3 12 −12 \ T; 0 3 20.2-16.1 18-18 10.9 4 26.2 −22.2 24■-24 9.2 10 62.0 −53.0 60 −60 3.2 Трапециевидное сечение.

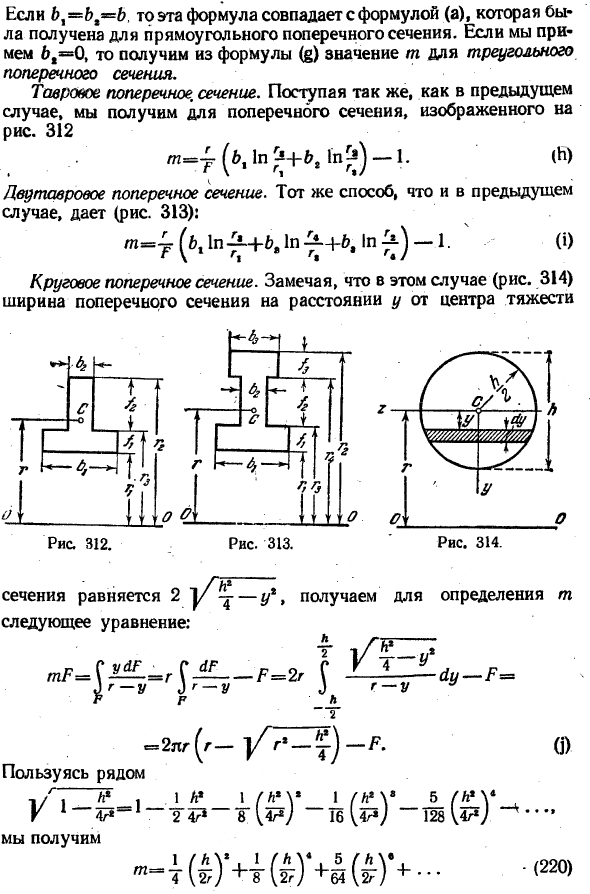
Снова используя уравнение — М-р?, <«> Введение обозначений — Г,(е） Где V-расстояние от вылупления элемента от оси(рис. 311). 00 проходит через центр кривизны оси балки、 Рисунок і i1. (Да Раздел / л / 7 » GG I V G / G ’ При I переменной ширине по горизонтали * 11 9 (рисунок 311) равно И U,(6> — б%) (ч-г） И затем №.[Б, 1-Д]. Возьмите это в уравнение(0、 −7 {[.+ < — .■Цг>] -«•}-Я- (си） Для 6,=&,=&.

Эта формула совпадает с формулой (а), полученной в прямоугольном сечении. Если мы возьмем 61 = 0, то получим из уравнения значение m треугольного сечения. Т-образное поперечное сечение. Действуйте, как и в предыдущем случае, и получите раздел, показанный на картинке. 312. ТТ? ( & > £ * +&, 1П^) −1.(си）

Поперечное сечение двутавровой балки. Получается так же, как и в предыдущем случае(рис. 313）： Я… — ^(d11p + b, 1pD + 6, ip) -.1. (я） Круговой крест section. In в этом случае (рис. 314) обратите внимание на ширину поперечного сечения на расстоянии y от центра тяжести О Рисунок 313. 4. В. — −4. 11. О Рисунок 312. 4! гг. Гї-4-1 1■■* .Г-О » ^ я-4—

Поперечное сечение равно 2 V — — — y1, и мы получаем следующую формулу для определения m: Т / 7： Р Р Л — 2ππ (- УгУг> -))- П.） Польза в конце 1. 1. 1 л * , я(в г _ 1 л#5_ г / л * г V 4l * 247i8 \ 4g) 16 [&) 128 Возьми — II) ’ + 4 (I)’+ -, 2a>) значение mF получается как разность 2 областей, поэтому результат менее точен, и этот метод дает только грубое приближение.

• Гораздо большей точности можно добиться, разделив поперечное сечение на полосы одинаковой ширины и применив правило Симпсона вместо вычисления интеграла по формуле (d) 3). Вышеуказанная теория адвокатского сословия Кривого использована для конструкции поднимаясь крюка).На рисунке 316 показана рабочая часть крюка с постоянным круговым сечением. Перпендикулярная сила P предполагается проходящей через центр кривизны оси крюка.

Максимальное нормальное напряжение изгиба возникает в поперечном сечении, перпендикулярном нагрузке P. затем, как описано в§ 78, можно видеть, что напряжение P добавляется к горизонтальному сечению крюка.* Используя формулу (218), сложив напряжение от центра тяжести поперечного сечения C изгибающим моментом M = Pr силой P и изгибающим моментом M、 ЛЦу-е—, р. Ру Фе(гр)т г ФМ(г-г) ’ Если мы применим эту формулу к самой дальней точке г〜^ rhI2t、 П н _ _ п ч / УП Проверить 2mrt 9 mln_» Ф 2mrt * ’

Вы можете видеть численно, что максимальное напряжение-это растягивающее напряжение на внутренней поверхности, которое получается путем умножения напряжения P / F на коэффициент напряжения. (222) Его значение зависит от соотношения h / 2r. используя выражения Для (220)м вы можете видеть, что k изменяется от 13,5 до 15,4, а h / 2r изменяется от 0,6 до 0,48.Если m определяется с помощью правила Симпсона (4), можно выполнить расчет напряжения для крюка для неправильного участка.

Примеры таких расчетов приведены в статье: A. M. Wahl, J. Appl. Механик., Том 13, стр. 2o9, 1946. ’ * ) Теоретическое и экспериментальное исследование подъемных Крюков проводилось британской Национальной физической лабораторией. H. J. см. о O и G h. Л. Х. Кокс и Д. Г. мыла в З я т, ч, Тез. Докл.-Инст. Мека Engrs. (Лондон), 1934, 12 месяцев.

Для сравнения экспериментальных результатов с теоретическим напряжением крюка прямоугольного сечения, K. Böttcher, Forschungsarb, No. См. 337, 1931. * ) Если L / 2r = 0,6, то значение коэффициента k является минимальным. 4) Этот метод был процитирован А. М. Людмила Фирмаль

Это объясняется Шалом. 315 страниц Задачи Я… для r = 12 см и L = 10 см определите числовое отношение sgmt n в| P. ’I «1.81. ^Тип Ответ. 2.Решает предыдущую задачу круглого сечения. 4> 46 «1.96. — Проверить 0t1p1 5.54 7 Ответ. е = 0.54 см. / •3.Определите размер 6 и b. поперечное сечение двутавровой балки(рис. 313).ATAX и crt1n чистого изгиба численно равны.

Даны следующие размеры: r,= 3 см, 4 см, r4 = b см, r%-1 см, Lr-1 см, Lx 4-L-5 см. Из Формулы(212)、 Г + е. г. г. е. Или / д—Нх — ^е Откуда? г 2г, охранник. = — 7-^ = 4、2 см + 1 г, 4-г、 если мы подставим значение (i)вместо m и заметим, что/ r = 7 / cmg、 7. Откуда? 4.2 =- 611іі-+Мп4 + (5-61) іп-І 4. 7. 6; 1p1-M5-61) 1#1 = q-1./ Золото Или 0.2 Ш,* 0.154 (£- «d-1.677-0.406 = 1.261 см、 ВХ = 3.67 см, т = 5-3. 67 = 1,33 см. 4.Вы можете определить followingBy размер 6, раздел T(рисунок 312), otax и am1n сгибают аккуратно, и числа равны.

Указаны следующие размеры: rx = 3 см, r, −7 см, r9 = 4 см, br = 1 см. Ответ. 5, = 3,09 см. 5.Определите АТАКС и ot_p крючков трапециевидного сечения, показанных на рисунке. 317, если P = 2000 кг, то 5 = 4 см, b: — \ см, gx-3 см、 народный депутат, пред г = 12 см. Решение. Из уравнения _ 22.5 22 секунды, 5 секунд, o ’ = 3,935 см ’ ми= Я + — Е-1°^-(4-1） Радиус оси пучка, следовательно, е = 0.88 см, л—А = Р — Е-Л、= 5.72-3 * −5.72-6.28 см/ ч?= 22.5-0.88 =19, 8 см1, m = изгиб по формуле (2 s 2) равен = 2,72 см, A * 4-g r \ — e-12— См. Рп рп = 13 200 кг. = 604 кг} см1 — Проверить 349 кг} см ’ °t_pg 13200-2.72 19 * 8 * 3 » = 13 200-6. 28 19.8-12

К этим напряжениям, обусловленным изгибом, необходимо добавить равномерно распределенное напряжение от растягивающей силы Р, равное R / g = 2000 / 22,5 = 89 кг / см2. T <полное напряжение В то время °Шер= 604 ^ 89 = 693 кг} см1 «-349 ^ −89 =-260 кг} см*. 6.Найти максимальное натяжение крюка в круговом сечении, если диаметр поперечного сечения равен L = 2,5 см, а радиус оси равен r = 2,5 см, Р = 400 кг. »

Ответ. Атака= 1148 кг! см2. 7. Для A = 10 см, r = 10 см, a = 10 см, P = 2 т найти N и u изогнутой балки с круглым поперечным сечением, с нагрузкой, как показано на рисунке 318. Ответ. атакс = 695 кг! см2 {n =-266 кг! из см2

Решите предыдущую задачу, предположив, что поперечное сечение МП имеет форму, показанную на рисунке 8. 312, следующие размеры: g,= 5 см, g,= 7,5 см, g-22,5 см, 6,= 10 см Lm-2,5 см, a = 10 см, P = 1,6 т Ответ. атакс = 221 кг! см2,^ » ==-114 кг] см2. 9.As как показано на рисунке 7, предположим, что сечение mn представляет собой трапецию и решаем задачу 7. 311, размер Р,= 5 см, F = 10,6 см, 6 = = 5 см, l = 2, б см, О = 0, П = 1,25 т Ответ. Максимум= 646 кг! см2, Макс= −380 кг! см2.

Смотрите также:

Предмет сопротивление материалов: сопромат 

Деформация кривых брусьев	Чистый изгиб кривых брусьев
Двухшарнирная арка	Изгиб кривых брусьев силами, действующими в плоскости симметрии