Чистый изгиб кривых брусьев

Чистый изгиб кривых брусьев

Чистый изгиб изогнутые бар В следующем представлении мы предполагаем, что линия, называемая осью балки, которая соединяет центр тяжести поперечного сечения балки, представляет собой плоскую кривую, и каждое сечение имеет ось симметрии в плоскости этой кривой. 1) поскольку балка подвергается воздействию сил, расположенных на указанной плоскости симметрии, изгиб происходит на той же плоскости.

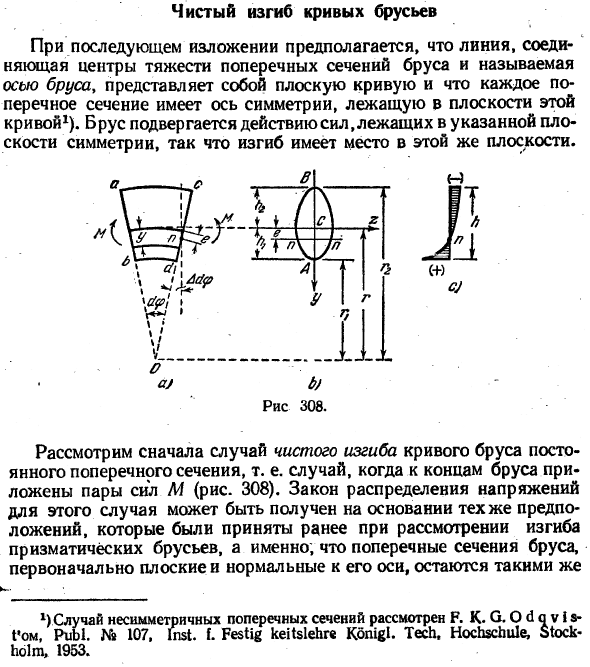
• Да. ЭйДжей. bj. Рисунок 308. Сначала рассмотрим случай чистого изгиба криволинейных балок определенного поперечного сечения, то есть когда к кромке балки приложена пара сил м(рис.308).Закон распределения напряжений в этом случае может быть получен на основе тех же допущений, которые ранее принимались при рассмотрении изгиба призматической балки. Ф. Ладно. Г.

В случае асимметричного сечения был рассмотрен. для D и Q V является т ом, опубл. НСТ 107, Инст. а. Festig keitslehreKönigl. Техник, Высшей Школе, Стокгольм, 1953.Гнуть материал 1). пусть ab и cci — 2 бесконечно близких участка пучка(рис. 308, а), а затем уменьшите угол между ними до bending. By изгибаясь, поперечное сечение L поворачивается на небольшой угол Δі против a b вокруг нейтральной оси nn.

Если начальная кривизна уменьшается при изгибе, то этот угол и соответствующий момент M будут положительными. Людмила Фирмаль

Это вращение сжимает продольные волокна на выпуклой стороне балки и растягивает волокна на вогнутой стороне. Проходя через центр тяжести поперечного сечения, расстояние волокна от оси, перпендикулярной плоскости изгиба, обозначается y, направление к центру кривизны оси пучка показано положительным, расстояние от центра тяжести c до нейтральной оси показано np. l_ (г-е) д * р•(а） (Д-Г).

В этой формуле r обозначает радиус кривизны оси пучка (рис. 308.6), а знаменатель формулы (а) представляет начальную длину волокна между рассматриваемым поперечным сечением ab и she. Предполагая, что между продольными волокнами 2) нет бокового давления, на расстоянии y от центральной оси получают напряжение, перпендикулярное поперечному сечению. £ < Г-Е)Д < * < П-） (р-г) йй>.

Теперь мы можем видеть, что распределение напряжений следует гиперболическому закону, как показано на рисунке 2, а не линейному закону, как в случае изгиба призмы. 308, p. In в случае аккуратного изгиба, из условия, что сумма вертикальных сил, распределенных в сечении, равна нулю, можно сделать вывод, что здесь нейтральная ось перемещается от центра тяжести поперечного сечения к центру кривизны оси балки.

• Если поперечное сечение балки прямоугольное, то площадь штриховки, соответствующая натяжению (рис.308, в), должна быть равна площади штриховки, соответствующей сжатию. 1) это теория приближения Э. Винкля, г-на Цивилингени- евро, объем.4, p. s. 232, 1858; см. Также его книгу » Die Lehre von derElastizitätund Festigkeit«, Прага, 1867 15 дней. Аналогичная теория используется H. R e.- Ром, Энн. Моя, стр. 617, 1862.

Дальнейшее развитие теории связано с тем, что Ф. книга Festigkeit Elastizitätund, Р Грасхоф ом. Сделано в 251, 1878.Увидеть^ д Хантер и Пирсон, история теории упругости, вып. 2, стр. 422, 1893. Для опубликованных работ, связанных с правильным решением проблемы кривых брусьев, автор и Дж.- «Теория упругости» Гуайера, П. см. 63, 1951.

Но она не оказывает существенного влияния на нормальное напряжение из-за bending. It сразу видно, что максимальное напряжение генерируется на вогнутом side. To убедитесь, что напряжения чрезвычайно растянутых и уплотненных волокон равны друг другу, следует использовать форму поперечного сечения с центром тяжести, близким к вогнутой стороне балки.

Точная теория показывает, что существует определенная степень радиального давления. Людмила Фирмаль

Уравнение (b) содержит 2 неизвестные величины. Расстояние e нейтральной оси nn от центра тяжести C (рис. 308, Б) и угол поворота D d м м <1 <rt (r-e) e подруга Подставляя это значение в уравнение (b), получим следующее уравнение для нормального напряжения: _ М {Г-Е)М(Г-Е)φ1 ^ р(р-е)е(р-г)ее(р-г）* Для определения напряжений самых дальних волокон вместо точек A и B (рис.308.6) получаем значения (/=6, и y= -). Mph^,^ е) (212） 。 ЭЭГ *в G Eg 9, ’ 7 Здесь hl и r%означают радиус внутренней и внешней поверхностей криволинейных балок.

После того, как вы определили величины m и e из уравнений (0 и (209)) для заданной формы сечения, вы можете легко вычислить нормальное напряжение, используя уравнение(211). Изменение угла между 2 последовательными поперечными сечениями< / < p D k получается из уравнения (210).

Соответствующее изменение кривизны оси балки Д <1ph м _A4(Т + 1） (213)） — <15 исполняемый■»тг * ээ * Если радиальный размер изогнутой балки H мал по сравнению с радиусом кривизны r оси балки, то можно сделать вывод, что если величиной y пренебречь по сравнению с r в формуле (0 и t), а радиус кривизны становится все больше, то число m приближается к нулю. Тогда выражение (213), представляющее изменение кривизны оси балки, приближается к значению (214)） Ее g * k ’ Это соответствует ранее полученному значению кривизны стержней первой прямой (см. стр. 123).

Смотрите также:

Предмет сопротивление материалов: сопромат 

Изгиб кривых брусьев силами, действующими в плоскости симметрии	Теорема о взаимности работ и перемещений
Частные случаи изгиба кривых брусьев	Исключительные случаи