Оглавление:
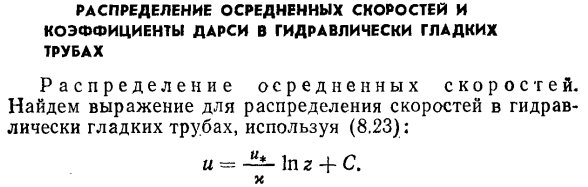



Распределение осредненных скоростей и коэффициенты Дарси в гидравлически гладких трубах
Распределение осредненных скоростей и коэффициенты Дарси в гидравлически гладких трубах. Распределение средней скорости. Используя (8.23), найти уравнение распределения скоростей для гидравлически гладкой трубы. И-1П г + с Икс 166. Для определения константы с примените (8.23) к точке на внешней границе вязкого подслоя. Где r = bv; bv =Λ^***.И затем… «Вход= 1Н 6В ч-с(8.34) Икс БВ = ЛФ? Учитывая /и*, можно записать C = Li * 1n = u * (’m-1n N)-1n -. Я »* V К / Я.
Для гидравлически гладких труб коэффициент Дарси не зависит от шероховатости стенок. Людмила Фирмаль
- Подставляя эту формулу в (8.34), получаем относительную локальную скорость гидравлически гладкой трубы(при x = 0.4 и N = 11.6) -= 5.75]§^-+5.5。 (8.35) * В С гидравлически гладкими трубами, по мере увеличения числа Кэ, участок скорости становится все более «полным» (рис.8.4,таблица 8.2). Таблица 8. 2 Коэффициент Дарси я нахожусь в гидравлически гладкой pipe.
To определим коэффициент H, формулу логарифмического распределения скорости трубы гидравлически гладкой (8.23) применяем к точке на оси трубы (u = itach, r = r0), или формулу локального дефицита скорости от максимума(8.24) до границы вязкого подслоя(r = bv-ЛЛ / / n *; u = VV〜).Результат (Itach / и * формулы) будет таким же. Используйте формулы (8.25) и (8.35) для определения коэффициента Дарси первым способом. О r = r0 из (8.35) −5,751§ ^ -+ 5Д В. 167.
- Замена дефицита выражением, принимая во внимание, что B> = 3,75. О И* ^ = 5,751§+ 1,75 в. + 1.75. (8.36) (7.24) напомним, что y /and= = U8D заменяют»* » под логарифмом на y ^ K / 8 и r0 на^ / 2. После подсчета ^ =2.03 1§ключ −0.91. Для гидравлической гладкой трубы, она должна быть изменена согласно экспериментальным данным и использовать Jagle согласно (8.36). −21§нет-0.8(8.37) Г ^ гл Или = 21П ^%Д-. ’(8.37 а) К * * Л 2 ′ 51.
Выражение (8.37) подразумевает связь между жонглированием и нет. Более удобным является выражение, в котором представлены явные зависимости a, ch от He. Т. 0.3164 Ke0 ′ 25 ′ (8.38)) Официальное жонглирование, предложенное в 1913 году Блазиусом, имеет следующую форму: Где Кэ = ПФО.
Как видно из последней формулы, потери напора прямо пропорциональны скорости во второй степени, поэтому эта область и носит название квадратичной области сопротивления. Людмила Фирмаль
- Эта формула для 4000 дает результат, который хорошо согласуется с экспериментальными данными. При замене (8.38) на (7.19) потеря давления по длине составит 1,75 градуса пропорционально средней скорости, если труба гидравлически гладкая. 168. Форма формулы колбурга является
Смотрите также:
Возможно эти страницы вам будут полезны:
- Гидравлически гладкие и шероховатые трубы (русла). Толщина вязкого подслоя.
- Экспериментальное изучение коэффициента Дарси.
- Распределение осредненных скоростей и коэффициент Дарси в гидравлически шероховатых трубах. Переходная область.
- Коэффициенты Дарси для труб с естественной технической шероховатостью

