Оглавление:








Приложение теоремы Кастилиано к решению статически неопределимых задач
Применение теоремы Кастильского нано к решению статически неопределимых задач Теорема Кастильяно также очень полезна для решения статически неопределенных задач.Запускает задачу, в которой отклик поддержки считается статически неопределенной величиной. Х> Г.
- Если вы указываете силу реакции, которая не может быть определена статически, вы можете представить энергию деформации системы в виде функции от них forces.In в случае неподвижных опор и опор, движение которых перпендикулярно направлению реакции, частичная производная энергии деформации для неизвестной силы реакции должна быть равна нулю по карти-theorem.So … Ди / • * * ‘ л дц л-Ди — / л / пр’zi •я /-* * Таким образом, вы получите такое же количество уравнений со статически неопределенной реакцией.
Показано, что уравнение (203) представляет собой условие функции и, следовательно, реактивное значение, которое является статически неопределенным.Власть подобна осколкам потенциальной энергии системы.Это принцип так называемой минимальной работы, который применяется для определения ненужных реакций 1).
В качестве примера применения вышеуказанного принципа рассмотрим равномерно нагруженную балку, которая герметизирована на одном конце и свободно поддерживается на другом конце (рис. 287).Есть 1 причины для этого. ■ Реакции, которые нельзя определить мягко.Найти эту неизвестную силу из уравнения с соответствующей опорной реакцией X как статически неопределенную величину.
Рисунок 287. (ля) j} согласно jurmule(190), потенциальная энергия пучка равна / м = Х Х-Х〜. Куда? (Си) когда (A) заменяется、 Мне. Я (ХХ〜Ç) xdx = Вт (х Т-СН4) Откуда? КЛ. Вместо силы реакции X можно рассматривать реакционную пару Ma на левом краю пучка как статически неопределенную amount.In в этом случае энергия деформации становится функцией Ма.Формула (b) сохраняется, но изгибающий момент любого сечения равен Производная энергии деформации по Ма, основанная на условии, что левый край балки не вращается при ее изгибе, равна.
Минимальный принцип работы-статья Ф. Мепеж «Nouveau principe sur la distribution desensitions dans lessystèmesélastiques», Компт. раздирать., т. к. 46, p. 1056, 1858; там же.том.98, С.Увидеть 714.1884..
Полное доказательство принципа было дано кастильским, который сделал этот принцип основным методом решения статически неопределенных систем Людмила Фирмаль
Применение метода потенциальной энергии в технологии выглядит следующим образом: Mög (цитируется Abhandlungen), H. Muller-Die neuren Methoden der Festigkeitslehre по Breslau и F. Engcsser’omüberdie был разработан Berechnung statistich unbestimmter. Система», Центр. Баувервальт.А п. а.606, 1907.Очень полную справку по этому вопросу можно найти в INM.Gruning статья Encyklopädieder Mathematischen Wissenschaft, Том 4, p.It можно найти в 419.
Равны нулю, т. е. литий {МШ gtsmsch、 дуплексный. немецкая марка. Л н EJ \ 24 3) u * Где я могу получить абсолютное значение момента М » = 4 Используя теорему Ка-стилиано, можно также решить задачу о принятии в качестве статической неопределенной величины силы, действующей на дополнительный стержень системы.Например, рассмотрим систему, показанную на схеме. 18, Это было объяснено ранее (см. стр. 26).
Если принять силу X вертикального стержня, величину которой нельзя определить статически, то можно увидеть, что сила наклонена У/У/ШУ//,С Да. Б.) С. х. Бары ОВ и ОО равны a• Энергия деформации наклонного стержня (рис. 288, а) и (рис. 288, 6) вертикального стержня дают полную энергию деформации системы 1) и-И ‘+ и’-(£БЖ)(=> Если узел O действительно движется вниз на рисунке 18, производная энергии C / \системы, показанной на рисунке 18, к X должна быть равна-b при 288.
Это связано с тем, что сила X системы находится в противоположном направлении от направления движения B. увидимся. ди9 л. * Потому что производная равна b、 ^ = Т + С = — Е + 6 = °- (д) Видно, что истинная величина избыточной стержневой силы X такова, что она производит полную энергию деформации системы минимунтом. Если вы замените выражение (c) на выражение (d) вместо U, вы получите: _ П-Х I ХІ Q 2cosx a f’e cosaEE* 1) предполагается, что все стержни имеют одинаковую площадь поперечного сечения ГУ E X тот же модуль, что и сечение = Откуда?
Аналогичное рассуждение может быть применено к статически неопределенной системе с 1 дополнительным стержнем, и можно утверждать, что мощность этого стержня такова, что он изменяет энергию деформации системы на a minimum.In чтобы объяснить, как рассчитать силу в такой системе, рассмотрим рамку, показанную на рисунке. 289 a.реакция здесь может быть определена статически, но если вы попытаетесь определить силу стержня, вы увидите, что есть 1 дополнительный стержень.
- Мы берем ядро компакт-диска дополнительно. Рисунок 289. О, X D. Я… 1 а 7 3 I V X 1 * в Стержень в любой точке и применить к каждому концу?И \ \ сила X, равная силе стержня. Таким образом, мы достигаем статически определенной системы, которая получает действие неизвестной силы X в дополнение к известной силе P. мощность стержней этой системы определяется в 2 этапа. 289, 6), и обозначается 5° -, где/обозначает номер стержня. 2) внешняя сила P отбрасывается, сила, равная 1, возникает при замене ее силой X (рис. 289, в).
Конечное усилие обозначается цифрой 5′.Тогда суммарная сила любого стержня при одновременном действии силы Р и Силы Х、 (ми)) Суммарная потенциальная энергия системы по формуле (199) 、 , 1Yφ/’ ^”(£?±£М т И — £ * 2 2 T:E 9 Я»1 /Я」
Здесь сумма распространяется на все стержни системы, включая отрезанный стержень x).Здесь мы применяем теорему Кастильяно.В соответствии с этим производная U относительно X смещает концы F и F \из одного направления в другое. other.In дело в том, что стержень не режется, и это движение равно нулю.Отсюда Джей-0′ ® То есть мощность избыточного стержня х такова, что он изменяет потенциальную энергию системы до минимума.
Из уравнения(0 и (g)、 1 = т Далли. = 0、 дх Д- » 2Ф£ Г.-Е. 1 = 1 * я Откуда? Все сходится. (204) я = МС ‘ 4: 2°или 1 = 1 rlc Этот метод может быть распространен на систему, в которой имеется несколько дополнительных стержней. Принцип минимальной работы также может быть применен, если количество статических неизвестных составляет пару forces.As в качестве примера рассмотрим равномерно нагруженную балку с 3 опорами (рис.290).
Получая изгибающий момент на промежуточной опоре статически в виде неопределенной величины и разрезая балку на B, 2 балки с неизвестной силой пары Mi нагружаются свободно лежа на опоре, за исключением известной равномерной нагрузки q (рис. 290.6).Потому что изогнутая ось балки является непрерывным, Нет вращения»Луч»Б энд Б до конца Б.»луч б» с пмсх К Рисунок 290 дю. = 0. (205)) немецкая марка.
Опять же, статически неопределенное количество значений похоже на изменение энергии положения системы до минимума. Людмила Фирмаль
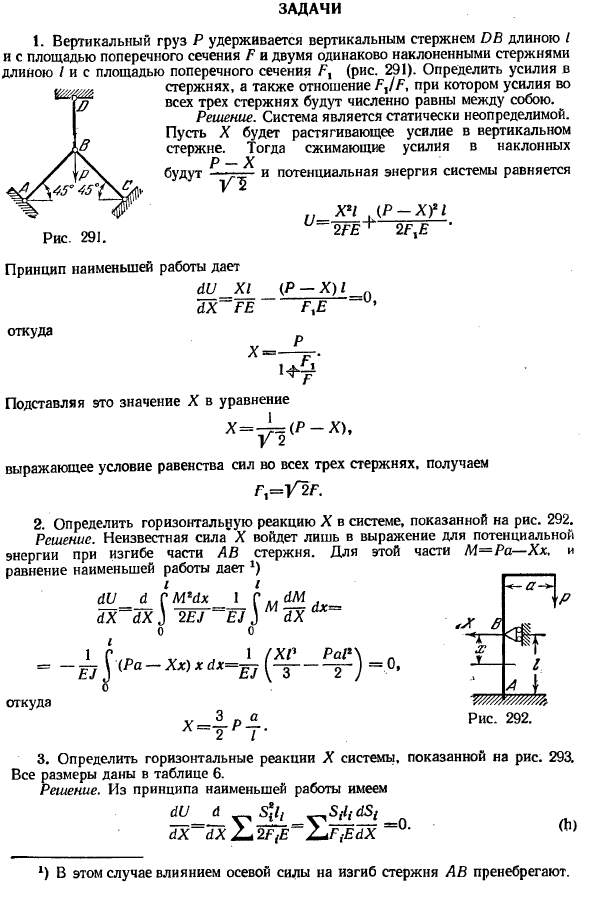
1) для этого стержня 5 * = 0 и S {= 1 Задачи !Вертикальная нагрузка P удерживается перпендикулярным стержнем O B поперечного сечения P длиной I и 2 равно наклонными стержнями поперечного сечения B длиной I(рис.291).Определение инициатив Стержень, а 3 стержня имеют отношение Px /P, при котором все силы численно равны между собой.
Решение.Система не может быть определена статически. Пусть X-растягивающее усилие вертикального стержня.Тогда сила сжатия наклонного p x y, и потенциальная энергия системы Hg1 LR-HG1 И.- 2 PXE загрузки 2 RE Принцип минимальной работы、 W_X1. (PX) 1 РПП. = 0、 А-РЕ Откуда? Икс Присвоить значение Х в уравнение X = Y = A-X) Если выразить условия силы, равные всем 3 стержням, то: GC = U2P. 2.Определите горизонтальную реакцию X системы, показанной на рисунке. 292.
Решение.Неизвестная сила X входит только в выражение потенциальной энергии при изгибе части AV Rod.In эта часть, M = Pa-Xx, и равенство минимальной работы дает). /// <1X (IX J 2£Y ejs когда Да. Л. Икс Один. EJ \ 3 когда Л. Рисунок 292. Откуда? — £ХХ)ХС!Х = Тгн(^ Т AГМЧх [_^m w AH- В А Р Л 2 грамма 3.
Определите горизонтальную реакцию X системы, показанной на рисунке. 293.Все размеры приведены в таблице 6. Решение.Исходя из принципа минимальной работы, мы Любовь. (Си) х ax2 * 2р(е 2 * п еах *) В этом случае, влияние осевой силы на изгиб стержня АВ игнорируется.
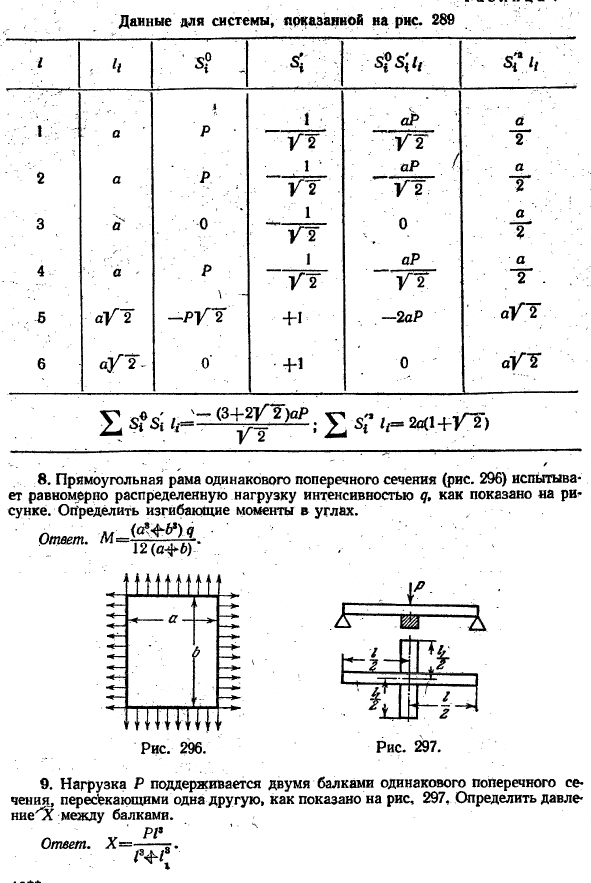
Данные фермы показаны на рисунке. 293. / і » cmP1pcm 2 5 <°. 5і 5 (°в; і, р, » Г и 1 2 3 4 5 6 7 1 360.6 25 -1.803 P + 1.202 -31.24 P 20.82 2 316.2 15,+І.581Р-2.108-70.26 НЬЮ-ЙОРК-93.68 3 100.0 10 + 1.000 с-1.333-13.34; 17.78 4 360.6 25-1. 803 J + 1.202 -31.24 P 20.82. 5 316.2 15 +1.58 І І-2.108-70. 26Х216. 34Р-93.68 2 = 246.78 При X = 0 сила стержня/, вызванная известной нагрузкой P, равна 5^, а сила, порожденная в том же стержне силой, равной 1, заменяющей силу X, равна 5 ^(Рис.293.6).Значения 5 ^и 5 *определяются из статики.Они показаны в колонках 6 и b таблицы 4.
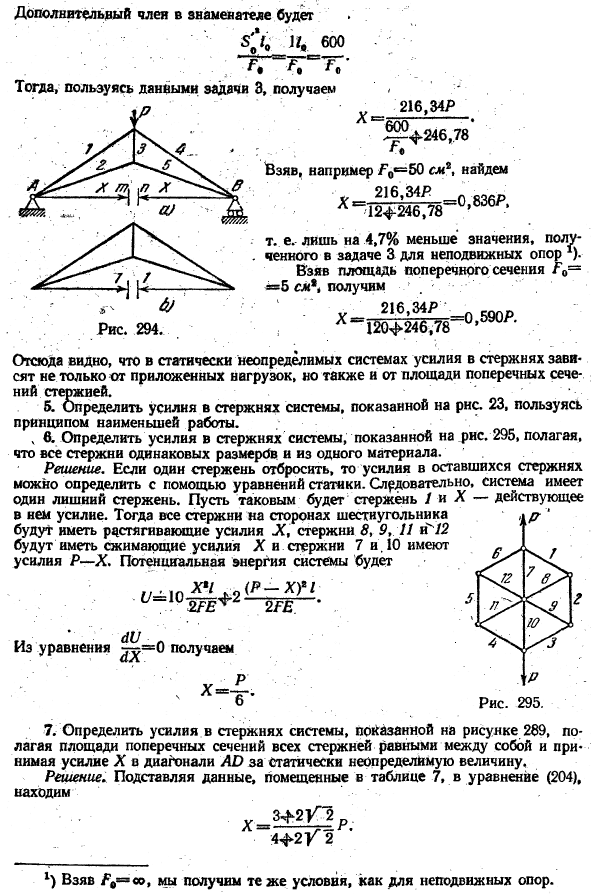
Тогда общая сила стержня равна 5,= ^ + 5’x. При замене в Формуле(б)、 2 ^ ^ II Откуда? «=5 L“ 4 = 5 Фі GI. я-1. Числа, необходимые для вычисления X, приведены в Столбцах 6 и 7 таблицы 6.Если мы подставим эти данные в формулу (i)、 Х = 0,877 П. 4.Определите силу превышения горизонтального стержня системы, которая показана на рисунке. 294, предположим, что длина этого стержня равна 6 м, а площадь поперечного сечения равна P0.
Остальные стержни имеют те же размеры, что и в задаче 3. Решение.Усилие горизонтальной штанги(номер штанги 0) рассчитывается по формуле (204).Эта формула аналогична уравнению 3 С), за исключением системы, показанной на рис. 3. 294, имеется дополнительный горизонтальный стержень 0.Сила, создаваемая в этом стержне только от 1 Силы P (X = 0), равна нулю, t или 5® = 0.Сила, вызванная равными 2 силами Единица измерения (рис. 294.6), равная$ 0 = 1.Сложение числителя в уравнении 0) является сложением знаменателя 1СЧ 600 ; ;
Затем используя данные выпуска 3、 216.34 Дж — 600. Т. ^ -246.78 Например, если вы используете cm2、 ■ 216.34 ч ^ 9LR, п То есть, значение, полученное в фиксированном выпуске поддержки 3, на 4,7% меньше I). Если объявить поперечное сечение f0 = 5 см9, то оно выглядит так: у 216.34 * Соло 1204-246. 78’*.. Это показывает, что в статически неопределенной системе сила стержня зависит не только от приложенной нагрузки, но и от площади поперечного сечения стержня.
Что это? а. определите мощность стержня в системе, которая показана на рисунке. 23, используйте принцип минимальной работы. C. определите мощность стержня в системе, которая показана на рисунке. 295, предположим, что все стержни имеют одинаковый размер и одинаковый материал.
Решение. Если 1 стержень отбрасывается, сила оставшегося стержня может быть определена с помощью статического equation.As в результате система имеет 1 дополнительное ядро.Пусть это будет стержень 1 и сила, действующая на X. Далее, все стержни со стороны шестиугольника имеют натяжение X, а стержни 8, 9, 11, 12 имеют сжатие X, а стержни 7 и 10 человек оказывают I-L. потенциальной энергии системы недостаточно. е / 47.
Извините. С. С. Рисунок 295. Число Yu * u2 UT 2. / 6 Ай-2-Рут +1,. — 2sR aU2 » 6 aU T. 0 ‘ — и 0 aUU С,^ 5 ‘ ИИ = — — — АП + ^ 2); £5,»/,= Ми + ыть」) » > » , * #■/ 8.Прямоугольная рама с таким же поперечным сечением (рис.296) подвергается равномерно распределенной нагрузке прочности<7, как показано на рисунке.Определите изгибающий момент угла. Ответ. 12(А + Б)..- . Тсс. £ в Рисунок 296. Рисунок 297.
Нагрузка Р поддерживается 297 двумя балками одинакового поперечного сечения, которые пересекаются между собой.Определите давление X между балками. P1910.Найдите статически неопределенное значение I в кадре, показанном на рисунке. 170, С. С. 168, используя принцип минимальной работы. Решение.Энергия деформации изгиба рамы 2 EJ. Здесь M0 означает изгибающий момент, который изменяется по длине горизонтального стержня AB и виден в случае балки, свободно лежащей на опоре.
Подставляя в уравнение И затем Я все выясню. когда 2И Л8, ЯЛ2 / л.. 57, Т * ‘ — А〜З] ^•(Т) Интеграл справа представляет собой площадь треугольной диаграммы следующего момента. го р. Балка, на которую была загружена мощность R.Следовательно、 / Два ПК М0(Ф-С). Подставляя в Формулу (w), вы получаете ту же формулу для I, что и для Формулы (114).
Найдите статически неопределенное значение в кадре, показанном на рисунке Боты. На рисунках 169, 172 и 174 используется принцип минимума 12.Найти изгибающий момент Mi балки, показанной на рисунке. 290, установка 2 / .. ‘
Смотрите также:
Предмет сопротивление материалов: сопромат
| Теорема о взаимности работ и перемещений | Теорема Кастилиано |
| Исключительные случаи | Деформация ферм |

