Деформация ферм

Деформация ферм

Варианты фермы Теорема Кастильяно особенно полезна. Определение фермы variants. As в качестве примера рассмотрим случай, показанный на рисунке. 282.Все стержни системы пронумерованы, их длина и площадь поперечного сечения указаны в таблице 5.

• Сила, вызванная силой любого стержня I системы P19 P%RP » можно рассчитать из обычных уравнений статики. Эти усилия показаны в таблице 5 в 4-й колонке. Согласно формуле<171), потенциальная энергия деформации стержня равна 5 ^Г / 2 /г1 -£.Далее, количество позиционной энергии Вся система будет D. • ’. • / = » ^ … 7、 ‘»、•…… .г。. * Т’%. ！ В.

Здесь сумма распространяется на все стержни системы, здесь/ l * = I, а сила является функцией нагрузки P, поэтому, исходя из Формулы (197), прогиб под нагрузкой Pn 6P равен. Штанга / нагрузка равны до 1 и приложены к положению Pn. In будущее, эти производные обозначаются через 5/.Формула для расчета деформации выглядит следующим образом: я = т Распределение нагрузки P / 3 ХV * В 2 в // \ П — з Р2-з Р3 = 4l7 — х-Г, Е•(201）

Используйте этот факт, когда вы найдете указанный деректив. Людмила Фирмаль

Например, рассмотрим деформацию b2, соответствующую силе в точке A на Рис.2. 282a. значения, помещенные в колонку 5 таблицы, были получены с помощью статического анализа в состоянии нагрузки, показанном на Рис. 5. 282.6, будут ли уничтожены и применены все активные силы? Шарнир вертикальное усилие 1 тонна.

Значения, помещенные в столбец 6 таблицы, вычисляются из значений, содержащихся в Столбцах 2-5.Сумма и деление по модулю£=(2/1000) «10W / sr2 Таблица 5 Данные фермы показаны на рисунке. 282. Билайн. s * s; гл. 1 2 3 4 5 6 7 1 500 30-13. 75–0.625 143 0 2 300 15 * + 8.25 4-0.375 62 1 3 400 10. 4-8. 00 0 0 0 4 300 15 + 8.25 4-0.375 62 1 5500 10 4- 3.75 4-0.625 117•0 6500 20-10. 50 −0.750 24 0 7500 10 4-6. 25. 4-0. 625 195-0 8 300 15 4 * 6.75 4-0 примерно.75 51. 9400 10 4- 4.00 0 0•0 10500 30 −11.25•-0.625 117 0 11300 15 4- 6.75 +0.375 51 0 я = ту ^ — A ’»’ = 622 Т / см. = = 1 

Дайте преобразование к (уравнению (201）） х 822-1000 ДГ-2-10с = = ^ » 411 СЛ <. Я… Предыдущие соображения для расчета смещения 61, 6a, соответствующего заданной внешней силе P19 I При исследовании деформации упругой системы необходимо рассчитать смещение точки без нагрузки вообще или смещение точки нагрузки, отличной от направления нагрузки.

• Метод Кастильяно также может быть применен here. At эта точка, дополнительная бесконечная мнимая нагрузка. Получить смещение и вычислить производную^.С этим. Производная требует, чтобы дополнительная нагрузка C была установлена на ноль, а затем определяет желаемое движение.

Например, ферма, показанная на рисунке 1, определяет смещения 282, a и a points. At в этой точке приложите горизонтальную силу f и получите соответствующее горизонтальное смещение << » Здесь сумма распространяется на все стержни системы. Поскольку дополнительная нагрузка<3 равна нулю, то сила I уравнения (а)имеет тот же смысл, что и раньше, а производная равна 282, Р получено как усилие стержня фермы, вызванное нагрузкой, показанной на рисунке.

В 1 / 5а / га/ 4 \-* 000 / 8.25-300、8.25-300 \ л-1as с-Л. 。 b * = £ (^*77Г2Ло * с15 — > −15 -;=°.165. **• ％ При изучении деформации фермы иногда необходимо знать изменение расстояния между двумя точками системы. Эго может быть получено с помощью метода Кастильяно.

Эти значения помещаются в 7-й столбец таблицы. Подставляя эти усилия в формулу (а), видим, что горизонтальное перемещение а равно сумме удлинений 2 и 4 стержней. Людмила Фирмаль

Например, определим, что увеличение расстояния между узлом а и узлом в (рис. 283, а) вызвано силой II, R, Ra. In к этим узлам мы применяем 2 равные и противоположные мнимые силы(?Как показано на рисунке. Из теоремы Кастильяно частные производные являются ( ^ ) d_0 обеспечивает уменьшение расстояния AB, вызванного нагрузкой Яр I» Я,.

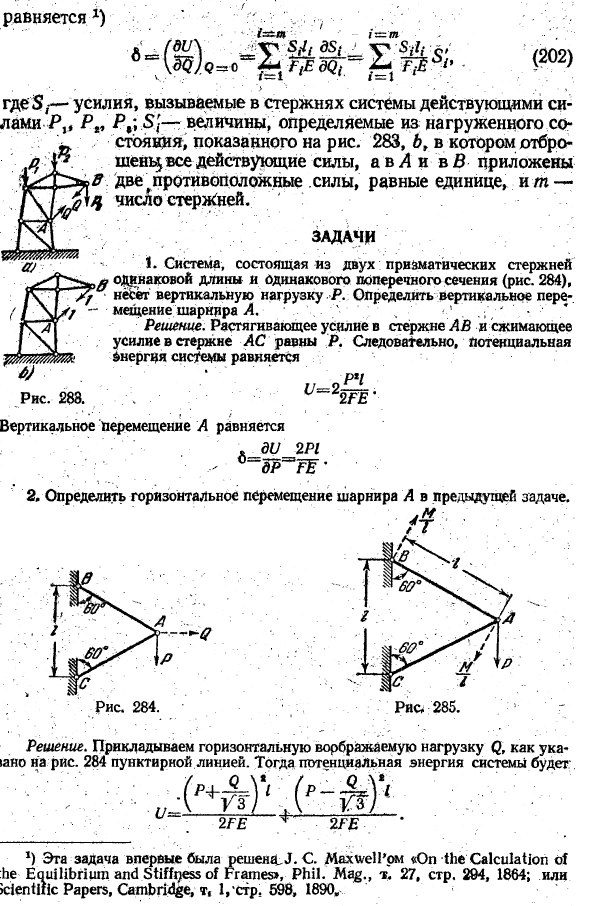
Используя формулу (197), смещение I ^ V M y4 5 ^ * V / г = о б. (202） Где 8-сила, наведенная на стержень системы действующей силой P, # P» I#.5 значения, определяемые из состояния нагрузки, показанного на рисунке 283, б, все активные силы отклоняются, АВ и в прикладываются к силе, равной 2 противодействующим силам, 1, м — число стержней. »

Задачи 1. Система, состоящая из 2 колонн: прямоугольных колонн одинаковой длины и одинакового поперечного сечения 0 (рис. 284）、 * Удерживает вертикальную нагрузку R. * * определяет вертикальное перемещение сустава A…. ’* ;». г’•>’ * ’ Тебе решать. Стержень A B растягивающее усилие и сила сжатия. Мощность стержня переменного тока будет равна R.

Таким образом, потенциальная энергия системы будет выглядеть следующим образом: Рг1. — ■’//-2 ——- 。 ; * °°g2EE ’ Рисунок 288. … • * * » * * ? / Вертикальные смещения равна * дю 2 Р1 2, Определите горизонтальное перемещение шарнира A в предыдущей задаче. ДМ:. • / Т•. The solution. As как показано на Рис. 2, применяется горизонтальная вращательная нагрузка менее 2. 284 пунктирные линии.

И потенциальная энергия системы < üei （ / ч Узу 2FE 2FE *) Эта проблема была решена в первую очередь. J. C. Maxwell ’pM»о расчете равновесия и жесткости рамы», Фил. Журнал. том.27, p. 294, 1864; or krientry Papers, Cambridge, t, 1, ’ Cip. 598, 1890. ой =(Щ)»=•» (.(Щ) » Р=. 3.Определить угловое смещение лекарственного стержня, вызванное нагрузкой Р(рис. 28″.■/,;.： Р п и круг.

Приложите к системе пару воображаемых сил, м, как показано пунктирной линией на рисунке. Иди. Соответствующей этой паре сил, происходит угловое смещение в стержне AE’xn нагрузки A. мощность стержня Выглядит это так:■ стержни AB и Р-у^ \^ ^ Р * * 16 потенциалов ГИА равных — Амги — ’ глгл Откуда? (Определите вертикальное смещение стальной фермы в точке А и горизонтальное смещение точки с, показанное на рисунке. Для 286, P-1000 / sr, площадь поперечного сечения сжатого стержня составляет 30 см, а площадь поперечного сечения растянутого стержня-12 см.

Смотрите также:

Предмет сопротивление материалов: сопромат 

Приложение теоремы Кастилиано к решению статически неопределимых задач	Общее выражение энергии деформации
Теорема о взаимности работ и перемещений	Теорема Кастилиано