Теорема Кастилиано

Теорема Кастилиано

Теорема Кастильяно Используя формулу потенциальной энергии в различных случаях, можно установить очень простой метод расчета смещения точек при деформации упругого тела. Например, для простого натяжения (см. Рис. 1) энергия положения стержня равна * )

• В этом расчете изменение температуры из-за деформации является impractical. To см. далее, t. W e rauch, Theorie elastischerKörper, Leipzig, P. см. 163 и 1884.Смотрите также Architek. Вы Ingenierw,, t, 54, PP. 91 и 277, 1908, ri: p * i Если мы получим производную этого выражения относительно P, то получим: < Р / Р1 ^ * * ■ ДЖЕНЕРАЛ ЭЛЕКТРИК.

Так, производной позиционной энергии относительно силы является смещение, соответствующее силе, то есть смещение приложенной точки меньше 5 или в направлении действия силы. Если консоль загружается последней, то потенциальные энергии будут равны (Формула (ы), p> 268） •* ’. ’•* 4、-％•*。

Производная этой формулы относительно силы P * дает известное отклонение на свободном конце Pl $ ISEJ. 。 * В случае кручения круглого вала, потенциальная энергия равна(формула (185）） И-гги » Производная крутящего момента этого уравнения имеет вид、 Ли мл ГСП. ЩЧ Ф.’ То есть, это угол поворота вала, который представляет собой движение, соответствующее моменту. Если упругое тело подвергается воздействию нескольких сил, то можно рассчитать смещение таким же образом.

Например, выражение © в предыдущем пункте указывает потенциальную энергию луча. Частная производная от этой формулы к силе Р дает прогиб под действием силы.»Частная производная от момента M дает угол поворота опорного участка, на который действует сила M. 。

Теорема Кастильяно является общим представлением этих результатов 1. Людмила Фирмаль

Если материал следует закону крюка и смещение при деформации настолько мало, что им можно пренебречь при рассмотрении действия силы, то потенциальная энергия такой системы может быть выражена функцией 2-го порядка действующей силы (см.§ 71).

В свою очередь, частная производная энергии положения относительно силы дает смещение, соответствующее этой силе Statmo Кастиглиано, Nuovateorîaintorno delJ л’экуилибрио дей сис * Терни упругой! Эйт! «Совет Европы. sci. Торино, 1876.См. также его «téky de pequi bère de símes elasticsé», Torino, 1879. (Для исключительных случаев см.§ 76)»термин» и ^ смещение*могут иметь здесь обобщенное значение.

Это включает в себя тару силы, соответственно,»и» угловое смещение». Рассмотрим общие случаи, которые доказаны на рисунке. 273.Потенциальная энергия-это мощность A, Pa, P,…предполагается, что она выражается в виде функции ：• Р * Р«.). — L (секунды).

Учитывая небольшой приращение 6рп к внешней прочности РП, энергия деформации также увеличивается и ее новое значение 0 +% — <1Рн. (Си） Но количество потенциальной энергии зависит не от порядка, в котором силы приложены к телу, а только от конечного значения. Например, на первой минуте силу yPY9 применяется, то силы р, р *, р *,…Можно предположить, что это было применено.

• Количество конечной потенциальной энергии будет таким же. Сила первого приложенного Рю вызывает лишь незначительное смещение, поэтому соответствующая работа(равная произведению малой силы и соответствующего малого смещения) бесконечно мала 2-й величиной, которой можно пренебречь. Здесь, Сила P, P#, P,…(1Pn 1), и работа, выполняемая этими силами, равна V (формула(a)) тем не менее, если эти силы приложены, Сила (1 и bppn 6 в направлении направления работы, 6 Р генерируется.

Равны друг другу. Поэтому^ ＆ н. В. м * я 。 Для «= 5Р-П» (197） Рисунок 274. И теорема Кастильяно доказана. В качестве приложения теоремы рассмотрим кантилевер, нагруженный силой P, и, наконец, пару сил Ma(рис.274).Изгибающий момент поперечного сечения стремится к M = — Px-My, а потенциальная энергия по формуле (187)выглядит так: О Как получить отклонение b в консоли.

Он основан на условиях, предписанных на стр. 275.Исходя из этого условия, потенциальная энергия была получена как равномерная функция 2-й стенки. Частная производная (1п по г) * LADM a di ’ 1 DR MDR ’ Если вы подставляете выражение в соответствии с I и M вместо M、 * Я… = ^ | (РХ + Ма) xc1x ^ +%. 6. Такое же выражение можно получить, используя один из предыдущих методов, например, метод анализа графа или метод интегрирования дифференциальных уравнений (79) упругих кривых. ■ м： И затем т. т.

Найти частную производную потенциальной энергии относительно силовой пары Ма для получения угла поворота конца. ’- ый-ги МШ; <БН-Х1 $ <Р * + М-> ^ М + 1■¥ О, да. Положительные знаки, полученные для 6 и 0, указывают на то, что отклонение конечного поворота имеет то же направление, что и в паре сила и усилие на Рис.1. 274. НЕМЕЦКАЯ МАРКА.」_ Частичная фракция является.

Скорость нарастания момента M с увеличением силы P показана на Рис. 1 275, а. частные производные Таким образом, он может быть представлен графически на следующем графике: 0 / и» Рисунок изгибающий момент 275, б. использование вывески： немецкая марка. немецкая марка… ЕР = МР. А) легче сначала дифференцировать под знаком интеграла, чем сначала вычислить Интеграл и затем дифференцировать его.

Предыдущие результаты можно просмотреть в следующем формате: Я… 6 = 5? C mm LS 0 =£71 MM ’ ^ x. (198） О. о. Эти уравнения были выведены для частного случая, показанного на рисунке. 274 также полезно для общего случая лучей с любой нагрузкой и любым support. It может также использоваться для распределенных нагрузок.

Однако если нагрузка распределена равномерно, то отсутствует вертикальная сила, действующая в середине балки и соответствующая требуемому отклонению в центре. Людмила Фирмаль

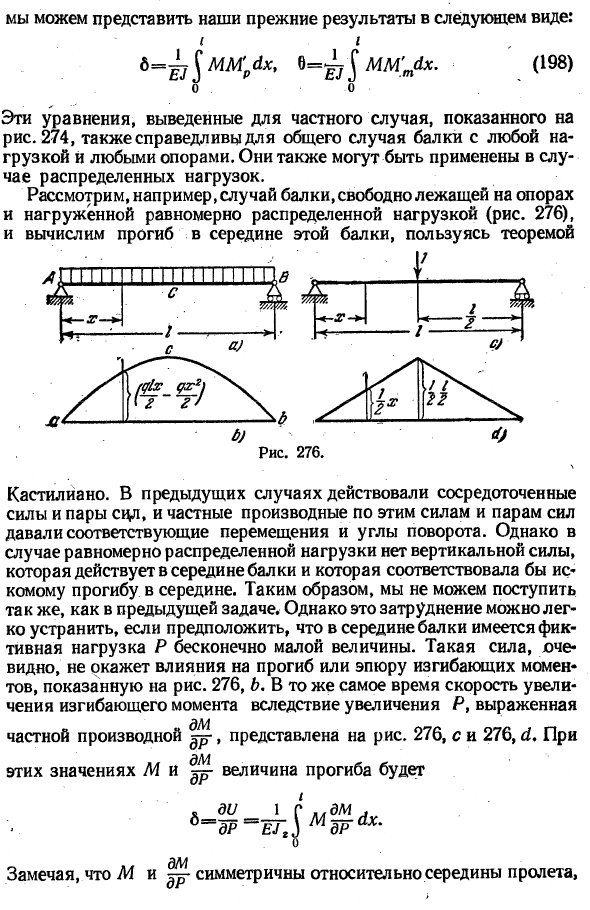
Например, рассмотрим случай балки, которая свободно размещена на опоре и равномерно распределена (рис. 276), и воспользуемся теоремой для вычисления прогиба в центре этой балки Фигура Castigliano. In в предыдущем случае сработали концентрация и пара * * L. А частные разности этих сил и силовых пар давали соответствующие углы смещения и поворота.

Поэтому вы не можете сделать то же самое с предыдущей задачей. Однако если предположить, что в середине балки имеется бесконечно малая мнимая нагрузка Р, то эту трудность можно легко устранить.

Такая сила, очевидно, не влияет на прогиб или диаграмму изгибающего момента, показанную на рисунке 5. 276, b. At в то же время скорость увеличения изгибающего момента обусловлена увеличением Р、 Частные производные показаны на рис. 276, s и 276, а также th.

С этим значением «Ди 1 г ЛАДМ. Б-д-с ^ Пру <1х. обратите внимание, что и и^симметричны относительно центра пролета, поэтому вы получаете следующее: 6 = Если вы хотите вычислить угол поворота кромки балки рис. 276,и помочь с теоремой Кастильяно, необходимо принять ничтожную величину силы, приложенной V. 276. В свою очередь, частные производные представлены рассказчиком. 277, и И 277.6.

Необходимый угол поворота на конце балки равен — »- шггу » Дж… — Вы можете видеть, что результат, полученный с использованием предостерегающей теоремы Кастильяно, совпадает с результатом, полученным ранее(стр. 126). ^Задачи 1.«Мы используем теорему Кастильяно для определения отклонения и угла поворота конца равномерно нагруженной консоли. .. * ’•• 2.

Определить отклонение конца одноконсольной балки, показанной на фиг. 278. Один. ■ ’ .* Рисунок 278. 8.Поддержка горизонтального перемещения•к раме, показанной на фиг. 279, вызванная горизонтальной силой Yu■a  / / l: nt ■Ответ. Б ^ БФ + Ф ’ 1. / * l рисунок 280.. 4.Если размеры стержней AC и BC одинаковы, и их необходимо учитывать, то определяют увеличение расстояния HELL, которое вызвано Rils и(рисунок 280).

Обратите внимание только на изгиб rod. It предполагается, что выход а не очень мал, так что влияние прогиба на величину изгибающего момента может быть незначительным.* л• ’ л- — <- O’rssh * ■b.’| ля■$)-（ \ р, т± ！ 1 1. Ответ is. it это Ота-д—^ -. 5.Определите отклонение на расстоянии от левого края равномерно нагруженной балки, показанное на Рис. 4. ？76, Об.

Решение. Применение бесконечно малых нагрузок Р АСП о расстоянии от левого конца, частичный выпуск может быть найден&в&, 1 В. Это показано на рисунках 281 a и 281 b. используя параболу M Рисунок 281.. Используя схему, показанную на рисунке 276, вы получите программу b% required — Задняя сторона.) подставляя X вместо a и/ — x вместо b, мы можем сопоставить этот результат с полученным ранее уравнением криволинейной оси «салки» (стр. 126).

Смотрите также:

Предмет сопротивление материалов: сопромат 

Деформация ферм	Изгиб, вызываемый ударом
Приложение теоремы Кастилиано к решению статически неопределимых задач	Общее выражение энергии деформации