Оглавление:
Теоретические основы электротехники
Теоретические основы электротехники (ТОЭ ) — техническая дисциплина, связанная с изучением теории электричества и электромагнетизма. ТОЭ подразделяется на две части — теорию электрических цепей и теорию поля. Изучение ТОЭ является обязательным во многих технических ВУЗах, поскольку на знании этой дисциплины строятся все последующие: электротехника, автоматика, энергетика, приборостроение, микроэлектроника, радиотехника и другие.
Электротехника – это наука, исследующая вопросы производства, передачи, распределения и использования электрической энергии.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Введение. Основные методы анализа линейных электрических цепей постоянного тока
План контрольной работы:
- Общие положения и определения. Элементы цепей и их характеристики.
- Режимы работы электрической цепи.
- Законы Кирхгофа.
- Обзор методов анализа цепей постоянного тока.
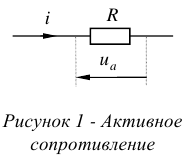
Общие положения и определения. Элементы цепей и их характеристики
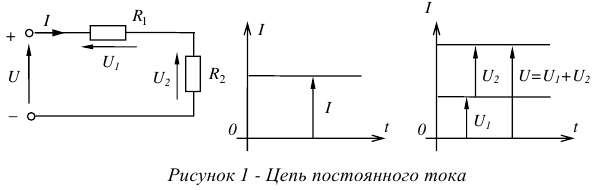
Электрической цепью называется искусственно созданный путь для электрического тока. Пример электрической цепи дан на рисунке 1.
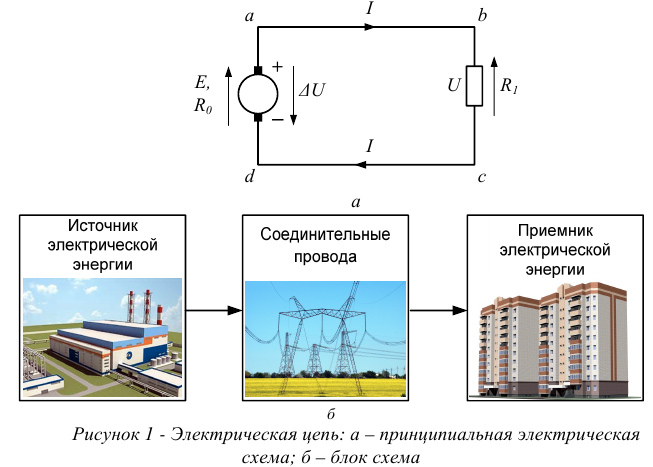
Основное назначение электрической цепи — распределение и взаимное преобразование электрической и других видов энергии.
Электрическая цепь состоит из трех основных элементов:
- источника электрической энергии;
- приемника электрической энергии;
- соединительных проводов.
Рассмотрим каждый из этих элементов цепи подробнее. 1.1.1.1 Источник электрической энергии
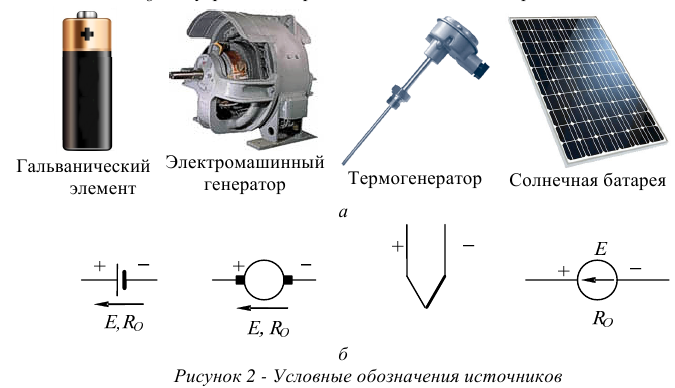
Источники электрической энергии разнообразны: гальванические элементы, аккумуляторы, генераторы, термоэлектрические и солнечные батареи и т.д., рисунок 2,а.
Они превращают химическую, механическую, тепловую, световую или энергию других видов в электрическую энергию.
На схемах источники энергии обозначаются так, как показано на рисунке 2,6.
Везде  — внутреннее сопротивление источника энергии.
— внутреннее сопротивление источника энергии.
В элементах и аккумуляторах, внутреннее сопротивление — это сопротивление электролита и граничных слоев между электролитом и электродами, в генераторах — это сопротивление меди обмоток.
Основное назначение источника энергии — создать и постоянно поддерживать в цепи разность потенциалов, разность электрических уровней; создать как бы электрический напор, под воздействием которого и образуется упорядоченное движение электрических зарядов, то есть ток.
Принято зажим высшего потенциала источника обозначать знаком «+», а зажим низшего потенциала знаком «-».
Разность электрических потенциалов количественно определяется величиной, которая называется — электродвижущей силой или коротко ЭДС и обозначается на схемах буквой « »
»

где  — высший потенциал или уровень источника;
— высший потенциал или уровень источника;  — низший потенциал источника.
— низший потенциал источника.
Направление действия ЭДС обозначается стрелкой, направленной от низшего потенциала к высшему, то есть от «-» к «+».
Работа источника хорошо оценивается с помощью, так называемой внешней характеристики.
Внешней характеристикой называется функциональная зависимость напряжения на клеммах источника от величины тока, протекающего через источник.
Примерный вид внешних характеристик источников электрической энергии показан на рисунках 3 и 4.
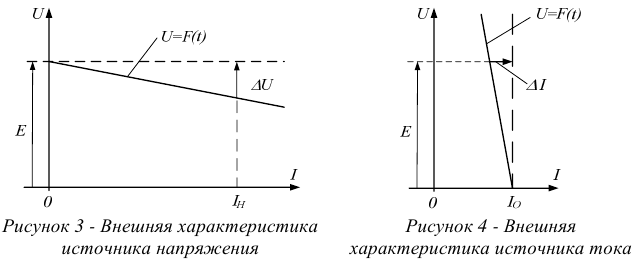
Из характеристики видно, что с увеличением тока напряжение на клеммах источника несколько уменьшается за счет потери напряжения на внутреннем сопротивлении 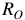 . В целом, же с ростом тока, напряжение на источнике остается более или менее постоянным.
. В целом, же с ростом тока, напряжение на источнике остается более или менее постоянным.
Подобные характеристики имеют гальванические элементы, аккумуляторы, электромашинные генераторы постоянного тока, выпрямители.
На рисунке 4 приведена внешняя характеристика источника электрической энергии другого вида.
Здесь, ток вырабатываемый источником остается более или менее постоянным, при значительном изменении напряжения на клеммах источника.
Отличительная особенность таких источников — очень большая величина внутреннего сопротивления, значительно превышающая сопротивление приемника электрической энергии. Данные источники строят по специальным схемам и широко применяют в современной электронике.
Приемник электрической энергии
Приемники электрической энергии или нагрузки, или потребители -разнообразны. Это могут быть электрические лампы, нагревательные приборы, электродвигатели и другие устройства.
В нагрузках электрическая энергия преобразуется в тепловую, световую, механическую и другие виды энергии.
На схемах, нагрузка учитывается с помощью соответствующих сопротивлений и условно обозначается так, как показано на рисунке 5.

В общем случае сопротивление нагрузки  зависит от тока, протекающего по нему. Однако, эта зависимость при расчетах цепей используется редко.
зависит от тока, протекающего по нему. Однако, эта зависимость при расчетах цепей используется редко.
На практике, чаще используют зависимость напряжения нагрузки от тока нагрузки, которая называется вольтамперной характеристикой.
Вольтамперной характеристикой называется функциональная зависимость напряжения на зажимах нагрузки от тока, протекающего через нагрузку.
Вольтамперные характеристики могут быть самыми разнообразными, например такими, как показано на рисунке 6.
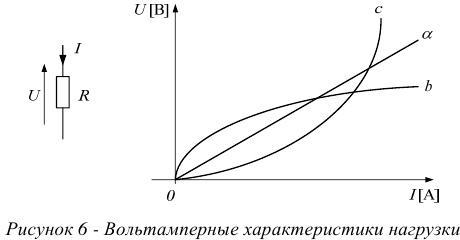
Характеристика  называется линейной. Характеристики
называется линейной. Характеристики  и
и 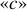 называются нелинейными. Поэтому нагрузки бывают линейными и нелинейными.
называются нелинейными. Поэтому нагрузки бывают линейными и нелинейными.
Линейным элементом или нагрузкой называют такой, сопротивление которого 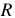 , при любых значениях тока через него, остается постоянным, а вольтамперная характеристика представляет собой прямую линию.
, при любых значениях тока через него, остается постоянным, а вольтамперная характеристика представляет собой прямую линию.
Нелинейным элементом называют такой, сопротивление которого 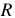 непостоянно и зависит от величины тока, проходящего через него, а вольтамперная характеристика представляет собой кривую линию.
непостоянно и зависит от величины тока, проходящего через него, а вольтамперная характеристика представляет собой кривую линию.
Только линейные элементы подчиняются закону Ома:


Соединительные провода
Соединительные провода или линия, обозначены на рисунке 1 — 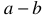 и
и 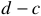 . Они обеспечивают передачу электрической энергии, транспортируют энергию от источника к нагрузке.
. Они обеспечивают передачу электрической энергии, транспортируют энергию от источника к нагрузке.
Их назначение передать электрическую энергию потребителю с минимальными потерями.
Рассмотрев отдельные элементы, вернемся обратно к электрической цепи, как к сосредоточию всех элементов.
Основные определения теории цепей постоянного тока
Цепью постоянного тока называется такая цепь, в которой ЭДС, токи и напряжения остаются постоянными по величине и не зависят от времени.
Цепи делятся на два больших класса:
- линейные;
- нелинейные.
Электрические цепи, содержащие только элементы с линейными вольтамперными характеристиками, называются линейными цепями.
Электрические цепи, содержащие элементы с нелинейными характеристиками называются нелинейными цепями.
Строго говоря, любые цепи нелинейны, однако, если степень нелинейности мала, то ею пренебрегают и считают такую цепь линейной.
В дальнейшем мы будем рассматривать пока только линейные цепи, так как лишь они подчиняются закону Ома и могут рассчитываться аналитическими методами.
Режимы работы электрической цепи
Любая электрическая цепь состоит из двух участков:
- внешний участок цепи, с сопротивлением
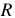 ;
; - внутренний участок цепи, имеющий сопротивление
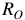 . Внешним участком цепи или внешней цепью называют часть
. Внешним участком цепи или внешней цепью называют часть
цепи, которая присоединяется извне к зажимам источника.
Внутренним участком цепи или внутренней цепью называют часть цепи, которая проходит внутри источника энергии между его зажимами через электролит или обмотки генератора.
Электрические цепи делятся на замкнутые и разомкнутые. Замкнутая цепью — такая, в которой имеется непрерывный путь для тока, а общее сопротивление цепи меньше бесконечности, 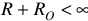 .
.
Разомкнутой цепью называют такую цепь, в которой путь для тока прерывается, а общее сопротивление равно бесконечности 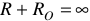 .
.
По закону Ома для полной цепи имеем 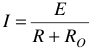 , если
, если 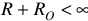 то
то 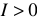 , если
, если 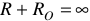 , то
, то 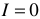 .
.
Отсюда следуют выводы:
- 1) только в замкнутой цепи может протекать ток;
- 2) в разомкнутой цепи ток не существует, но может существовать напряжение или ЭДС.
Ток протекает по проводнику цепи, поэтому стрелку тока принято размечать на самом проводнике.
- За положительное направление тока во внешней цепи, принято направление от высшего потенциала к низшему, то есть от «+» к «-».
- За положительное направление тока во внутренней цепи принято направление от низшего потенциала к высшему, то есть от «-» к «+».
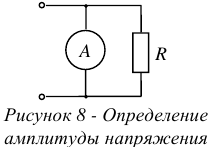
Напряжение на любом участке цепи есть реакция на ток, поэтому стрелку напряжения принято размечать параллельно элементу и всегда против ранее размеченной стрелки тока. (см. рисунок 8).
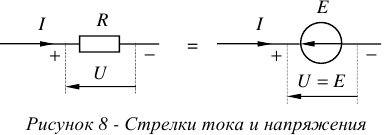
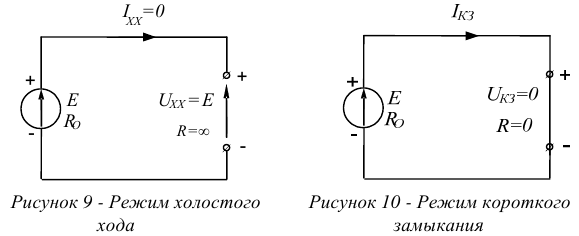
Электрическая цепь может работать в различных режимах, однако все эти режимы, сколько бы их ни было, находятся между двумя крайними режимами — холостым ходом и коротким замыканием.
Режимом холостого хода цепи называют такой режим, при котором сопротивление нагрузки 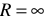 , то есть внешняя цепь разомкнута (см. рисунок 9). Следовательно,
, то есть внешняя цепь разомкнута (см. рисунок 9). Следовательно,

При режиме холостого хода ток холостого хода равен нулю. Режимом короткого замыкания цепи называется такой режим, при котором сопротивление нагрузки 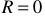 , то есть внешняя цепь замкнута накоротко (см. рисунок 10). Следовательно,
, то есть внешняя цепь замкнута накоротко (см. рисунок 10). Следовательно,
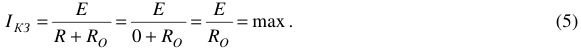
Таким образом, при коротком замыкании ток в цепи максимален и ограничивается только величиной внутреннего сопротивления 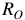 источника энергии.
источника энергии.
Чтобы ток короткого замыкания не разрушал источника его внутреннее сопротивление не должно быть слишком малым.
Если записать уравнения электрического состояния цепи, показанной на рисунке 1, по второму закону Кирхгофа, то получим
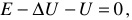
отсюда
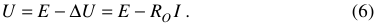
Из выражения (1.5) следует, что

ЭДС источника численно равна напряжению на его клеммах при холостом ходе.
ЭДС источника отличается от напряжения источника на величину потери напряжения внутри источника.
ЭДС — самое большое напряжение, которое может развивать источник при холостом режиме.
Из выражения (5) следует, что внутреннее сопротивление должно быть минимальным, чтобы внутри источника не было больших потерь напряжения.
Из условий (4) и (5) выбирается оптимальное значение величины внутреннего сопротивления 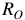 источника.
источника.
Законы Кирхгофа

До сих пор мы рассматривали простые или неразветвленные цепи. Эти цепи решаются с помощью закона Ома. Сложные или разветвленные цепи рассчитываются при помощи законов Кирхгофа.
Законы Кирхгофа являются основными расчетными законами электротехники. Закон Ома частный случай законов Кирхгофа.
Портрет великого немецкого физика Г.Р. Кирхгофа приведен на рисунке 11.
Сложной или разветвленной цепью называют такая, в которой имеется несколько путей для растекания токов (см. рисунок 12).
Точки разветвления цепи А и Б — узлы цепи.
Узлами называются точки цепи, в которых соединяются между собой три или более проводников.
Проводники, соединяющие между собой узлы, называются ветвями.
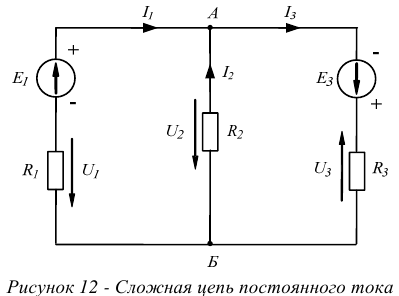
Ветви бывают двух видов: активные и пассивные.
- Активной ветвью называется такая ветвь, которая содержит не только сопротивления, но и источники энергии.
- Пассивной ветвью называется такая ветвь, которая содержит только сопротивления, но не содержит источников энергии.
Таким образом, сложная цепь состоит из узлов и ветвей, то есть из 2-х элементов, поэтому и законов Кирхгофа два. Первый закон Кирхгофа управляет узлами, а второй — ветвями (контурами). Первый закон Кирхгофа гласит:
В любом узле сложной цепи алгебраическая сумма токов равна нулю.

где 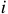 — количество токов связанных с рассматриваемым узлом;
— количество токов связанных с рассматриваемым узлом; 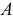 — обозначение рассматриваемого узла.
— обозначение рассматриваемого узла.
Первый закон основан на принципе невозможности накопления электрического заряда в одной точке цепи.
Принято токи, притекающие к узлам цепи, считать положительными и брать со знаком плюс, а токи, оттекающие от узлов, считать отрицательными и брать со знаком минус.
Запишем первый закон Кирхгофа для узлов А и Б нашей цепи (рисунок 1.10).
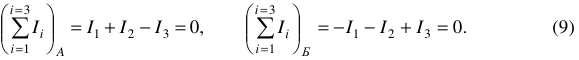
Сравнивая уравнения между собой, видим, что одно из них является следствием другого. Поэтому в цепи выделяют узлы, которые называют независимыми.
Независимыми узлами называют такие, которые отличаются друг от друга, хотя бы одним током.
Число независимых уравнений, составляемых по первому закону Кирхгофа, равно числу независимых узлов в сложной цепи и равно общему числу узлов в цепи без одного.
Число независимых узлов = 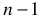 , (10)
, (10)
где 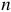 — общее число узлов сложной цепи.
— общее число узлов сложной цепи.
Ветви сложной цепи, образуют контура.
Второй закон Кирхгофа гласит:
В любом контуре сложной цепи алгебраическая сумма ЭДС и напряжений действующих в этом контуре равна нулю.

где 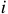 — количество источников ЭДС в рассматриваемом контуре;
— количество источников ЭДС в рассматриваемом контуре; 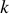 — количество напряжений входящих в данный контур.
— количество напряжений входящих в данный контур.
Данная формулировка справедлива, если стрелки напряжений на схеме цепи расставлены против стрелок токов.
Примечание:
В некоторых литературных источниках, стрелки напряжений направляются согласно стрелкам тока. Это допустимо, если использовать следующую формулировку второго закона Кирхгофа:
В любом контуре сложной цепи, алгебраическая сумма ЭДС всегда равна алгебраической сумме напряжений действующих в этом контуре.

Второй закон Кирхгофа записывается только для независимых контуров.
Независимыми контурами сложной цепи называются такие, которые отличаются друг от друга хотя бы одним элементом цепи не использованным в ранее намеченных контурах.
Число независимых уравнений, составленных по второму закону Кирхгофа, равно числу независимых контуров в цепи.
Число уравнений по 2-му закону Кирхгофа = 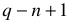 , (13)
, (13)
где ц- общее число ветвей всей цепи.
При обходе по контуру стрелки ЭДС и напряжений, совпадающие с направлением обхода, берутся со знаком плюс, встречно направленные — со знаком минус.
Запишем уравнения электрического состояния контура (см. рисунок 12) по второму закону Кирхгофа:
а) при обходе слева направо 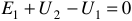 ;
;
б) при обходе справа налево 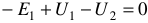 .
.
Следовательно, направление обхода контуров можно выбирать произвольно.
Законы Кирхгофа позволяют рассчитывать самые сложные цепи.
Часто преподаватели задают контрольную работу на нахождение баланса мощностей:
Обзор методов анализа цепей постоянного тока
В настоящее время разработано много методов для расчета цепей постоянного тока. В зависимости от конфигурации и условий заданной цепи для расчета цепи применяются различные методы.
Искусство расчетчика состоит в том, что он находит наиболее рациональный метод решения к конкретно заданной цепи. Сделаем краткий обзор наиболее употребительных методов расчета цепей.
Метод законов Кирхгофа
Это старейший из расчетных методов. Он основан на составлении уравнений по первому и второму законам Кирхгофа и решении их относительно токов текущих в ветвях. Порядок системы уравнений здесь равен количеству неизвестных токов
Непосредственное применение законов Кирхгофа к расчету сложной цепи приводит к весьма громоздким вычислениям, так как приходится решать систему с большим числом уравнений. Поэтому, этот метод на практике применяется крайне редко в виду его неэкономичности.
Метод контурных токов
Метод контурных токов был предложен известным английским физиком и электротехником Джеймсом К. Максвеллом. По этому методу цепь разбивается на ряд контуров, соприкасающихся друг с другом.
Предполагается, на время расчета, что каждый контур обтекается только присущим ему током, который называется контурным током. Контурных токов столько, сколько имеется в цепи независимых контуров. Поскольку, контуров в цепи всегда меньше числа ветвей, то контурных токов в цепи всегда меньше числа реальных токов.
Таким образом, основное преимущество метода контурных токов перед методом законов Кирхгофа состоит в сокращении числа расчетных уравнений.
По известным контурным токам, действительные токи определяются простым алгебраическим сложением.
Метод контурных токов получил широкое распространение в инженерной практике, благодаря экономным затратам времени на расчет.
Метод узловых потенциалов
Метод узловых потенциалов основан на первом законе Кирхгофа и на законе Ома. Преимущество метода состоит в том, что он позволяет сократить число расчетных уравнений и тем самым уменьшить вычислительную работу.
Согласно методу, один из узлов цепи мысленно заземляется, что не влияет на работу цепи. Потенциалы остальных узлов определяются из решения специальной системы уравнений.
Токи в ветвях находят по разности потенциалов между узлами, с учетом межузлового сопротивления.
Поскольку узлов в цепи всегда меньше, чем ветвей, метод весьма экономичен.
Метод узлового напряжения
Это частный случай метода узловых потенциалов для цепи с двумя узлами.
Чтобы токи в ветвях были рассчитаны правильно, необходимо с большой точностью находить величину узлового напряжения. В этом один из крупных недостатков метода узлового напряжения.
Указанный метод получил весьма широкое применение в расчетной практике благодаря своей экономичности в вычислительной работе.
Метод наложения (суперпозиции)
Метод основан на принципе Д’Аламбера — независимости действия сил на линейную систему. Проиллюстрируем принцип Д’Аламбера, рисунком 14.
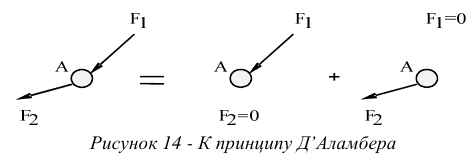
В электрической цепи вместо сил используют ЭДС цепи. Схему решают столько раз, сколько имеется в цепи источников энергии. Результаты решения алгебраически суммируют.
Метод линейных преобразований
Данный метод основан на использовании закона Ома и формул последовательного, параллельного, смешанного соединения сопротивлений, а также перехода от соединения сопротивлений в треугольник к звезде.
Сначала сложная цепь свертывается до предельно простой и решается по закону Ома — прямой путь. Затем, полученное решение развертывается до заданной конфигурации цепи — обратный путь.
Основное условие применимости метода — в цепи должен быть только один источник питания.
Метод эквивалентного генератора
Метод эквивалентного генератора позволяет определить ток в одной отдельно взятой ветви сложной цепи с сопротивлением 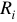 , без расчета всех остальных токов.
, без расчета всех остальных токов.
Суть метода в том, что всю внешнюю по отношению к искомой ветви цепь представляют, как некий эквивалентный генератор с напряжением на зажимах 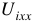 и некоторым внутренним сопротивлением
и некоторым внутренним сопротивлением 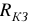 .
.
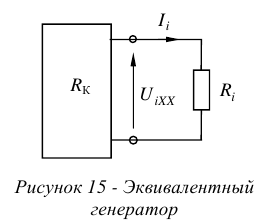
Эквивалентная схема цепи, полученная в результате преобразований исходной схемы, изображена на рисунке 15.
В результате, искомый ток определяют по закону Ома
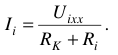
Нелинейные цепи постоянного тока
План контрольной работы:
- Нелинейные цепи (общие понятия).
- Графоаналитический метод расчета нелинейных цепей.
- Графический метод расчета нелинейных цепей.
- Аналитические расчеты нелинейных цепей.
Нелинейные цепи общие положения и определения
Электрические цепи, содержащие элементы с нелинейными вольтамперными характеристиками, называются нелинейными.
Нелинейные элементы делятся на симметричные и несимметричные.
Симметричными нелинейными элементами называются такие, у которых вольтамперные характеристики не зависят от направления тока в них и напряжения на зажимах.
Сюда можно отнести, например, электрические лампы, варисторы, термисторы, катушки со стальными сердечниками.
Несимметричными нелинейными элементами называются такие, у которых вольтамперные характеристики различны при разных направлениях тока и напряжения на зажимах.
Сюда можно отнести, например, электрическую дугу с разнородными электродами, полупроводниковые приборы (диоды, транзисторы, тиристоры).
Часто преподаватели задают контрольные работы на расчёт нелинейных цепей:
- Графоаналитический метод расчета нелинейных цепей
- Графический метод расчета неразветвленных цепей с нелинейными элементами
- Параллельное соединение элементов электрической цепи
- Расчёт смешанного соединения элементов электрической цепи
- Аналитический расчет нелинейных цепей
Цепи однофазного переменного синусоидального тока. Общие положения и определения
План контрольной работы:
- Общие положения и определения. Источники синусоидальных ЭДС и токов.
- Причины выбора синусоидальной формы тока и промышленной частоты.
- Действующие и средние значения периодических ЭДС, напряжений и токов.
- Векторные диаграммы.
- Изображение синусоидальных функций времени комплексными числами (символический метод).
Общие положения и определения. Источники синусоидальных ЭДС и токов
До сих пор мы изучали электрические цепи постоянного тока, в которых токи и напряжения зависят только от сопротивлений и не зависят от времени. Пример подобной цепи приведен на рисунке 1.
Теория переменных токов изучает электрические цепи, в которых токи и напряжения зависят и от величин сопротивлений и от времени. Пример такой цепи показан на рисунке 2.
Из огромного многообразия переменных токов, в промышленности, получили применение переменные синусоидальные токи.
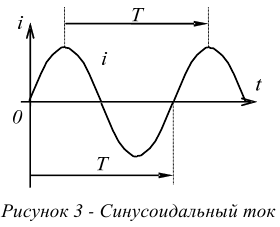
Синусоидальным током называется такой ток, величина и направление которого изменяется в зависимости от времени по закону синуса.
Время 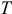 , в течение которого синусоида претерпевает полный цикл своего изменения называется периодом, см. рисунок 3.
, в течение которого синусоида претерпевает полный цикл своего изменения называется периодом, см. рисунок 3.
Размерность периода — 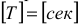 .
.
Число периодов в секунду определяет частоту переменного тока — 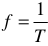 . Частота измеряется в герцах —
. Частота измеряется в герцах — 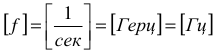 . За один герц принимается частота тока в один период в одну секунду.
. За один герц принимается частота тока в один период в одну секунду.
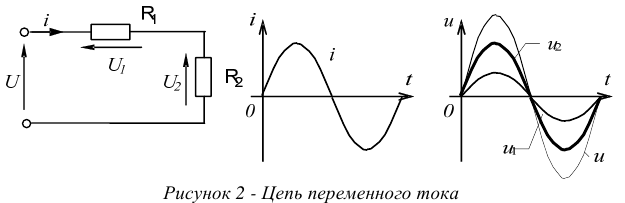
Переменный синусоидальный ток вырабатывается в особых машинах, которые называются генераторами переменного тока. Эти генераторы работают на принципе закона электромагнитной индукции. Упрощенная схема такой машины приведена на рисунке 4, а. Там же, рисунок 4,6, показан общий вид генераторов на электростанции.
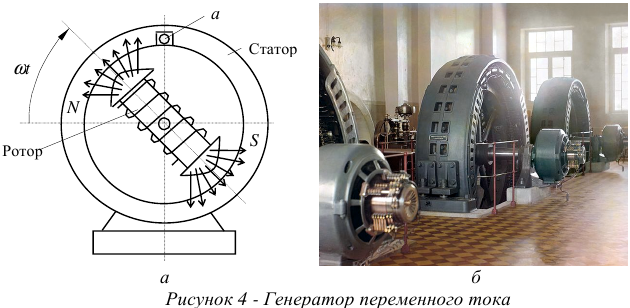
Генератор состоит из неподвижного статора, на внутренней поверхности которого в особых пазах уложена обмотка. Обмотка статора на рисунке показана в виде одного витка — 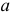 . Внутри статора помещается ротор, приводимый во вращение извне каким либо двигателем (например: паровой или гидротурбиной; двигателем внутреннего сгорания).
. Внутри статора помещается ротор, приводимый во вращение извне каким либо двигателем (например: паровой или гидротурбиной; двигателем внутреннего сгорания).
Ротор представляет собой мощный электромагнит постоянного тока. Магнитное поле ротора, пересекая при вращении витки обмотки статора, наводит в ней синусоидальную ЭДС. Действительно, при вращении ротора, индукция магнитного поля в обмотке изменяется по синусоидальному закону

где 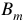 — амплитуда индукции поля в обмотке статора;
— амплитуда индукции поля в обмотке статора; 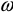 — угловая частота вращения ротора генератора.
— угловая частота вращения ротора генератора.

где 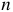 — число оборотов ротора генератора в минуту;
— число оборотов ротора генератора в минуту;
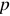 — число пар полюсов магнитного полюса ротора генератора. Для генератора, показанного на рисунке 3.4,
— число пар полюсов магнитного полюса ротора генератора. Для генератора, показанного на рисунке 3.4, 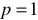 .
.
ЭДС индуктируемая в проводнике обмотки статора определяется известным выражением
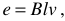
откуда
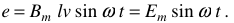
Причины выбора синусоидальной формы тока и промышленной частоты
В разных странах частота переменного тока стандартизована и несколько различна. Например, в европейских странах, в России частота 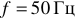 , в США, Японии и ряде других стран
, в США, Японии и ряде других стран 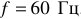 .
.
Величина промышленной частоты выбрана по многим соображениям, главные из них:
- 1) отсутствие вредного действия на глаза человека мигания источников электрического освещения;
- 2) оптимальность габаритов электрических машин и аппаратов;
- 3) минимум потерь энергии на гистерезис и вихревые токи в сердечниках машин и аппаратов.
Примечание:
1) вес и габариты электрических машин обратно пропорциональны частоте питающего тока;
2) потери энергии на вихревые токи — 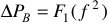 , а потери энергии на гистерезис —
, а потери энергии на гистерезис — 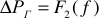 .
.
В России угловая частота промышленного переменного тока равна:

Период промышленного переменного синусоидального тока

Частота постоянного тока равна нулю. Поэтому постоянный ток есть частный случай переменного тока, частота которого равна нулю, а период равен бесконечности.
Все генераторы переменного тока вырабатывают синусоидальные токи. Синусоидальность выбрана по многим причинам, главные из них:
1)из всех периодических кривых синусоида самая плавная (ее производная — также синусоидальная величина), последнее обеспечивает отсутствие динамических толчков при работе машин и перенапряжений в изоляции обмоток;
2) только синусоидальная форма токов дает вращающееся магнитное поле, что обеспечивает простое устройство двигателей переменного тока;
3) синусоида относительно просто записывается математически.
В общем случае синусоидальный ток может иметь вид, показанный на рисунке 5.
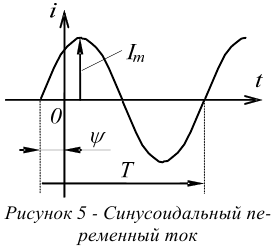
Мгновенное значение переменного тока можно записать в форме:
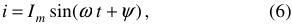
где 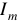 — амплитуда синусоиды, амплитудой называют наибольшее мгновенное значение;
— амплитуда синусоиды, амплитудой называют наибольшее мгновенное значение;
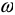 — угловая частота в рад/сек;
— угловая частота в рад/сек; 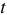 — время в сек;
— время в сек;
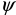 — начальная фаза или фаза включения. Она показывает, какое мгновенное значение синусоидальной величины имеет место в момент включения;
— начальная фаза или фаза включения. Она показывает, какое мгновенное значение синусоидальной величины имеет место в момент включения; 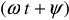 — аргумент синусоиды.
— аргумент синусоиды.
Таким образом, синусоида выражается через амплитуду и аргумент.
Действующее и среднее значения периодических ЭДС, напряжений и токов
Действующее значение периодических ЭДС, напряжений и токов
Переменный ток изменяется настолько быстро, что инертные измерительные приборы и электрические машины не успевают следовать за его мгновенными изменениями. Они улавливают некоторое усредненное значение переменного тока.
Поэтому обычно переменный ток сравнивают по действию с постоянным током. Отыскивают переменному току некоторый эквивалент в виде постоянного тока. Этот постоянный ток и называется действующим значением переменного тока.
Сравним переменный ток с постоянным током по количеству выделяемого тепла на одном и том же сопротивлении.
Рисунок 6 иллюстрирует вывод нижеследующих формул.
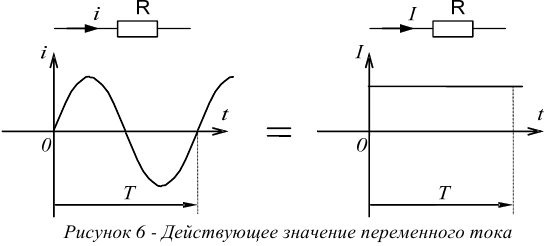
Количество тепла, выделяемое на сопротивлении 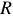 за время
за время 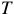 , переменным током
, переменным током 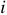 определяется так
определяется так

Количество тепла, выделяемое на сопротивлении 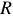 за время
за время 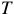 , постоянным током
, постоянным током 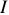 определяется так
определяется так

Постоянный ток 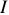 будет являться действующим значением переменного тока
будет являться действующим значением переменного тока 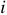 , если их тепловое действие будет одинаково. Приравнивая выражения (7) и (8) получаем
, если их тепловое действие будет одинаково. Приравнивая выражения (7) и (8) получаем
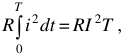
откуда выражая значение 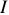 , окончательно имеем
, окончательно имеем

Действующим значением переменного тока называется такой постоянный ток, который на том же сопротивлении и за то же время выделяет столько же тепла, что и данный переменный ток.
Обычно, время интегрирования 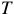 , принимают равным периоду переменного тока, поэтому действующее значение переменного тока равно среднеквадратичному значению его мгновенной величины.
, принимают равным периоду переменного тока, поэтому действующее значение переменного тока равно среднеквадратичному значению его мгновенной величины.
Для напряжения, действующее значение будет равно:

Выражения (9) и (10) позволяют найти действующие значения переменного тока или напряжения изменяющихся по кривой любой формы.
Определим действующее значение для синусоидального переменного тока.
Пусть 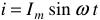 . Тогда, согласно (9) имеем
. Тогда, согласно (9) имеем
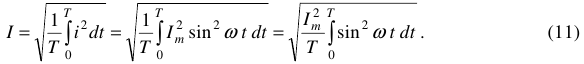
Интеграл под знаком корня возьмем отдельно.
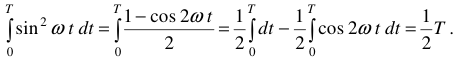
Подставляя последнее значение в выражение (11), получим
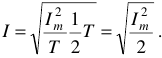
Отсюда имеем действующие значения переменного тока и напряжения:

Или амплитуды тока и напряжения:

Электрические машины, аппараты, измерительные приборы работают на действующих значениях. Рассмотрим два примера.
Контрольная работа №1
В цепи, см. рисунок 7, протекает ток, мгновенное значение которого равно 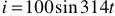 . Найти показания амперметра.
. Найти показания амперметра.
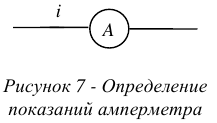
Решение:
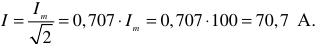
Контрольная работа №2
В цепи, см. рисунок 8, показание вольтметра 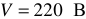 . Какое напряжение действует на изоляцию проводов?
. Какое напряжение действует на изоляцию проводов?
Решение:
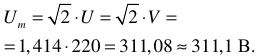
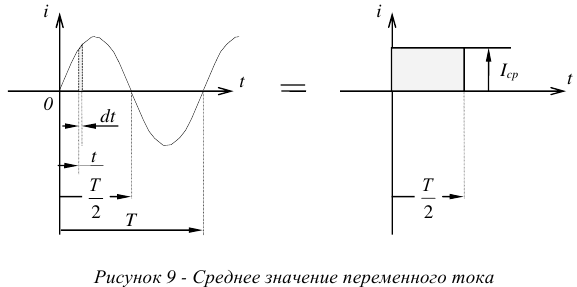
Среднее значение синусоидального переменного тока
Для некоторых расчетов в электротехнике необходимо знать среднее значение переменного тока.
Средним значением переменного тока называется такой переменный ток, произведение которого на интервал времени, равен интегралу данного переменного тока за тот же интервал времени.
Вывод нижеследующих формул иллюстрируется рисунком 9.

Выражение (14) — среднее значение синусоидальной величины за полпериода. Если 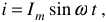 то:
то:
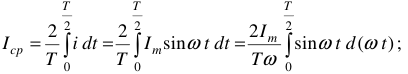
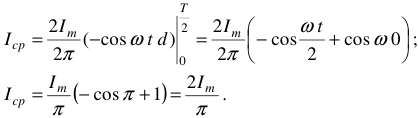
Окончательно имеем:

Часто, для того, чтобы характеризовать форму кривой и легко переходить от среднего значения к действительному, вводят коэффициент формы кривой — 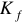 .
.
Коэффициентом формы кривой называют отношение действующего значения к среднему.

Для синусоидальной величины имеем,

Для треугольной формы кривой, 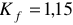 .
.
Для прямоугольной формы (меандра), 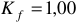 .
.
Векторные диаграммы
Способ анализа цепей синусоидального переменного тока основанный на представлении синусоиды равномерно вращающимся вектором называется — методом векторных диаграмм.
Предположим, что мы имеем равномерно вращающийся вектор, длина которого равна амплитуде синусоиды, а скорость вращения против стрелки часов, равна 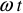 , см. рисунок 10.
, см. рисунок 10.
Первоначальное положение вектора определяется углом у/, который называется начальной фазой.
Тогда проекция данного вектора на ось у может быть записана таким образом

Таким образом, каждой синусоидальной величине можно поставить в соответствие свой вращающийся вектор.
При действиях с несколькими синусоидами получаем несколько векторов, действия над которыми заменяют действия над синусоидальными токами или напряжениями.
Векторы — амплитуды вращаются с одной скоростью, так как частота всех токов и напряжений одна, а значит, относительно друг друга они неподвижны.
Поэтому, когда диаграммы используются для сложения действующих величин напряжений и токов то векторы не вращают.
Векторные диаграммы бывают двух видов:
- лучевые;
- топографические.
Лучевой диаграммой называется такая, в которой все векторы напряжений и токов цепи строят из одной точки.
Топографической диаграммой называется такая, на которой векторы напряжений пристраиваются друг к другу в том же порядке, в котором они действуют в электрической цепи.
Лучевые диаграммы на практике используются редко. Топографические диаграммы применяются очень широко, потому, что они позволяют определять напряжения между любыми точками и узлами электрической цепи.
Векторной диаграммой называется совокупность векторов, характеризующих процесс в электрической цепи.
Способ векторных диаграмм благодаря своей наглядности широко используется на практике.
Изображение синусоидальных функций времени комплексными числами (символический метод)
Инженерный метод расчета электрических цепей переменного тока, основанный на применении комплексных чисел, называется символическим методом.
Этот метод предложил в 1892 г. американский ученый немецкого происхождения Чарлз Протеус Штейнмец. В нем гармонично сочетались выдающиеся качества математика, ученого-электротехника, инженера и изобретателя. Он был шеф-электриком крупнейшего американского электротехнического концерна — фирмы «Дженерал Электрик Компани» (GEC), и его по праву называли «самым крупным оборудованием» фирмы.
Символический метод основан на замене геометрического сложения векторов, сложением алгебраическим комплексных чисел, изображающих эти вектора.

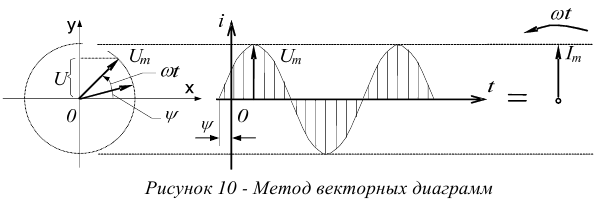
Согласно данному методу, вектора, отображающие синусоидальные токи или напряжения строятся в комплексной плоскости, рисунок 11.
Для удобства построения векторных диаграмм в электротехнике комплексная плоскость поворачивается в положительную сторону на угол 90°, как показано на рисунке 12.
Комплексное число это самый общий вид числа, все остальные числа являются частными случаями этого числа.
Комплексные числа существуют на комплексной плоскости. Комплексной плоскостью называется плоскость, ориентированная относительно двух взаимно перпендикулярных осей, см. рисунок 11.
Вертикальная ось называется осью мнимых чисел. На этой оси лежат все чисто мнимые числа.
Горизонтальная ось называется осью действительных чисел. На ней лежат все действительные числа.
Комплексные числа лежат между осями и имеют проекции и на действительную и на мнимую оси, как показано на рисунке 11.
Комплексным числом называют такое число, которое на комплексной плоскости определяется системой из двух чисел.
Комплексное число позволяет описать вектор его проекциями на оси комплексной плоскости.
Комплексное число может быть представлено в трех формах: алгебраической, тригонометрической и показательной.
Алгебраическая форма

где 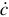 — комплексное число. Оно обозначается точкой над символом;
— комплексное число. Оно обозначается точкой над символом; 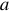 — действительная часть комплексного числа;
— действительная часть комплексного числа; 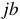 — мнимая часть комплексного числа.
— мнимая часть комплексного числа.
Величина 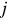 — называется мнимой единицей или оператором поворота на 90° в положительную сторону. Справедливы соотношения:
— называется мнимой единицей или оператором поворота на 90° в положительную сторону. Справедливы соотношения:

Тригонометрическая форма
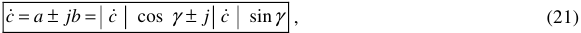
где 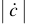 — модуль комплексного числа
— модуль комплексного числа 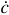 ;
; 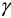 — аргумент комплексного числа
— аргумент комплексного числа 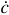 .
.
Модуль комплексного числа  , определяется таким образом
, определяется таким образом

Аргумент комплексного числа — 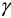 , можно найти по выражению:
, можно найти по выражению:

Справедливы так же соотношения:

Показательная форма
Известно, что 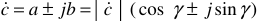 , но согласно формуле Эйлера:
, но согласно формуле Эйлера: 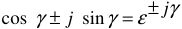 , где
, где 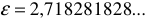 — основание натуральных логарифмов.
— основание натуральных логарифмов.
Поэтому можно записать комплексное число в следующей форме:

Выражение (25) называется показательной формой записи комплексного числа.
Законы Ома и Кирхгофа в комплексной форме
При использовании комплексных чисел, все законы и методы расчета по форме не изменяются, но записываются в комплексном виде: Закон Ома в символической форме:

Первый закон Кирхгофа в символической форме

Второй закон Кирхгофа в символической форме

Основным преимуществом символического метода является то, что геометрические действия над векторами заменяются алгебраическими действиями над комплексами, изображающими эти вектора.
Идеализированные линейные элементы однофазных цепей синусоидального тока
План контрольной работы:
- Идеальный активный элемент.
- Идеальный индуктивный элемент.
- Идеальный емкостный элемент.
Идеальный активный элемент
Активное сопротивление в электрических схемах условно обозначается так, как показано на рисунке I.
Идеальным активным сопротивлением R называется элемент цепи, в котором электрическая энергия преобразуется в тепловую энергию или полезную механическую работу. Идеальный активный элемент не имеет ни магнитных, ни электрических полей. Поэтому он не запасает внутри себя энергию.
Если по активному сопротивлению протекает синусоидальный переменный ток 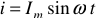 , то напряжение на нем будет
, то напряжение на нем будет

где 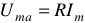 — амплитуда активного напряжения.
— амплитуда активного напряжения.
Графики колебаний тока и напряжения на активном элементе и векторная диаграмма, характеризующая данный элемент приведены на рисунке 2.
На идеальном активном элементе в любой момент времени напряжение, и ток совпадают по фазе, сдвиг фаз между ними равен нулю.
Мощность, потребляемая активным элементом от источника энергии, определится:
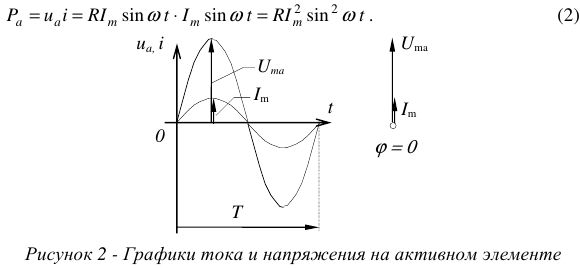
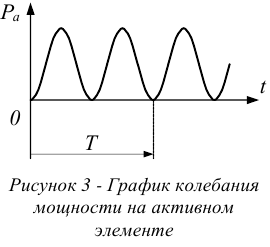
Данное выражение определяет закон колебания мощности на активном элементе цепи. Активная мощность всегда положительна. График, иллюстрирующий выражение (2) показан на рисунке 3.
С энергетической точки зрения, положительная мощность, это мощность, которая поступает из генератора в нагрузку, а отрицательная — та, которая возвращается обратно в генератор. В активном сопротивлении транспорт энергии односторонний. Односторонний транспорт энергии обеспечивает самую большую пропускную способность проводов электрических линий, следовательно, самый экономичный способ их использования. Активный режим является самым энергетически выгодным и экономичным режимом работы цепи.
Идеальный индуктивный элемент
Индуктивность в электрических схемах условно обозначается так, как показано на рисунке 4.
Идеальной индуктивностью 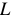 , называют элемент цепи, в котором электрическая энергия полностью преобразуется в энергию магнитного поля. Идеальный индуктивный элемент не имеет нагрева и электрических полей.
, называют элемент цепи, в котором электрическая энергия полностью преобразуется в энергию магнитного поля. Идеальный индуктивный элемент не имеет нагрева и электрических полей.
Индуктивность препятствует всякому изменению тока в цепи. Если по индуктивности протекает синусоидальный переменный ток 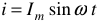 , то напряжение на ней будет:
, то напряжение на ней будет:
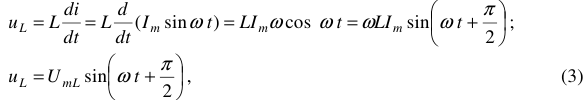
где 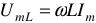 — амплитуда напряжения на индуктивном элементе.
— амплитуда напряжения на индуктивном элементе.
Графики колебаний тока и напряжения на индуктивности и векторная диаграмма, характеризующая данный элемент приведены на рисунке 5.
На идеальном индуктивном элементе в любой момент времени ток отстает от напряжения на угол 90°. Таким образом, здесь мы наблюдаем сдвиг между напряжением и током на угол 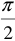 .
.
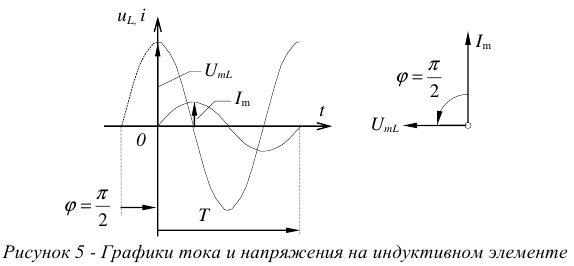
Данный элемент запасает внутри себя энергию в виде магнитного поля. Энергия элемента определяется током, поэтому ток и отстает по фазе. В общем случае, в цепи переменного тока всегда отстает по фазе та величина, которая связана с энергией. На векторной диаграмме, та величина, которая встречается первой, при обходе против часовой стрелки, считается отстающей.
Мощность, потребляемая индуктивным элементом от источника энергии, определится:
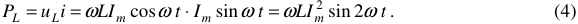
Данное выражение определяет закон колебания мощности на индуктивном элементе цепи. График, иллюстрирующий выражение (4.4) показан на рисунке 6.
Из графика следует, что на идеализированной индуктивности мощность колеблется с удвоенной частотой. При этом мощность принимает как положительные, так и отрицательные значения.
За период изменения тока в цепи, поступление и возврат энергии в индуктивный элемент равны друг другу. Это значит, что, сколько энергии поступает в нагрузку, столько же и возвращается обратно в генератор.
Энергия здесь не тратится, она колеблется между генератором и нагрузкой, бесполезно загружая провода. Здесь существуют встречные потоки энергии, фактическое сечение проводов становится меньше геометрического, в результате пропускная способность линии снижается. В сильноточных непях это вредный режим и от него приходится всеми средствами избавляться.
Идеальный емкостный элемент
Емкость (конденсатор) в электрических схемах условно обозначается так, как показано на рисунке 7.
Идеальной емкостью  , называют элемент цепи, в котором электрическая энергия полностью преобразуется в энергию электрического поля. Идеальный емкостный элемент не имеет нагрева и магнитных полей.
, называют элемент цепи, в котором электрическая энергия полностью преобразуется в энергию электрического поля. Идеальный емкостный элемент не имеет нагрева и магнитных полей.
Емкость препятствует всякому изменению напряжения в цепи.
Ток через емкость — это особый ток, поскольку он проходит по диэлектрику. Это так называемый ток смещения. Он определяется по закону Ома для диэлектрика:

Если по емкости протекает синусоидальный переменный ток 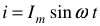 , то напряжение на ней будет
, то напряжение на ней будет
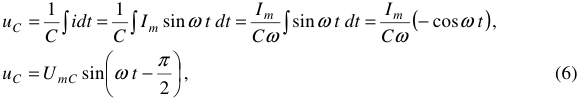
где 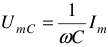 —
—
амплитуда напряжения на емкостном элементе.
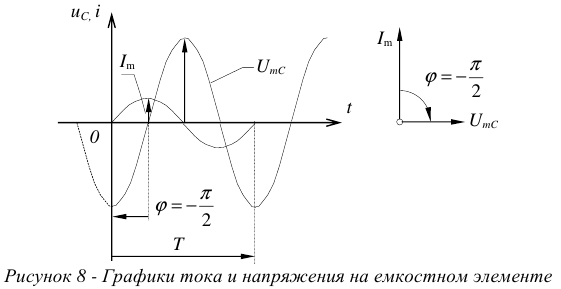
Графики колебаний тока и напряжения на емкости и векторная диаграмма, характеризующая данный элемент приведены на рисунке 8.
На идеальном емкостном элементе в любой момент времени напряжение отстает от тока на угол 90°. Таким образом, здесь мы наблюдаем сдвиг между напряжением и током на угол 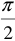 .
.
Данный элемент запасает внутри себя энергию в виде электрического поля.
Энергия элемента определяется напряжением, поэтому напряжение и отстает по фазе.
Мощность, потребляемая емкостным элементом от источника энергии, определится:
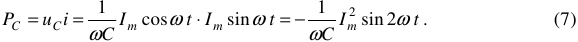
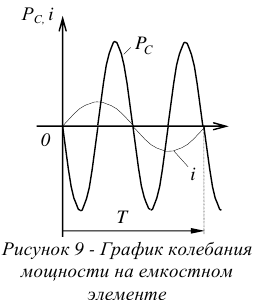
Данное выражение определяет закон колебания мощности на емкостном элементе цепи. График, иллюстрирующий выражение (7) показан на рисунке 9.
Из графика следует, что на идеализированной емкости мощность колеблется с удвоенной частотой. При этом мощность принимает как положительные, так и отрицательные значения.
За период изменения тока, поступление и возврат энергии в емкостном элементе равны друг другу. Это значит, что, сколько энергии поступает в нагрузку, столько же и возвращается обратно в генератор. Энергия здесь, как и в случае с индуктивностью, не тратится, она колеблется между генератором и нагрузкой, бесполезно загружая провода. Встречные потоки энергии приводят к снижению фактического сечения проводов, в результате пропускная способность линии снижается.
Реактивная энергия на емкости противоположна по знаку реактивной энергии на индуктивности. Это означает, что емкость и индуктивность стремятся поглотить друг друга, скомпенсировать друг друга. Такая компенсация широко используется на практике, в частности для организации резонансных режимов.
Полная цепь переменного тока. Мощность в цепи переменного тока
План контрольной работы:
- Закон Ома для полной цепи переменного тока, треугольник напряжений.
- Треугольник сопротивлений и токов.
- Мощность в цепи переменного тока.
Часто преподаватели задают контрольные работы на закон ома, на сопротивление и мощность цепи:
- Закон Ома для полной цепи переменного тока
- Треугольники сопротивлений и тока
- Мощность в цепи переменного тока
Электрические резонансы
План контрольной работы:
- Общая характеристика резонансных цепей.
- Резонанс напряжений. Собственная частота цепи и способы ее регулирования. Волновое сопротивление и добротность контура. Избирательность и полоса пропускания. Частотные характеристики резонанса напряжений. Векторная диаграмма резонанса напряжений.
- Резонанс токов. Собственная частота цепи при резонансе токов. Частотные характеристики резонанса токов. Векторная диаграмма резонанса токов.
Общая характеристика резонансных цепей
Резонансные явления широко используются в технике. Известны резонансы: механические; химические; ядерные; электрические и др.
Режим резонанса наступает лишь тогда, когда частота внешних воздействий на систему равна собственной частоте системы, рисунок 1.
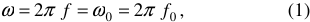
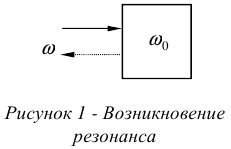
где 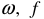 — угловая и временная частота внешних воздействий;
— угловая и временная частота внешних воздействий; 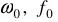 — угловая и временная собственная частота системы.
— угловая и временная собственная частота системы.
Собственной частотой системы называется число переливаний энергии внутри системы из одной формы в другую за одну секунду.
В электрических цепях энергия может сосредотачиваться в разных формах в двух элементах цепи: индуктивном (магнитное поле) и в емкостном (электрическое поле).
Таким образом, электрическая цепь обладает собственной частотой 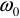 , если в ней имеется хотя бы одна катушка и один конденсатор.
, если в ней имеется хотя бы одна катушка и один конденсатор.
Катушка и конденсатор могут соединяться друг с другом только двумя способами:
- 1) последовательно;
- 2) параллельно.
В связи с этим имеется лишь два вида электрических резонансов: резонанс напряжений и резонанс токов.
Электрические резонансы сопровождаются резким увеличением напряжения или тока, т.е. являются усилительными электрических величин.
Любая пассивная электрическая цепь, находящаяся в режиме резонанса, характеризуется следующими свойствами:
1) входное реактивное сопротивление (для резонанса напряжений) или входная реактивная проводимость цепи (для резонанса токов) равны нулю

2) входное напряжение и ток совпадают по фазе

3) входная мощность чисто активная

Рассмотрим теперь каждый из резонансных режимов в отдельности.
Часто преподаватели задают контрольные работы на резонанс:
Трехфазные электрические цепи с симметричными и несимметричными приемниками
План контрольной работы:
- Понятие о трехфазных источниках ЭДС и тока. Способы получения трехфазного тока. Преимущества трехфазной системы электроснабжения. Способы записи комплексных напряжений генератора.
- Соединение «звездой». Соотношения между токами и напряжениями. Симметричный и несимметричный режимы работы. Роль нулевого провода. Векторные диаграммы.
- Соединение «треугольником». Соотношения между токами и напряжениями. Симметричный и несимметричный режимы работы. Векторные диаграммы.
- Мощность в трехфазной сети. Универсальная формула мощности.
Понятие о трехфазных источниках ЭДС и тока. Способы получения трехфазного тока. Преимущества трехфазной системы электроснабжения. Способы записи комплексных напряжений генератора
Трехфазные системы в настоящее время получили наибольшее распространение. На трехфазном токе работают все крупные электростанции и потребители, что связано с рядом преимуществ трехфазных цепей перед однофазными, важнейшими из которых являются:
- экономичность передачи электроэнергии на большие расстояния;
- возможность применения самого надежного и экономичного, удовлетворяющего требованиям промышленного электропривода, трехфазного асинхронного двигателя с короткозамкнутым ротором;
- возможность получения с помощью неподвижных обмоток вращающегося магнитного поля, на чем основана работа синхронного и асинхронного двигателей, а также ряда других электротехнических устройств.
- уравновешенность симметричных трехфазных систем, это означает, что суммарная мгновенная мощность всех фаз остается величиной постоянной в течение всего периода синусоидальной ЭДС. Уравновешенность имеет важнейшее практическое значение. Если бы суммарная мгновенная мощность пульсировала, то на валу между турбиной и генератором действовал бы пульсирующий момент. Такая переменная механическая нагрузка вредно отражалась бы на генерирующей установке, сокращая срок ее службы.
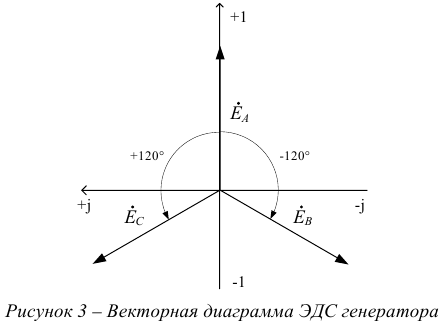
Трехфазной электрической цепью или трехфазной системой цепей называют такую систему, в которой действуют три синусоидальные ЭДС, одинаковой частоты и амплитуды, сдвинутые друг относительно друга по фазе на угол 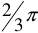 (120°) и создаваемые общим источником энергии. Этим
(120°) и создаваемые общим источником энергии. Этим
источником является трехфазный синхронный генератор.
Он состоит из неподвижной части — статора 1 и подвижной части — ротора 3, рисунок 1.
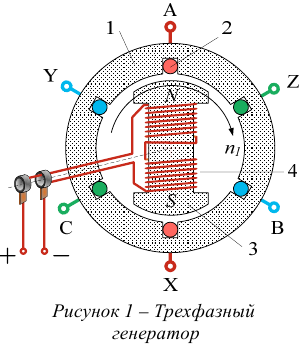
Статор представляет собой пустотелый цилиндр, собранный из листов электротехнической стали, изолированных друг от друга. На внутренней поверхности цилиндра выштампованы канавки — пазы. В пазы статора укладываются три одинаковых обмотки 2, оси которых смещены друг относительно друга на треть окружности статора (на 120°).
Ротор представляет собой электромагнит, обмотка 4 которого, питается постоянным током. Он называется — ток возбуждения. Постоянный ток возбуждения подводится к обмоткам электромагнитов ротора через два изолированных друг от друга и от вала машины кольца, через щетки, скользящие по кольцам. При вращении ротора (магнитного поля) в каждой фазе (обмотке) статора (выводы 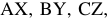 соответственно) по закону электромагнитной индукции будут наводиться ЭДС, изменяющиеся по синусоиде и сдвинутые на 120°. Обмотки генератора и их ЭДС показаны на рисунке 2.
соответственно) по закону электромагнитной индукции будут наводиться ЭДС, изменяющиеся по синусоиде и сдвинутые на 120°. Обмотки генератора и их ЭДС показаны на рисунке 2.
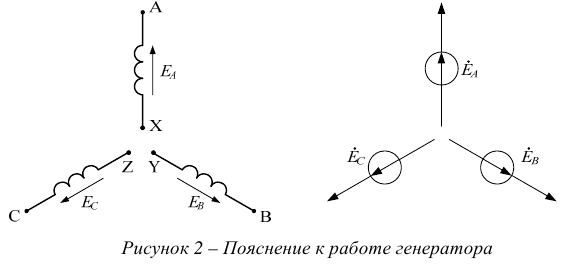
Векторная диаграмма ЭДС генератора показана на рисунке 3.
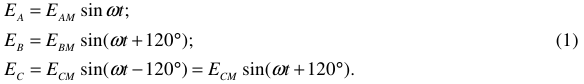
Частота тока в фазах обмотки статора запишется:

где 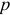 — число пар полюсов обмотки ротора генератора;
— число пар полюсов обмотки ротора генератора; 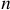 — частота вращения вала.
— частота вращения вала.
Комплексные действующие ЭДС будут иметь выражения:
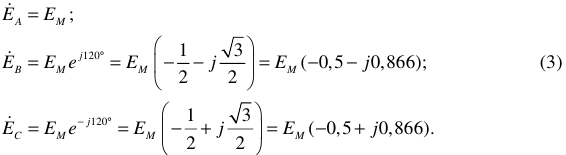
Часть трехфазной системы, в которой может протекать один из ее токов, называется фазой. В каждой фазе следует различать начало и конец.
Началом называются выводы обмотки с высоким потенциалом, а концом — с низким потенциалом.
Таким образом, понятие «фаза» имеет в электротехнике два различных значения:
- фаза как аргумент синусоидально изменяющейся величины;
- фаза как составная часть многофазной электрической системы.
Обмотки трехфазных генераторов, как правило, соединяются по схеме «звезда» (рисунок 4). Соединением в «звезду» называется такое, при котором три начала или три конца фаз соединяются в общую точку, называемую нулевой или нейтральной.
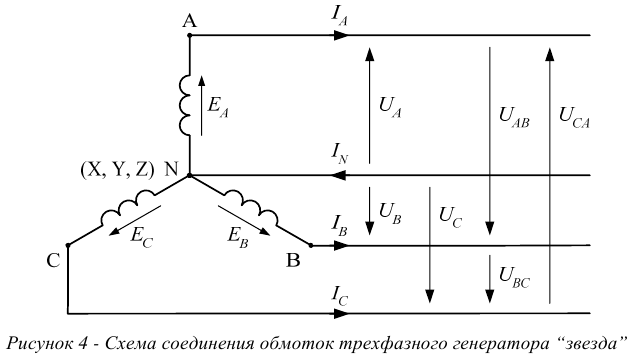
От начала обмоток  и нейтральной точки
и нейтральной точки  выводят провода, по которым энергия передается приемникам (потребителям). Провода, соединяющие начала обмоток источника и приемника называют линейными, а провод, соединяющий нейтральные точки источника питания и приемника — нейтральным проводом или нейтралью.
выводят провода, по которым энергия передается приемникам (потребителям). Провода, соединяющие начала обмоток источника и приемника называют линейными, а провод, соединяющий нейтральные точки источника питания и приемника — нейтральным проводом или нейтралью.
Напряжения 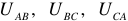 (рисунок 3) между линейными проводами, называют — линейными напряжениями, а токи
(рисунок 3) между линейными проводами, называют — линейными напряжениями, а токи 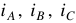 в линейных проводах — линейными токами.
в линейных проводах — линейными токами.
Напряжения 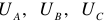 между нейтральным проводом и соответствующими линейными проводами называют фазными напряжениями.
между нейтральным проводом и соответствующими линейными проводами называют фазными напряжениями.
Положительное направление токов в линейных проводах принято в сторону потребителей, а в нейтральном проводе в сторону источника.
Соединение «звездой». Соотношения между токами и напряжениями. Симметричный и несимметричный режимы работы. Роль нулевого провода. Векторные диаграммы
Приемниками электрической энергии могут быть включены в трехфазную сеть двумя способами: «звездой» или «треугольником». На рисунке 5 представлена схема соединения генератора и нагрузки по схеме «звезда -звезда» с нейтральным проводом.
Напряжения 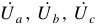 — фазовые напряжения приемника,
— фазовые напряжения приемника,  — фазные напряжения генератора. Из схемы видно, что
— фазные напряжения генератора. Из схемы видно, что

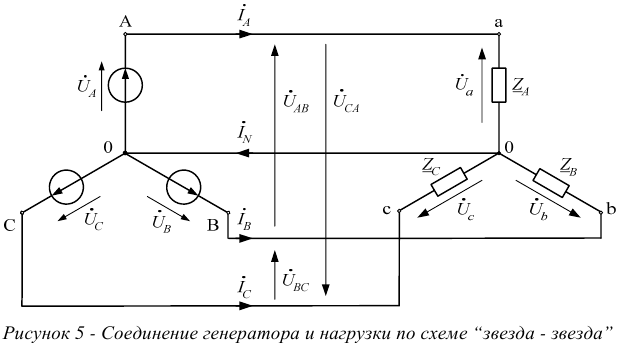
Соотношения между линейными и фазовыми напряжениями определяются в общем случае по второму закону Кирхгофа (в геометрической или комплексной форме):

При соединении потребителей «звездой», когда все линейные и фазовые напряжения равны 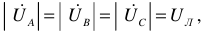 а
а 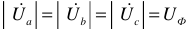 справедливо соотношение
справедливо соотношение

Ток в нейтральном проводе определяется по первому закону Кирхгофа

При симметричной нагрузке 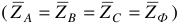 , ток в нейтральном проводе отсутствует, поэтому необходимость, в нем отпадает.
, ток в нейтральном проводе отсутствует, поэтому необходимость, в нем отпадает.
Векторная диаграмма цепи при симметричной нагрузке показана на рисунке 6, а.
При несимметричной нагрузке ток 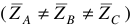 , токи в фазах различны, но за счет нейтрального провода напряжения на каждой фазе приемника с изменением нагрузки практически остается постоянным по величине и равным фазному напряжению генератора. Векторная диаграмма при несимметричной (неравномерной) нагрузке соответствует показанной на рисунке 6, а. При обрыве нейтрального провода, что является серьезной аварией, диаграмма принимает вид, показанный на рисунке 6, б. Возникает перекос фазных напряжений, зависящий от величин и характера нагрузки в фазах.
, токи в фазах различны, но за счет нейтрального провода напряжения на каждой фазе приемника с изменением нагрузки практически остается постоянным по величине и равным фазному напряжению генератора. Векторная диаграмма при несимметричной (неравномерной) нагрузке соответствует показанной на рисунке 6, а. При обрыве нейтрального провода, что является серьезной аварией, диаграмма принимает вид, показанный на рисунке 6, б. Возникает перекос фазных напряжений, зависящий от величин и характера нагрузки в фазах.
Таким образом, нейтральный провод обеспечивает симметрию фазных напряжений приемника при несимметричной нагрузке.
Соединение «треугольником». Соотношения между токами и напряжениями. Симметричный и несимметричный режимы работы. Векторные диаграммы
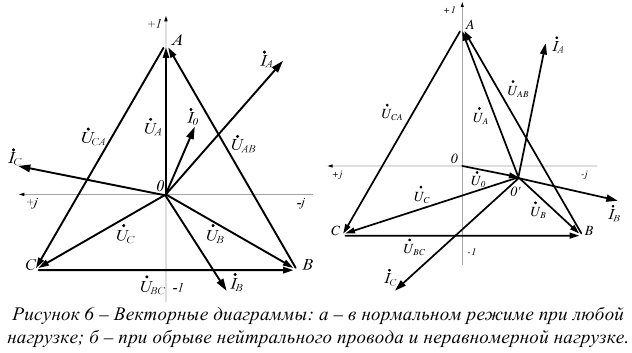
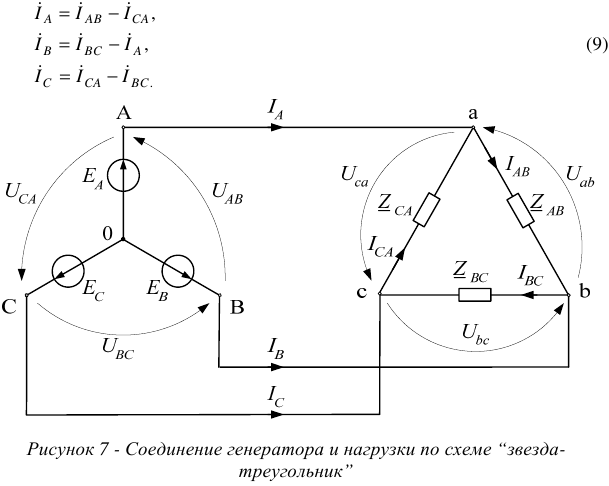
Генератор и потребитель могут быть соединена по схеме «звезда -треугольник» (см. рисунок 7).
При соединении потребителя «треугольником» фазные напряжения всегда равны соответствующим линейным:

Фазные и линейные токи не равны между собой, соотношения между ними можно получить по первому закону Кирхгофа (в геометрической или комплексной форме):
Векторная диаграмма при неравномерной нагрузке и соединении в треугольник приведена на рисунке 8.
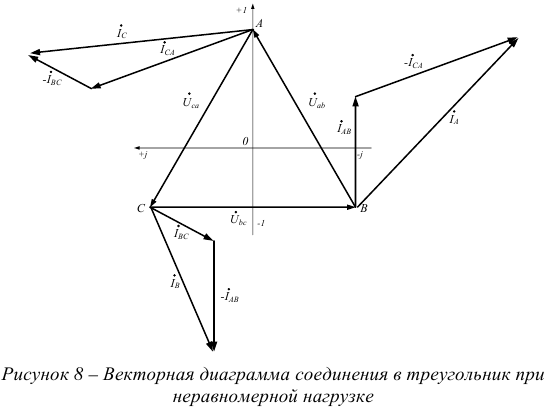
Независимо от характера нагрузки геометрическая сумма линейных токов равна нулю.

При симметричной нагрузке соотношение между модулями фазных  и линейных токов
и линейных токов  определяется выражением
определяется выражением

Мощность в трехфазной сети. Универсальная формула мощности
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз

здесь
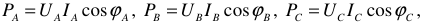
где 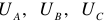 и
и 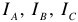 — фазные напряжения и токи;
— фазные напряжения и токи; 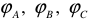 — углы сдвига фаз между напряжением и током.
— углы сдвига фаз между напряжением и током.
Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз

здесь
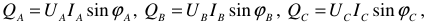
где 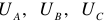 и
и 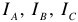 — фазные напряжения и токи;
— фазные напряжения и токи; 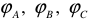 — углы сдвига фаз между напряжением и током.
— углы сдвига фаз между напряжением и током.
Полная мощность отдельных фаз

Полная мощность трехфазного приемника

При симметричной системе напряжений
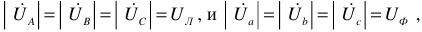
и симметричной нагрузке
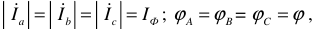
фазные мощности равны
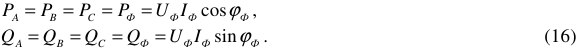
Активная мощность симметричного трехфазного приемника

Аналогично выражается и реактивная мощность

Выражения часто называют универсальными формулами мощности.
Из них следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат.
Измерение активной мощности в трехфазных цепях
Измерение активной мощности в трехфазных цепях производят с помощью трех, двух или одного ваттметров, используя различные схемы их включения. Схема включения ваттметров для измерения активной мощности определяется схемой сети (трех- или четырехпроводная), схемой соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная), доступностью нейтральной точки.
При несимметричной нагрузке в четырехпроводной цепи активную мощность измеряют тремя ваттметрами (рисунок 9), каждый из которых измеряет мощность одной фазы — фазную мощность.
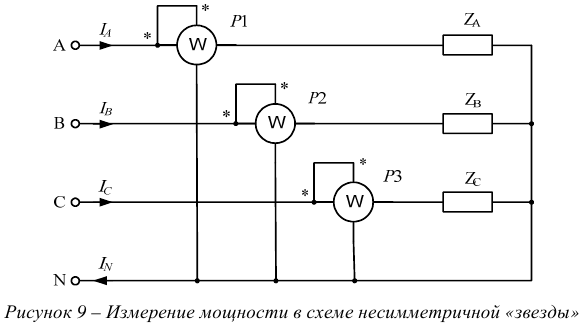
Активная мощность приемника определяют по сумме показаний трех ваттметров: 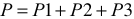 .
.
Измерение мощности тремя ваттметрами возможно при любых условиях.
При симметричном приемнике и доступной нейтральной точке активную мощность приемника определяют с помощью одного ваттметра, измеряя активную мощность одной фазы РФ по схеме рисунок 10. Активная мощность всего трехфазного приемника равна при этом утроенному показанию ваттметра: 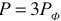 .
.
Измерение активной мощности симметричного приемника в трехфазной цепи одним ваттметром применяют только при полной гарантии симметричности трехфазной системы.
В трехпроводных трехфазных цепях при симметричной и несимметричной нагрузках и любом способе соединения приемников широко распространена схема измерения активной мощности приемника двумя ваттметрами (рисунок 11).
Показания двух ваттметров при определенной схеме их включения позволяют определить активную мощность трехфазного приемника, включенного в цепь с симметричным напряжением источника питания.
Активная мощность всей цепи здесь будет равна сумме показаний двух ваттметров: 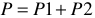 .
.
Для измерения активной мощности в трехфазных цепях промышленных установок широкое применение находят двухэлементные трехфазные электродинамические и ферродинамические ваттметры, которые содержат в одном корпусе два измерительных механизма и общую подвижную часть. Катушки обоих механизмов соединены между собой по схемам, соответствующим рассмотренному методу двух ваттметров. Показание двухэлементного ваттметра равно активной мощности трехфазного приемника.
Магнитные цепи
План контрольной работы:
- Основные величины, характеризующие магнитное поле и связь между ними.
- Закон полного тока. Магнитодвижущая сила. Магнитная цепь и ее разновидности.
- Основные характеристики ферромагнитных материалов. Роль ферромагнитных материалов в магнитной цепи.
- Вебер-амперные характеристики и их построение. Законы Кирхгофа и Ома для магнитных цепей.
- Расчет простых магнитных цепей.
Основные величины, характеризующие магнитное поле и связь между ними
Если электрический заряд неподвижен, то вокруг него существует одно поле — электрическое поле. Если электрический заряд движется, то вокруг него кроме электрического поля, образуется еще одно дополнительное силовое поле, которое называется магнитным полем.
Магнитное поле это поле движущегося заряда или тока. Так как ток -это упорядоченное движение электрических зарядов.
Возникая от движения зарядов, магнитное поле, в свою очередь действует только на движущийся заряд или ток. На неподвижный заряд магнитное поле не действует.
Для образования магнитных полей имеется два пути:
- а) за счет естественных магнитов;
- б) за счет искусственных магнитов — электромагнитов.
Чтобы изобразить поле используется графический метод — силовые линии.
Силовая линия, это линия, касательная, к каждой точке которой дает направление действующей силы в этой точке.
Силовые линии так же, как горизонтали у топографов позволяют изображать магнитные «бугры» и «ямы» в магнитном поле. По ним можно узнать области сильных и слабых полей.
Магнитное поле, как и поле тяготения Земли, силовое, векторное по-
Магнитное поле — направленное поле. Направление действия его указывается с помощью стрелок на силовых линиях.
Принято считать за положительное направление поля, а значит и силовых линий, направление от северного полюса  к южному
к южному 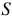 . То место, из которого силовые линии выходят, называются северным или положительным полюсом.
. То место, из которого силовые линии выходят, называются северным или положительным полюсом.
То место, в которое силовые линии поля входят, называется южным полюсом. Внутри магнита силовые линии направлены от южного полюса к северному.
Таким образом, силовые линии магнитного поля замкнутые на себя линии, они не имеют ни начала, ни конца. В этом коренное отличие силовых линий магнитного поля от силовых линий электрического поля, которые всегда имеют концы, на зарядах, создающих поле.
Вокруг уединенного прямолинейного проводника с током силовые линии представляют собой концентрические окружности. Общий центр, которых находится в центре проводника с током. И здесь силовые линии, замкнутые линии на себя и не имеют, ни начала, ни конца.
Направление действия магнитного поля определяется двумя способами:
- а) пробными магнитными стрелками;
- б) правоходовым винтом — штопором (буравчиком).
Правило штопора гласит:
Если штопор вворачивать так, чтобы жало двигалось в направлении тока, то вращающаяся ручка при этом укажет направление силовых линий магнитного поля.
Магнитное поле характеризуется тремя главными величинами или параметрами:
1) 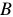 — магнитной индукцией или плотностью магнитного поля, измеряется в теслах;
— магнитной индукцией или плотностью магнитного поля, измеряется в теслах;
2) 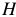 — напряженностью магнитного поля (магнитная сила поля — расчетная величина), измеряется а А/м;
— напряженностью магнитного поля (магнитная сила поля — расчетная величина), измеряется а А/м;
3) 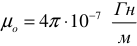 — абсолютной магнитной проницаемостью (характеризует влияние среды на образование магнитного поля в этой среде).
— абсолютной магнитной проницаемостью (характеризует влияние среды на образование магнитного поля в этой среде).
Эти величины связаны между собой выражением:

где 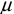 — относительная магнитная проницаемость.
— относительная магнитная проницаемость.
Для воздуха и для всех цветных металлов 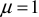 , поэтому
, поэтому 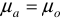 . Для ферромагнитных материалов
. Для ферромагнитных материалов 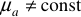 , кроме того значение относительной магнитной проницаемости для таких материалов намного больше единицы. Например: для трансформаторного железа
, кроме того значение относительной магнитной проницаемости для таких материалов намного больше единицы. Например: для трансформаторного железа 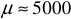 (трансформаторные сердечники), для пермаллоя
(трансформаторные сердечники), для пермаллоя 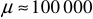 (сердечники реле, экраны), для серого чугуна
(сердечники реле, экраны), для серого чугуна 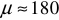 (корпуса электрооборудования).
(корпуса электрооборудования).
Магнитным потоком называется поток вектора индукции, взятый по всей площади, нормальной к этому потоку.
Если  и вектор индукции перпендикулярен площадке
и вектор индукции перпендикулярен площадке 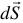 , то получим
, то получим

Магнитный поток измеряется в веберах.
Индукция или плотность магнитного потока измеряется в веберах на 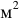 или в теслах.
или в теслах.
Закон полного тока. Магнитодвижущая сила. Магнитная цепь и ее разновидности
Закон полного тока — основной расчетный закон электротехники. Закон полного тока — экспериментальный закон. Он выведен на основании математической обработки опытных данных
Закон полного тока гласит:
Намагничивающая сила вдоль любого замкнутого контура равна полному току, пронизывающему этот контур.
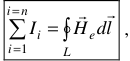
здесь
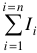
полный ток через контур.
Магнитодвижущая сила или намагничивающая сила вдоль контура. Она названа так по аналогии с электродвижущей силой.
Действительно,
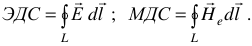
Намагничивающая сила действует аналогично ЭДС. Электродвижущая сила создает электрический напор, под действием которого по цепям идет ток. НС — создает магнитный напор, под действием которого создается магнитный поток.
Полным током через любой контур называется алгебраическая сумма токов, пронизывающих этот контур.
Полный ток любой катушки, которая имеет w витков, будет равен:
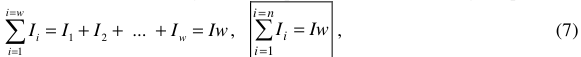
где  — ампервитки катушки.
— ампервитки катушки.
Знаки токов размечаются по правилу штопора (буравчика):
а) произвольно намечается направление положительного обхода по контуру;
б) применяя штопор, вращаем ручку в направлении выбранного обхода по заданному контуру. Жало штопора определяет направление протекания положительных токов.
В электрических машинах, трансформаторах, электромагнитных аппаратах и приборах весьма широко применяются цельные или наборные сердечники из электротехнической стали. Для чего это делается? Потому, что ферромагнитные материалы очень хорошо проводят через себя магнитные потоки. Железо в тысячи раз меньше препятствует магнитному потоку, чем воздух и все другие, например, цветные металлы.
В связи с указанным, при стальных сердечниках магнитный поток из воздуха и других сред устремляется в благоприятную для него среду -сталь.
По тем же соображениям почти невозможно вытянуть магнитный поток из стального сердечника в воздух.
В катушках без стального сердечника, магнитный поток хаотичен и не весь замыкается относительно всех витков.
При наличии сердечника, магнитный поток весьма уплотнен и замыкается вокруг всех витков. Силовые линии потока в сердечнике параллельны. Густота их более равномерна. Сердечник позволяет направлять поток по заранее намеченному пути. С помощью сердечника можно на разных участках пути потока сгущать линии или разрежать, а так же ответвлять те или иные потоки от главного.
Таким образом, сердечники из стали так же благоприятны для магнитных потоков, как медь или алюминий для электрических токов.
Магнитопроводы образуют магнитные цепи подобные электрическим цепям для тока. Магнитные цепи делятся на две группы: простые или неразветвленные; сложные или разветвленные.
Пример магнитных цепей показан на рисунке 1.
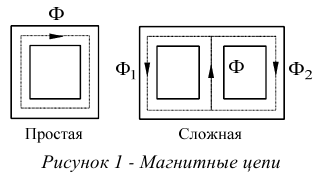
Кроме того, магнитные цепи бывают: а) замкнутые; б) разомкнутые.
Замкнутой магнитной цепью называют такую цепь, в которой магнитный поток на всем пути проходит по стальному сердечнику.
Разомкнутой магнитной цепью называют такую, в которой магнитный поток на всем своем пути не проходит по стали, а часть пути идет по воздуху.
Воздушные участки магнитной цепи называются воздушными зазорами.
Самое большое препятствие для магнитного потока — это воздушный зазор.
Магнитные цепи делятся на цепи: с постоянным сечением магнито-провода; с переменным сечением магнитопровода.
Основные характеристики ферромагнитных материалов. Роль ферромагнитных материалов в магнитной цепи.
Для магнитного поля в стальном сердечнике может записано соотношение:

Таким образом, стальные магнитопроводы являются нелинейными цепями.
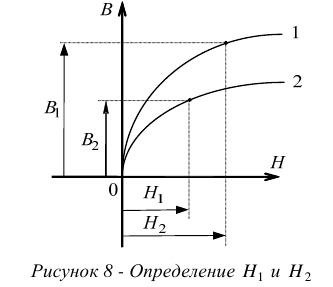
Зависимость индукции магнитного поля в стальном сердечнике от тока намагничивания, то есть от напряженности поля, показана на рисунке 2.
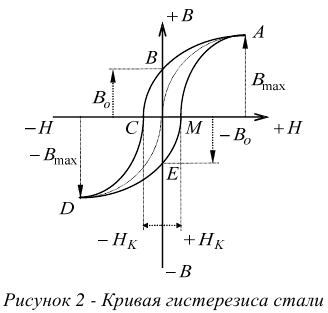
На рисунке 2:
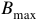 — точка насыщения стали;
— точка насыщения стали;
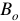 — остаточная индукция;
— остаточная индукция; 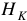 — коэрцитивная (задерживающая сила).
— коэрцитивная (задерживающая сила).
Процесс отставания магнитных свойств стали от намагничивающей силы называется гистерезисом.
Графически процесс гистерезиса выражается петлей гистерезиса.
Петля показывает, что намагничивание и размагничивание стали не совсем обратимые процессы. Часть энергии задерживается в стали. Эта энергия пропорциональна площади петли гистерезисного цикла. Задержанная энергия идет на бесполезное, и даже вредное нагревание сердечника и магнитопровода в целом. Создаются потери энергии, которые называются потерями на гистерезис и перемагничивание.
Чтобы уменьшить нагрев сердечников выпускают специальные электротехнические сорта стали. Для них гистерезис очень мал. Их часто называют магнитомягкими сталями. Если взять среднюю линию такой узкой петли. То мы получим усредненную линию, которая называется кривой намагничивания стали, рисунок 3.

Кривая намагничивания не имеет точного аналитического выражения. Поэтому для каждого материала ее получают опытным путем.
Между величинами, характеризующими магнитные и электрические цепи, существует формальная аналогия, позволяющая для магнитных цепей ввести ряд понятий, аналогичных понятиям, служащих для описания явлений в электрических цепях. Это распространяется и на методы расчета магнитных цепей.
В электрических цепях токи возникают под воздействием ЭДС.
В магнитных цепях магнитные потоки создаются ампервитками (намагничивающей силой или магнитодвижущей силой МДС).
Пользуюсь законом полного тока, можно получить: магнитные напряжения; магнитные сопротивления, проводимости.
Вебер-амперные характеристики и их построение. Законы Кирхгофа и Ома для магнитных цепей
Между величинами, характеризующими магнитные и электрические цепи, существует формальная аналогия, позволяющая распространить на магнитные цепи методы расчета цепей постоянного тока.
В электрических цепях токи возникают под воздействием ЭДС.
В магнитных цепях магнитные потоки создаются ампервитками (намагничивающей силой или магнитодвижущей силой МДС).
Пользуюсь законом полного тока, можно получить: магнитные напряжения; магнитные сопротивления, проводимости.
Рассмотрим неразветвленную магнитную цепь с переменным сечением участков I и 2, изображенную на рисунке 4.
Пусть нам известны геометрические размеры магнитопровода и магнитные характеристики материалов: 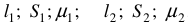 .
.
Найдем связь между магнитным потоком 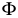 и МДС цепи
и МДС цепи 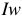 . Величины индукции на первом и втором участках цепи будут таковы
. Величины индукции на первом и втором участках цепи будут таковы
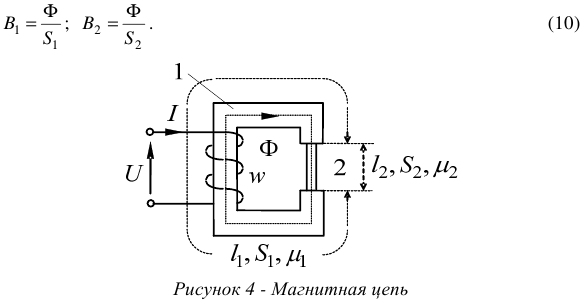
Напряженности поля на участках
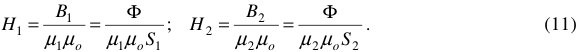
Применим закон полного тока к контуру, ограниченному средней
магнитной линией 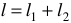 .
.
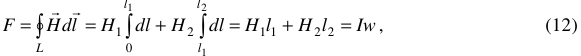
где 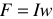 — намагничивающая сила (НС или МДС). Подставим (11) в (12) и получим
— намагничивающая сила (НС или МДС). Подставим (11) в (12) и получим

Обозначим:
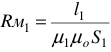 — магнитное сопротивление первого участка;
— магнитное сопротивление первого участка;
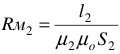 — магнитное сопротивление второго участка.
— магнитное сопротивление второго участка.
С учетом введенных обозначений запишем

где 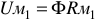 — магнитное напряжение на первом участке;
— магнитное напряжение на первом участке; 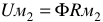 — магнитное напряжение на втором участке.
— магнитное напряжение на втором участке.
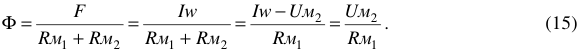
Уравнение (15) называется законом Ома для магнитной цепи. По выражению (15) можно составить эквивалентную расчетную схему неразветвленной магнитной цепи, рисунок 5.
Для магнитных цепей можно сформулировать законы Кирхгофа. Первый закон Кирхгофа для магнитной цепи.

Алгебраическая сума магнитных потоков в любом узле магнитной цепи равна нулю.
Потоки, притекающие к узлу, берутся со знаком плюс. Потоки, оттекающие от узла — берутся со знаком минус.
Второй закон Кирхгофа для магнитной цепи.

Алгебраическая сумма намагничивающих сил и магнитных напряжении в любом замкнутом контуре магнитной цепи равна нулю.
Расчет простых магнитных цепей
Магнитные цепи из ферромагнитных материалов являются нелинейными. Это значит, что магнитные сопротивления участков цепи не остаются постоянными и зависят от величины магнитных потоков, протекающих по нему. Поэтому, магнитные цепи, как цепи нелинейные, рассчитываются графоаналитическими методами.
Расчет имеет огромное практическое значение, так как большинство электротехнических устройств имеют магнитные цепи.
Обычно бывает задано для каждого участка магнитной цепи:
1) длина участка  ;
;
2) сечение участка  ;
;
3) материал участка;
4) кривая намагничивания 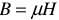 ;
;
5) число витков катушек 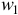 .
.
Магнитные цепи рассчитываются, в зависимости от поставленных условий, различно. На практике наиболее часто используется два варианта расчета.
1-й вариант (прямая задача). Заданы: магнитные потоки 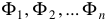 .
.
Требуется определить намагничивающие силы 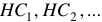 или токи в обмотках.
или токи в обмотках.
2-й вариант (обратная задача). Заданы: токи 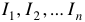 или намагничивающие силы
или намагничивающие силы 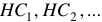 обмоток.
обмоток.
Требуется определить магнитные потоки во всех участках магнитной цепи 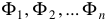 .
.
Рассмотрим решение задачи по первому варианту.
Цепь показана на рисунке 6.
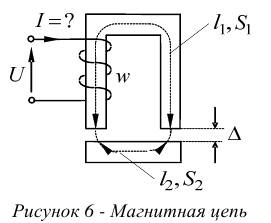
Дано:
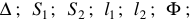 и кривые намагничивания всех участков цепи
и кривые намагничивания всех участков цепи 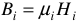
Найти:
Намагничивающий ток 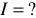 . Ход расчета.
. Ход расчета.
- Составляем расчетную схему, см. рисунок 7.
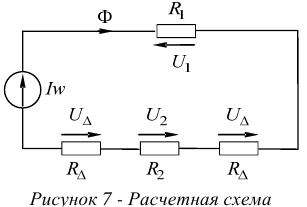
- Размечаем на схеме стрелки действия МДС.
Если дан ток в катушке и направление намотки витков, то направление действия МДС определяется по правилу штопора.
- Размечаем стрелку магнитного потока
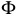 .
.
Стрелку 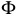 можно размечать произвольно, однако, в неразветвленной цепи ее можно определить правильно сразу. Положительное направление стрелки
можно размечать произвольно, однако, в неразветвленной цепи ее можно определить правильно сразу. Положительное направление стрелки 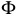 согласуется с действием МДС.
согласуется с действием МДС.
- Размечаем стрелки магнитных напряжений.
Стрелки размечаются параллельно элементам магнитных сопротивлений всегда против стрелки намеченного ранее магнитного потока 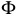 .
.
- Определяем магнитные индукции на каждом участке цепи
 .
.

- Определяем напряженности магнитного поля на участках стального магнитопровода.
Благодаря нелинейности цепи со сталью, определение  и
и  производим по кривым намагничивания этих участков, см. рисунок 8. Эти кривые должны быть заданы.
производим по кривым намагничивания этих участков, см. рисунок 8. Эти кривые должны быть заданы.
- Определяем напряженность поля в воздушных зазорах. Определить истинную картину распределение магнитного потока в воздушном зазоре — сложная задача. Для малых зазоров
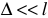 , магнитное поле в зазоре можно считать однородным. Распор магнитных силовых линий в зазоре будем считать отсутствующим. Тогда
, магнитное поле в зазоре можно считать однородным. Распор магнитных силовых линий в зазоре будем считать отсутствующим. Тогда

где 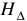 — напряженность магнитного поля в зазоре, в А/м;
— напряженность магнитного поля в зазоре, в А/м;
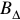 — плотность магнитного поля (индукция) в воздушном зазоре в
— плотность магнитного поля (индукция) в воздушном зазоре в 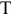 .
.
- Определяем магнитные напряжения.

- Определяем уравнения физического состояния цепи. Составление уравнений производится на основании двух законов
Кирхгофа любыми ранее рассмотренными методами расчета электрических цепей, кроме метода наложения.
В нашем случае по второму закону Кирхгофа имеем

Тогда получим

- Определяем ток в обмотке. В нашем случае,
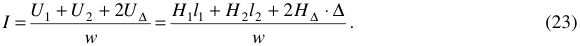
Решение обратной задачи.
Задача решается с помощью построения вспомогательной характеристики  .
.
Для построения характеристики составляется таблица вида:
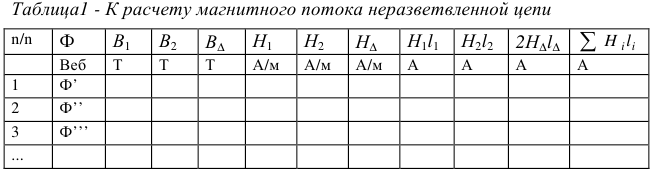
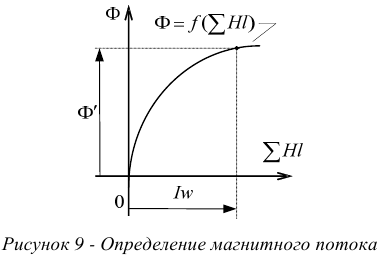
По данным таблицы 1 строят зависимость магнитного потока от падения магнитного напряжения в цепи (вебер-амперную характеристику) и графически определяют по ней искомое значение магнитного потока, как показано на рисунке 9.
Расчет разветвленной магнитной цепи так же основан на законах Кирхгофа. Вследствие нелинейности цепи расчет производится графоаналитическими методами.
В последнее время в связи, с широким применением ЭВМ, актуальность графоаналитических приемов расчета снизилась.
Переходные процессы в линейных цепях
План контрольной работы:
- Основные положения и определения.
- Включение катушки на постоянное напряжение. Короткое замыкание катушки с током. Энергия магнитного поля катушки.
- Заряд и разряд конденсатора. Энергия электрического поля конденсатора. Законы коммутации.
- Включение полной цепи
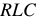 на постоянное напряжение.
на постоянное напряжение. - Операторный метод расчета переходных процессов. Теорема Хэви-сайда.
Основные положения и определения
Ранее, мы изучали установившиеся, стационарные режимы в электрической цепи. В таких режимах, электрическая энергия, связанная с цепью в виде магнитного и электрического полей остается неизменной.
Совершенно иное возникает при переходных, неустановившихся, нестационарных режимах. Например, при включении, отключении или переключении в электрических цепях. Здесь количество энергии связанное с цепью изменяется динамическим образом. В переходных процессах изменяются так же магнитные и электрические поля, связанные с цепью. В таких случаях нарушается постоянно действующая пропорция между напряжением, током, сопротивлением. В течение переходного режима сопротивление цепи так же не остается постоянным. Они меняются во времени.
Под установившимся режимом понимают такой, при котором общее количество энергии связанное с цепью в виде электрического и магнитного полей остается постоянным и от времени не зависит.
Переходным режимом (или процессом) называют такой, при котором общее количество энергии связанное с цепью в виде электрического и магнитного полей динамически изменяется во времени.
Таким образом, главной причиной, которая вызывает переходный процесс, является перераспределением энергии в цепи.
Переходный процесс не может происходить мгновенно, так как на перераспределение энергии требуется определенное (теоретически бесконечное) время.
Переходный процесс возникает при переходе от одного установившегося режима к другому, см. рисунок I.
Поэтому в начале и в конце он всегда связан с величинами напряжений и токов установившихся режимов.

где 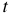 — время переходного режима;
— время переходного режима;
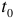 — начало переходного режима и, одновременно, конец первого установившегося режима (
— начало переходного режима и, одновременно, конец первого установившегося режима (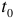 часто принимается равным нулю);
часто принимается равным нулю); 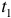 — конец переходного режима и, одновременно начало нового второго установившегося режима.
— конец переходного режима и, одновременно начало нового второго установившегося режима.
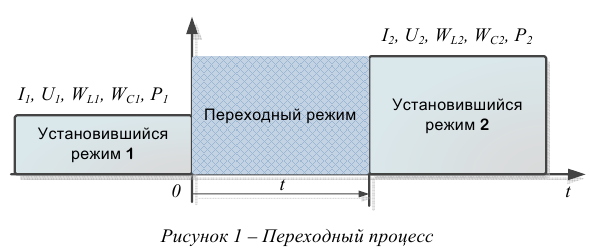
Теоретически  , практически это время искусственно ограничивают, когда влияние его на токи и напряжения становятся меньше одного процента.
, практически это время искусственно ограничивают, когда влияние его на токи и напряжения становятся меньше одного процента.
В обычных схемах переходные процессы протекают весьма быстро в течение долей секунды или секунд.
Из большого разнообразия переходных процессов инженерную практику интересуют главным образом коммутационные переходные режимы.
Коммутационными переходными режимами называются режимы, которые возникают при включении, выключении, коротких замыканиях, различного рода переключениях, внезапных изменениях параметров цепи.
Расчет переходных режимов весьма важен, так как только по этим данным можно правильно выбрать электрические машины, выключатели, устройства защиты, коммутационное оборудование и т.д.
Здесь мы будем рассматривать коммутационные переходные режимы только в линейных цепях с сосредоточенными параметрами.
Такие цепи и при переходных процессах подчиняются законам Ома и Кирхгофа, но для мгновенных значений и в дифференциальной форме.
Переходные процессы в нелинейных цепях точному аналитическому расчету не поддаются. В таких цепях законы Ома и Кирхгофа перестают существовать. Их анализируют численно на ЭВМ.
Условимся, что, исследуя цепи, мы будем всегда помнить о следующих нами принятых везде допущениях:
1) Источник энергии, питающий цепь, имеет мощность потенциально большую, чем мощность цепи  . В связи с этим при переходном режиме
. В связи с этим при переходном режиме 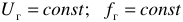 ;
;
2) Влиянием электрической дуги на контактах коммутационного устройства пренебрегаем;
3) Собственное время срабатывания коммутационной аппаратуры считаем равным нулю.
Включение катушки на постоянное напряжение. Короткое замыкание катушки с током. Энергия магнитного поля катушки
Включение катушки на постоянное напряжение
Рассмотрим, как изменяется ток  и напряжение
и напряжение  во время переходного режима при включении катушки (цепи
во время переходного режима при включении катушки (цепи  ) на постоянное напряжение, схема представлена на рисунке 2. Начальные условия процесса: при
) на постоянное напряжение, схема представлена на рисунке 2. Начальные условия процесса: при 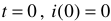 .
.
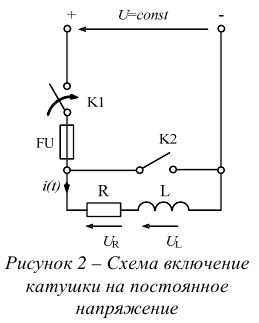
В момент времени  , ключ
, ключ  замыкается и начинается переходный процесс в катушке, представленной на схеме своими параметрами: индуктивностью
замыкается и начинается переходный процесс в катушке, представленной на схеме своими параметрами: индуктивностью 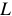 и активным сопротивлением
и активным сопротивлением  .
.
Электрическое равновесие цепи для любого момента времени будет:
но
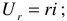

Тогда получаем

Мы имеем неоднородное линейное дифференциальное уравнение первого порядка.
Примечание
Его решение в общем виде запишется так:

где 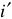 — частное решение уравнения (3) с правой частью;
— частное решение уравнения (3) с правой частью; 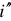 — общее решение этого же уравнения, но без правой части (она приравнивается к нулю).
— общее решение этого же уравнения, но без правой части (она приравнивается к нулю).
Каждое из решений должно удовлетворять своему уравнению, поэтому:

Пусть 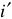 будет постоянной величиной
будет постоянной величиной 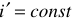 . Тогда частное решение примет вид
. Тогда частное решение примет вид

Из выражения (6) следует, что частное решение не зависит от времени и, следовательно, определяет установившийся ток.
Для общего решения имеем

Мы получили однородное линейное дифференциальное уравнение, общее решение уравнения (7) имеет вид:

где 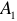 — постоянная интегрирования, которая связывает общее решение с конкретными условиями задачи;
— постоянная интегрирования, которая связывает общее решение с конкретными условиями задачи; 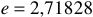 — основание натуральных логарифмов;
— основание натуральных логарифмов;
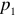 — корень характеристического уравнения;
— корень характеристического уравнения; 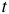 — время.
— время.
Характеристическое уравнение для данного дифференциального уравнения запишется так 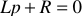 , отсюда
, отсюда

Корень характеристического уравнения  называют коэффициент затухания. Коэффициент затухания в физических задачах получается всегда отрицательным. Это значит, что во времени процесс изменения
называют коэффициент затухания. Коэффициент затухания в физических задачах получается всегда отрицательным. Это значит, что во времени процесс изменения  будет стремиться к нулю,
будет стремиться к нулю, 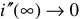 .
.
Размерность величины, обратной 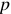 , соответствует размерности времени.
, соответствует размерности времени.
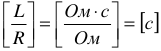 , поэтому вводят понятие постоянной времени
, поэтому вводят понятие постоянной времени  .
.

Учитывая соотношения (8) и (9) в выражении (7), получим

Из (11) видно, что;
1) Постоянной времени 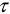 электрической цепи называется время, в течение которого переменная величина изменяется в основании натуральных логарифмов (2,71828 раз).
электрической цепи называется время, в течение которого переменная величина изменяется в основании натуральных логарифмов (2,71828 раз).
2) Через время 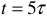 влияние времени на изменение переменной величины
влияние времени на изменение переменной величины  практически прекращается, так как
практически прекращается, так как  становится меньше одного процента, поэтому с точностью до 1% переходный процесс длится около
становится меньше одного процента, поэтому с точностью до 1% переходный процесс длится около 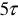 .
.

3) Длительность переходного режима в электрической цепи можно регулировать изменением параметров цепи 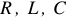 .
.
Постоянная интегрирования 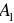 определится из заданных нам начальных условий.
определится из заданных нам начальных условий.
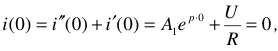
отсюда
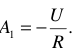
Решая дифференциальное уравнение (3) получим выражение для тока в при включении катушки на постоянное напряжение. Оно таково:

Напряжение на индуктивности определяется так:
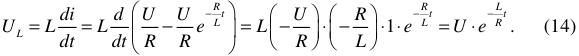
Построим графики 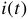 и
и 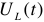 , то есть изобразим выражения (13) и (14) графически.
, то есть изобразим выражения (13) и (14) графически.
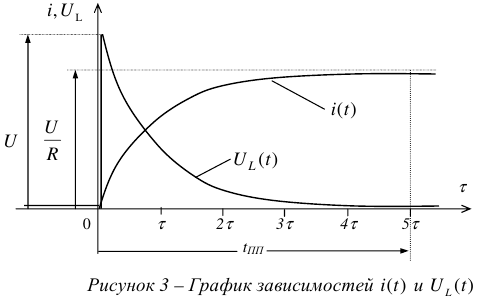
На основании выражений (13), (14) и графиков можно сделать следующие выводы:
1 Ток в момент включения катушки равен нулю, а затем плавно по экспоненциальному закону возрастает и через время 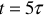 достигает установившегося значения и перестает зависеть от времени.
достигает установившегося значения и перестает зависеть от времени.
2 Напряжение на индуктивности катушки 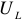 в момент включения скачком возрастает до величины напряжения источника, а затем плавно по экспоненциальному закону спадает и через время
в момент включения скачком возрастает до величины напряжения источника, а затем плавно по экспоненциальному закону спадает и через время 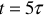 обращается практически в ноль.
обращается практически в ноль.
3 Напряжение на индуктивности 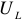 в первый момент включения полностью компенсирует напряжение источника
в первый момент включения полностью компенсирует напряжение источника 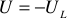 «запирает» источник, поэтому ток через катушку в первый момент после включения не проходит. Катушка как бы имеет бесконечно большое сопротивление (ветвь с катушкой как бы разорвана).
«запирает» источник, поэтому ток через катушку в первый момент после включения не проходит. Катушка как бы имеет бесконечно большое сопротивление (ветвь с катушкой как бы разорвана).
4 Часть энергии, поступающей в катушку, запасается в магнитном поле катушки.
Короткое замыкание катушки с током
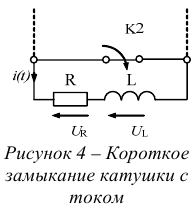
Ключом  замкнем накоротко катушку, по которой течет установившийся ток,
замкнем накоротко катушку, по которой течет установившийся ток, 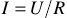 , см. рисунок 2. Предохранитель
, см. рисунок 2. Предохранитель  при этом сгорает и ветвь с катушкой оказывается отключенной от источника питания. Полученная схема приведена на рисунке 4.
при этом сгорает и ветвь с катушкой оказывается отключенной от источника питания. Полученная схема приведена на рисунке 4.
Очевидно, ток в катушке сразу не прекратится. Некоторое время он будет течь за счет запасов энергии в магнитном поле катушки. Направление тока не изменится благодаря реакционности закона электромагнитной индукции.
Электрическое равновесие цепи запишется так:
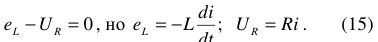
Тогда

Мы получили однородное линейное дифференциальное уравнение первого порядка.
Примечание
Решение уравнения (16) запишется в общем виде таким образом:

Характеристическое уравнение для данного дифференциального уравнения запишется так: 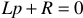 , отсюда
, отсюда

По тем же соображениям, что и ранее, длительность переходного режима при коротком замыкании  составит
составит
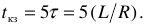
Постоянная интегрирования 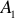 найдется из начальных условии.
найдется из начальных условии.
При
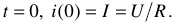
Тогда имеем:
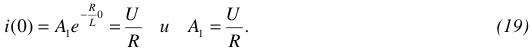
После решения уравнения (16), ток короткого замыкания в катушке запишется:

Закон изменения напряжение на катушке будет таким:
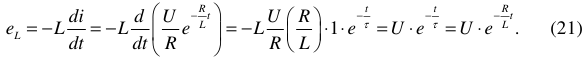
Построим графики по выражениям (20) и (21):
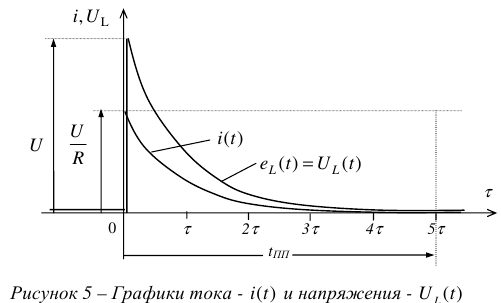
На основании выражений (20), (21) и графиков можно сделать следующие выводы:
1 Ток в момент короткого замыкания катушки не изменяется ни по величине, ни по направлению, а затем плавно по экспоненциальному закону снижается и через время  обращается практически в ноль.
обращается практически в ноль.
2 Напряжение на индуктивности в момент короткого замыкания изменяется скачком от нуля до напряжения источника, который питал катушку до короткого замыкания. Это напряжение (ЭДС катушки) создает и поддерживает ток в режиме короткого замыкания. Оно спадает по экспоненциальному закону и через время  обращается в ноль.
обращается в ноль.
3 Переходные процессы включения и короткого замыкания катушки протекают с одной и той же постоянной времени и имеют одну и ту же продолжительность.
4 Переходный процесс прекращается, когда запас энергии в магнитном поле катушки исчерпывается. При коротком замыкании энергия магнитного поля превращается в тепловую энергию на сопротивлении  и рассеивается в окружающее пространство.
и рассеивается в окружающее пространство.
Энергии магнитного ноля катушки
Чтобы определить энергию магнитного поля катушки, достаточно рассчитать энергию, которая переходит в тепло на сопротивление 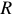 при коротком замыкании.
при коротком замыкании.

Проинтегрируем выражение (22), тогда получим:
Согласно (23) энергия магнитного поля катушки связана только с током и от напряжения не зависит.
Заряд и разряд конденсатора. Энергия электрического поля конденсатора. Законы коммутации
Заряд конденсатора
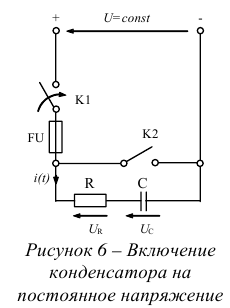
Рассмотрим, как изменяется ток 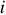 и напряжение
и напряжение 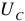 во время переходного режима при включении емкости на постоянное напряжение. Схема цепи представлена на рисунке 6.
во время переходного режима при включении емкости на постоянное напряжение. Схема цепи представлена на рисунке 6.
В момент времени  ключ
ключ  замыкается, и начинается переходный процесс заряда конденсатора, представленного на схеме своими параметрами: емкостью
замыкается, и начинается переходный процесс заряда конденсатора, представленного на схеме своими параметрами: емкостью 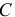 и активным сопротивлением соединительных проводов
и активным сопротивлением соединительных проводов 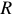 . Начальные условия процесса: при
. Начальные условия процесса: при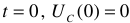 .
.
Электрическое состояние цепи для любого момента времени будет:
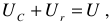
но
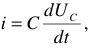
поэтому
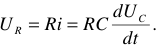
Подставим выражения (26) в (25), тогда получим:

Примечание
Решение уравнения (27) будет таким:
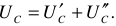
Далее расчет проводим, как и для катушки.
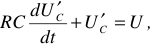
отсюда при
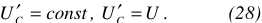
Для переходной составляющей процесса 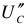 имеем
имеем

Характеристическое уравнение цепи будет таким: 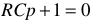 . Откуда определим корень данного уравнения или коэффициент затухания:
. Откуда определим корень данного уравнения или коэффициент затухания:

Решение уравнения (28) ищем в виде

Размерность величины, обратной  , соответствует размерности времени
, соответствует размерности времени
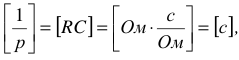
поэтому вводят понятие постоянной времени 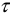 , равной
, равной

Здесь постоянная времени имеет тот же физический смысл, как и 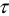 в цепи
в цепи 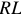 . Переходный процесс и здесь будет длиться:
. Переходный процесс и здесь будет длиться:

Решение уравнения (27) получим, подставив в него (28) и (31).

Постоянная интегрирования 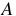 найдется из начальных условий.
найдется из начальных условий.
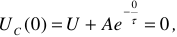
откуда

Подставим (35) в (27) и получим закон изменения напряжения на конденсаторе в переходном процессе,

Ток через конденсатор определяется по закону Ома для диэлектрика:
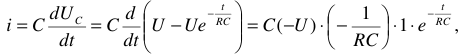
или окончательно имеем

Построим выражения (36) и (37) графически, см. рисунок 7.
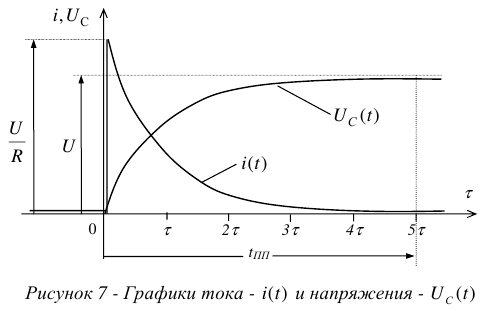
На основании выражений (36), (37) и графиков можно сделать следующие выводы:
1 Напряжение в момент включения конденсатора равно нулю (конденсатор как бы короткозамкнут), а затем плавно по экспоненциальному закону возрастает и через время 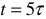 достигает установившегося значения и перестает зависеть от времени.
достигает установившегося значения и перестает зависеть от времени.
2 Ток на емкости 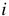 в момент включения скачком возрастает от нуля до величины
в момент включения скачком возрастает от нуля до величины 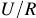 , а затем плавно по экспоненциальному закону спадает и через время
, а затем плавно по экспоненциальному закону спадает и через время 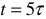 обращается в нуль. Величина тока в первый момент ограничивается только сопротивлением
обращается в нуль. Величина тока в первый момент ограничивается только сопротивлением 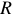 .
.
3 Часть энергии, поступающей в емкость, запасается в виде электрического поля в диэлектрике емкости (в виде электрической деформации диэлектрика).
4 Переходный процесс прекращается, когда запас энергии в электрическом поле конденсатора исчерпывается. При коротком замыкании энергия электрического поля превращается в тепловую энергию на сопротивлении 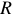 и рассеивается в окружающее пространство.
и рассеивается в окружающее пространство.
Разряд конденсатора
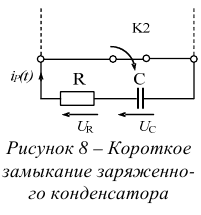
Закоротим накоротко емкость, на которой действовало установившееся напряжение  для чего замкнем ключ
для чего замкнем ключ  . Предохранитель
. Предохранитель 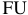 при этом сгорает, и ветвь с конденсатором оказывается отключенной от источника питания. Полученная схема приведена на рисунке 8.
при этом сгорает, и ветвь с конденсатором оказывается отключенной от источника питания. Полученная схема приведена на рисунке 8.
Очевидно, что напряжение на емкости сразу не исчезнет. Оно некоторое время будет действовать за счет запасов энергии в электрическом поле емкости.
Электрическое состояние цепи может быть выражено таким образом:

Под действием напряжения 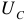 ток короткого замыкания
ток короткого замыкания 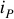 будет течь в сторону, противоположную зарядному току.
будет течь в сторону, противоположную зарядному току.
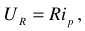
но
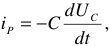
тогда
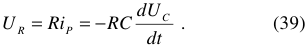
Подставим (39) в (38):

Мы получили однородное дифференциальное уравнение первого порядка.
Примечание.
Уравнение (40) решается так:

Характеристическое уравнение будет  . Решением его является соотношение:
. Решением его является соотношение:

Длительность процесса разряда конденсатора и здесь равна пяти постоянным времени —  .
.
Постоянная интегрирования 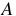 найдется из начальных условий.
найдется из начальных условий.
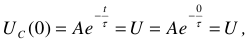
окончательно имеем
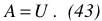
Решением уравнения (40) будет:

Ток через емкость будет изменяться по следующему закону:

На основании выражений (44) и (45) построим графики, изображенные на рисунке 3.8.
Какие же можно сделать выводы?
1 Напряжение в момент короткого замыкания емкости не изменяется ни по величине, ни по направлению, а затем плавно по экспоненциальному закону снижается и через время 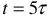 обращается в ноль.
обращается в ноль.
2 Ток в момент короткого замыкания емкости изменяется скачком от нуля до 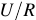 , а затем спадает до нуля.
, а затем спадает до нуля.
3 Переходные процессы включения и короткого замыкания емкости протекают с одной постоянной времени и продолжаются одинаковое время.
4 Переходный процесс заканчивается, когда запас энергии в электрическом поле емкости исчерпывается.
Энергия электрического поля емкости
Чтобы определить энергию электрического поля емкости поступим так же, как и для индуктивности.
Подсчитаем количество тепла, которое выделится на активном сопротивлении цепи, в процессе разряда конденсатора.
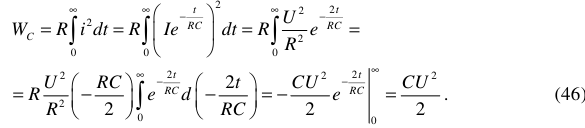
Законы коммутации
На основании рассмотренных переходных процессов можно сформулировать два закона коммутации.
Первый закон коммутации
В любой ветви с индуктивностью ток и магнитный поток в момент коммутации сохраняют те же значения, которые они имели до коммутации, и дальше начинают изменяться именно с этих значений.
Второй закон коммутации
В любой ветви с емкостью напряжение и заряд в момент коммутации будут иметь те же значения, которые они имели до коммутации, и в дальнейшем будут изменяться, начиная именно с этих значений.
Включение полной цепи  на постоянное напряжение
на постоянное напряжение
Цепь с последовательным соединением элементов  и
и  показана на рисунке 10.
показана на рисунке 10.
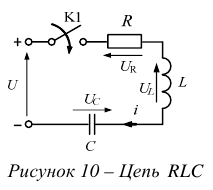
Электрическое равновесие цепи, согласно второму закону Крихгофа, запишется так:
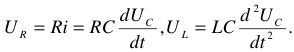
Поэтому можно записать:
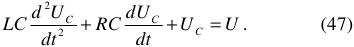
Решение неоднородного дифференциального уравнения второго порядка (47) обычно отыскивается в виде

Согласно выражению (48) процесс в данной цепи можно рассматривать состоящим из двух накладывающихся друг на друга процессов — принужденного, который как бы наступил сразу, и свободного, имеющего место только во время переходного режима.
Под принужденным режимом понимают электрическое состояние цепи, которое установится после окончания переходного процесса.
Видим, что принужденный режим в данном случае таков:
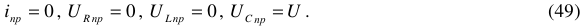
Видим, что характер переходного процесса определяется только свободным режимом.
Под свободным режимом понимают процесс, который происходит за счет энергии запасенной внутри цепи. Когда эта энергия преобразуется в тепло на активном сопротивлении цепи, переходный процесс закончится.
В этом режиме дифференциальное уравнение (47) будет иметь вид:
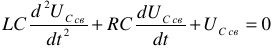
или разделив все на 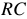 ,
,

Характеристическое уравнение в данном случае будет иметь вид:

Характер свободного процесса будет определяться видом корней характеристического уравнения (51).

Из выражения (52) видно, что корни характеристического уравнения 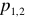 могут иметь три основных вида.
могут иметь три основных вида.
Апериодический переходами процесс (корпи характеристического уравнения вещественные, отрицательные и разные)
При таких корнях переходный процесс в электрической цепи называется апериодическим. Для апериодического режима в нашем случае имеем:
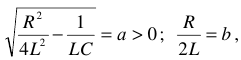
тогда
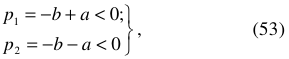
где 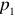 и
и 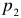 — коэффициенты затухания, при этом
— коэффициенты затухания, при этом 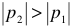 . Так как
. Так как 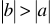 и
и 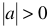 то корни вещественные.
то корни вещественные.
Это значит, что вторая составляющая свободного процесса будет затухать быстрее, чем первая.
Постоянные времени составляющих переходного процесса будут таковы:

Это значит, что переходный процесс второй составляющей короче первой. Общее время переходного процесса определяется по наибольшей постоянной времени 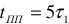 .
.
С другой стороны:
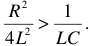
Поэтому
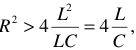
отсюда имеем

где  — активное сопротивление цепи;
— активное сопротивление цепи; 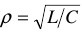 — волновое сопротивление цепи или резонансное сопротивление.
— волновое сопротивление цепи или резонансное сопротивление.
Апериодический режим может существовать только тогда, когда активное сопротивление цепи больше двух волновых или резонансных сопротивлений этой же цепи.
Решение уравнения (47) дает следующие результаты:
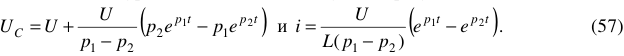
Изобразим полученные величины на графике (рисунок 11) при постоянных времени  .
.
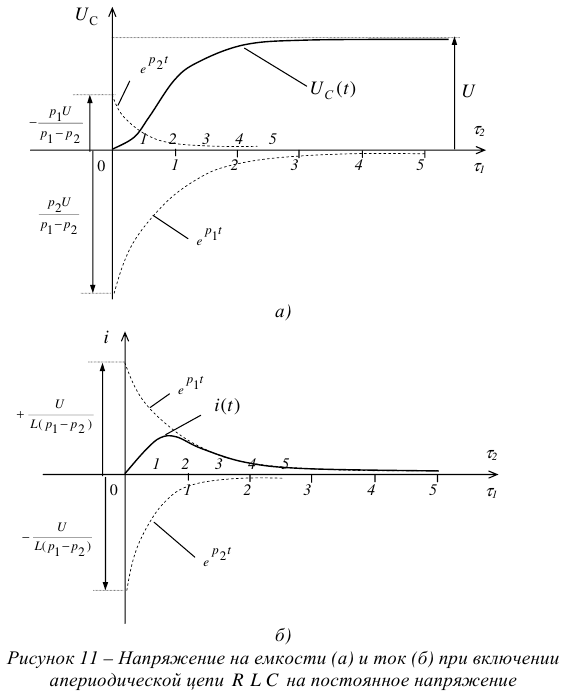
Колебательный переходный процесс (корпи характеристического уравнения сопряженные комплексные, с отрицательной вещественной частью)
При таких корнях переходный процесс в электрической цепи называется колебательным.
Для колебательного режима в нашем случае имеем:
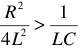
или
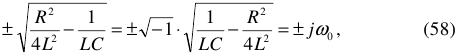
где  — собственная частота колебаний цепи.
— собственная частота колебаний цепи.
Период колебаний в контуре будет  .
.
Корни характеристического уравнения:

С другой стороны 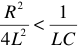 , поэтому
, поэтому 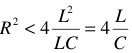 , отсюда имеем
, отсюда имеем

Колебательный переходный процесс затухает с коэффициентом затухания 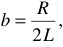 поэтому общее время данного переходного процесса можно оценить, как
поэтому общее время данного переходного процесса можно оценить, как 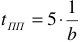 .
.
Колебательный режим может существовать только тогда, когда активное сопротивление цепи меньше двух волновых или резонансных сопротивлений этой же цепи. Решения уравнения (47) для данного случая таково:
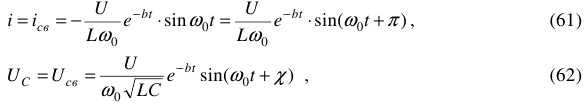
При определении постоянных интегрирования в данном случае, необходимо принять напряжение установившегося режима на емкости равным нулю. На рисунке 12 зависимости (61) и (62) показаны графически.
Затухание колебаний в контуре происходит за счет поглощения энергии в активном сопротивлении цепи.
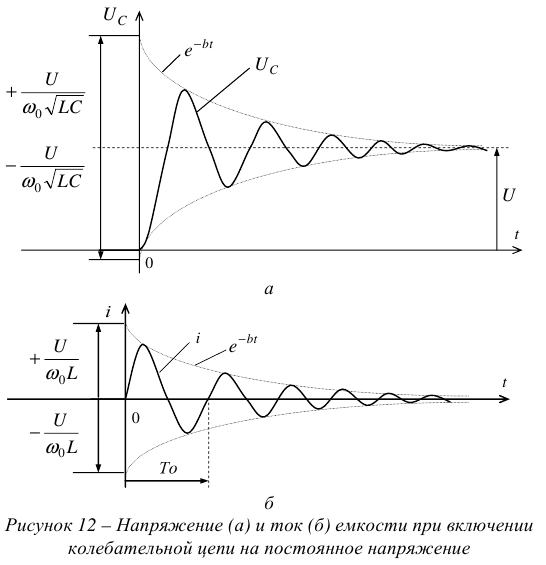
Критический или граничный переходный процесс (корни характеристического уравнения вещественные, отрицательные и равные)
При таких корнях переходный процесс в цепи называется критическим, граничным или предельным.
Для граничного режима имеем 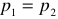 .
.
Постоянные времени будут одинаковыми 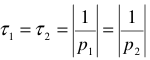 .
.
Такой режим наступает в цепи, когда активное сопротивление цепи равно двум волновым сопротивлениям этой же цепи

По своему характеру указанный режим является предельным случаем апериодического режима. Такой режим является промежуточным между апериодическим и колебательным режимами. Он весьма неустойчив. Малейшее нарушение соотношения между параметрами и процесс переходит либо в зону колебательного, либо в зону апериодического режимов, поэтому граничный режим на практике не используется и в данной работе не исследуется.
Часто преподаватели задают контрольные работы на операторный метод расчёта переходных процессов:
Возможно эти дополнительные страницы вам будут полезны:

