Одновременное действие изгиба и кручения. Изгиб и кручение валов круглого поперечного сечения

Одновременное действие изгиба и кручения. Изгиб и кручение валов круглого поперечного сечения

Одновременное действие изгиба и скручивания. Изгиб и скручивание вала круглого сечения Выше, при рассмотрении кручения (см. стр. 238), я предположил, что круглый вал будет подвергнут простому twist. In в реальном мире приложения, крутящий момент и изгибающие моменты часто действуют одновременно.

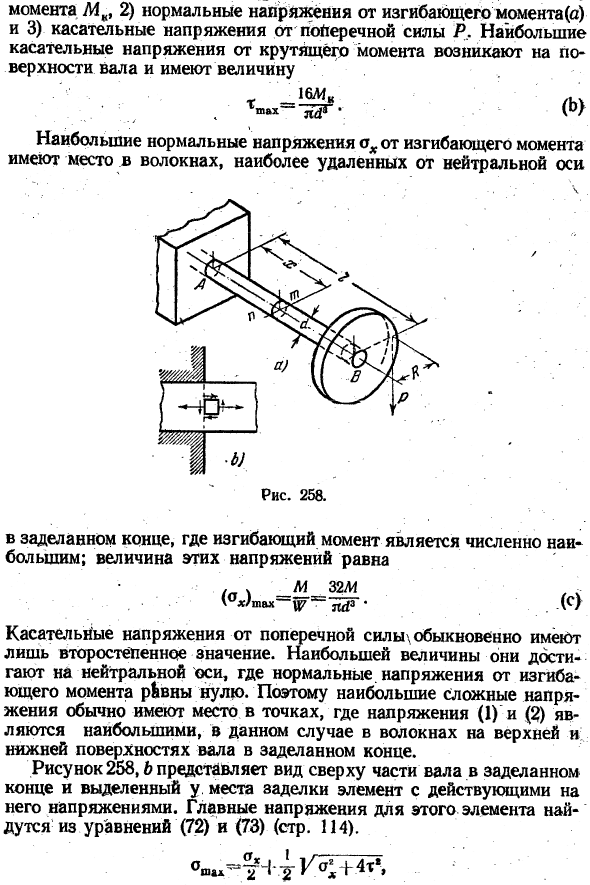
• Усилия, передаваемые на вал шкивом, шестерней или маховиком, могут приводить к скручивающим или изгибающим силам. Простой случай такого рода показан на рисунке. 258. Круглый вал загерметизирован на одном конце и/?Вертикальная сила P приложенная на расстоянии ofOff axis. In в этом случае крутящий момент MK-RI и боковая сила P на свободном конце уменьшаются до осевой нагрузки1).

Вращающий момент постоянн вдоль оси и изгибающий момент причиненный усилием P любого раздела равен М ^ — Р (/ -*). (ля） При поиске максимального напряжения, создаваемого в валу, необходимо учитывать: 1) напряжение сдвига от момента Mk, 2) нормальное напряжение от изгибающего момента (a), 3) напряжение сдвига от боковой силы R.

Максимальное напряжение сдвига от момента имеет значение с валом, которое будет возникать на поверхности. Людмила Фирмаль

Максимальное нормальное напряжение из-за изгибающего момента возникает в волокнах, наиболее удаленных от нейтральной оси Рисунок 258. / На закрытом конце изгибающий момент численно максимум. Величина этих напряжений равна. (V m 32 / I \уже / максимум Ts7 *• (С） Тангенциальное напряжение из-за силы сдвига\обычно имеет лишь второстепенное значение. Они достигают максимальной величины на нейтральной оси, где нормальное напряжение от изгибающего момента pb равно zero.

Обычно максимальное комплексное напряжение возникает в точке, где напряжения(1)и (2) равны maximized. In в этом случае она возникает на волокнах верхней и нижней поверхностей вала закрытого конца. На фиг. 258, б показан вид сверху части вала на герметичном конце и напряженного элемента в герметичном месте.

• Основные напряжения этого элемента определяются уравнениями (72)и (73) (стр. 114), которые можно найти из: Или, используйте формулы(B)и© в、 * я. х = 2р(М + ^ М1 + ЛГ’) = ^(м + KMCH1:). (163） Аналогично, используя формулу (73), получаем следующее: oy1n = 2 ^(м-/ МХ ^)= ^ я(м-Ул + у). (163 ’）

Из Формулы (163) можно отметить, что otax имеет то же значение, что и простой изгиб вала, если удельный эквивалентный изгибающий момент равен следующим значениям: Л * га = Г(М + Э * + АФ. Формула (34) (стр. 52) максимальное касательное напряжение рассматриваемого элемента (рис. 258, Б)составляет、 2 a «» a = — G. USHSCH,(164）

На практике обычно применяется теория максимального напряжения сдвига, которая определяет безопасные размеры диаметра точек мягкого металла. когда [t]указывает допустимое напряжение сдвига и заменяет его вместо tm в Формуле.

Для определения диаметра вала получается следующее уравнение Людмила Фирмаль

Приведенные выше рассуждения можно также применить к расчету полого вала наружного диаметра d и внутреннего диаметра Lx. и далее… ^ B и СГ 11] * А затем получаем из настроек (1×1y = n, уравнения для полого вала(163) и (163′). (М + Уш + Х),. (166)） Э ^ + у-(ж?） Максимальное напряжение сдвига равно г-ВММ + м (168） тахометр 1-л4)\ та = г » м-н) ум+ к- (169)）

Откуда? Если на вал действуют несколько параллельных поперечных сил, то для определения требуемого диаметра по формуле (165) или (169) необходимо получить суммарный изгибающий момент M и максимальный крутящий момент Mk в каждом сечении. Если боковые силы, действующие на валы, не параллельны, то возникающий из них изгибающий момент следует определять методом сложения вектора.

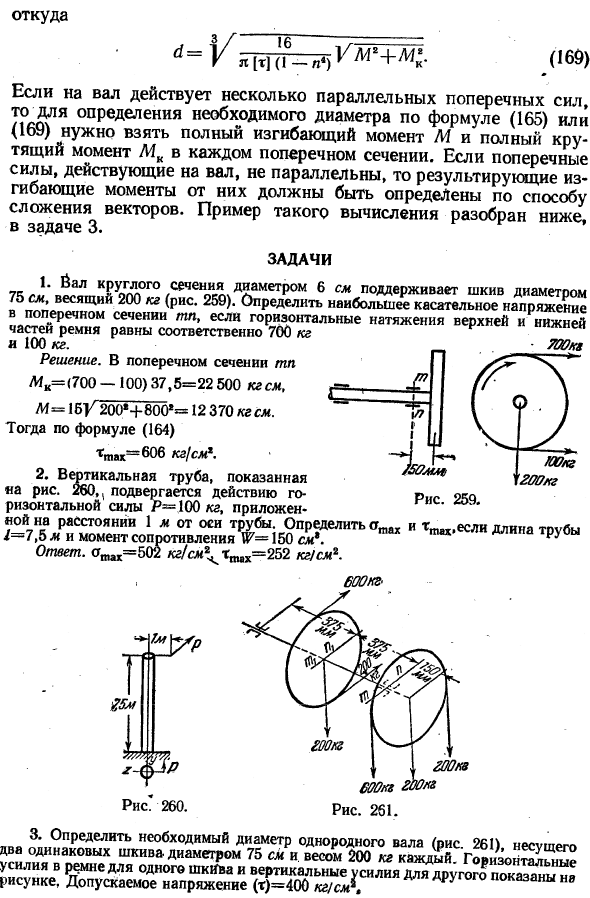
Примеры таких расчетов рассматриваются в задаче 3 ниже. Задачи 1.Круговые Яры диаметром 6 см, опорные шкивы диаметром 75 см, Масса 200 кг(рис. 259).Определить максимальное касательное напряжение поперечного сечения ТП, если горизонтальное натяжение верхней и нижней частей ремня равно 700 и 100 кг соответственно. The solution. In поперечное сечение, Мп МК = <700-100) 37,5 = 22 500 кг см、 M = 15U. 200 * + 800 * = 12 370 кг. 次に 、 式（164） ’gtak = 606 кг / см *. 2.

Вертикальные трубы показаны на рисунке. 260м подвергается воздействию более чем 259 городов. Горизонтальная сила р-на расстоянии 1 м от оси трубы прикладывается сила 100 кг. Длина трубы/ = 7,5 м и момент сопротивления нет. Для = 150 см9 определите<tmax и mtvh. Ответ. сгтах = 502 кг! cm2 ^ xplx = 2b2 кг / СМГ.

Рисунок: G 260 Рисунок 261. 3.Диаметр 75 см, Вес 200 кг, определяет необходимый диаметр однородного вала, поддерживающего 2 одинаковых шкива (рис.261).На рисунке показана горизонтальная сила ремня одного шкива и вертикальная сила другого шкива. Допустимое напряжение (t)= 400 кг / см *、

Смотрите также:

Предмет сопротивление материалов: сопромат 

Энергия упругой деформации при растяжении	Вал прямоугольного поперечного сечения
Растяжение, вызываемое ударом	Винтовая пружина с малым шагом витков