Оглавление:





Винтовая пружина с малым шагом витков
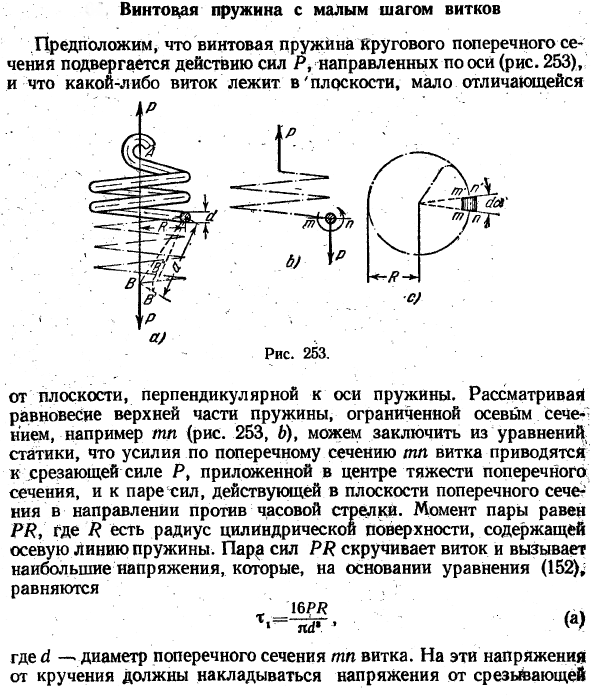
Спиральная пружина малого шага Предположим, что спиральная пружина круглого сечения подвергается действию направленной силы Р вдоль оси (рис. 253), а некоторые витки находятся в несколько иной плоскости. Икс-* Рисунок 253. От плоскости, перпендикулярной оси пружины.
- Рассматривая верхнее равновесие пружины, окруженной осевым сечением, например, mn (рис.253, 5), из уравнения статики можно сделать вывод, что сила вдоль поперечного сечения катушки mn сводится к сдвигающей силе P, приложенной к центру тяжести сечения и к паре сил, действующих против часовой стрелки в плоскости момента пары, равного PP, где P-радиус цилиндрической поверхности, включая ось пружины.
Пара сил PP закрутит катушку и причинит максимум stress. It основан на Формуле (152).Равный т■(а) Где d-диаметр сечения катушки mn. Эти напряжения кручения должны накладываться на напряжение от силы сдвига P. In в грубом приближении эта сила считается равномерно распределенной по поперечному сечению.
Тогда соответствующее касательное напряжение равно ’<си> В точке m (рис. 253,б) направления m1 и x2 совпадают, так что здесь возникает наибольшее касательное напряжение, величина которого равна ’^- ри, — ^(1 + Д). (160) 2-й раздел в скобках, представляющий силу сдвига,///?
Можно видеть, что с увеличением срока службы большое практическое значение приобретают тяжелые резьбовые пружины, применяемые в железнодорожных транспортных средствах. Людмила Фирмаль
Точки, такие как t внутри поворота, находятся в более неблагоприятных условиях, чем точки, такие как p. из опыта тяжелых пружин трещина обычно начинается с внутренней стороны поворота. 。 Рисунок 254.
Есть еще одна причина, по которой вы должны ожидать высокое напряжение внутри катушки. ^При расчете напряжения кручения мы использовали полученную формулу (a) для цилиндрического rod. In фактически, каждый пружинный элемент находится в состоянии, показанном на схеме. 254.
Если во время кручения участок b / поворачивается относительно ac, то можно видеть, что движение точки b относительно точки a совпадает с движением участка b / относительно точки cDue к тому, что расстояние ab меньше расстояния c/, относительный сдвиг внутреннего ab больше относительного сдвига внешнего c/, поэтому пара сил P /?
- Напряжение сдвига, вызванное . Учитывая это, необходимо рассчитать максимальное тангенциальное напряжение с учетом влияния сдвиговых сил, заменив 1) Формулу (160) формулой: _ , 16PR(4 / s-1,0. 615 \ * 2 /? В-г 1) такое исследование может быть проведено в V. R o e v e gh> m, Z. Ver, deut.
Например, т. к.57, стр. 1906.1913;кроме того, я waulam, трансформатор с ASME, 1928.Последние определяли напряжение опытным путем, используя измеренные значения поверхности катушки. Полное исследование различных видов пружин, Wahl, om, cit. А п. а.188.、 Мы видим, что поправочный коэффициент в скобках увеличивается с уменьшением m. например, если m = 4, то этот коэффициент составляет около 1,40, а если m = 10, то 1,14.
При расчете удлинения пружины или опускании ее нижнего конца обычно допустим только эффект скручивания обмотки. Для определения угла наклона спирали элемента между смежными 2-мя поперечными сечениями tn и t’l’(рис. 263,в) используйте формулу (161), а не/、 П. С. При скручивании нижняя часть пружины вращается относительно центральной mn (рис.263, а), а точка действия силы B представляет собой небольшую дугу BB, равную asif.
Вертикальная составляющая этого движения. Людмила Фирмаль
Полный спуск пружины получается суммированием спуска t’p», вызванного каждым элементом по длине пружины. И затем… (162)) Где n — количество оборотов. 。 。 Для пружин некруглого поперечного сечения вышеуказанный метод может быть применен для расчета напряжений и деформаций, когда формулы (151) и (152) заменяются формулами, соответствующими заданной форме поперечного сечения.
Например, для прямоугольного поперечного сечения должны быть применены уравнения (158) и (159). Задачи 1.Определите максимальное напряжение и удлинение спиральной пружины (рис. 253). P = 100 кг, p = 10 см, (1 = 2 см, число витков-20, a = 8 * 10e кг! см.* Ответ. tgaah = 726 кг / см2, 6 = 10 см. 2.
Решим предыдущую задачу, предположив, что поперечное сечение катушки составляет 2 см. Сторона. Решение. Если предположить, что поправочный коэффициент сдвигающей силы, зависящий в данном случае от кривизны витков (см. формулу (161)), такой же, как и в случае кругового сечения, то он получается из Формулы (158). Яд.、»100-10-1.14 1″»1-6.2086 * ’0.208-2 * = 696 кг [см2 При расчете удлинения, 0.141 (P (см. уравнение (159))) вместо nd * l32.И затем… А * 6. * g * 7 см. 32-6, Ифт 3.
Сравните вес 2 спиральных пружин (1 круглая, другая 1 1/4 квадратного сечения), принятых в задаче 1 и разработанных в условиях, которые не имеют одинакового максимального напряжения. Поправочный коэффициент в обоих случаях равен Припяти * 1,14.Сравните удлинение этих стержней. Рисунок 255. Решение. Длина стороны квадрата поперечного сечения найдена и z-уравнение Рисунок 256. nL3 / 16 = 0.2086*, оттуда b = * \ / 0.9440.98 L.
Масса пружины находится в том же соотношении т, что и поперечное сечение area. In другие слова、 ^. ( 0.98 Ш) ’ = 0.816. 2 удлинение пружины связано 0.141 * 0.141.0.926:^ = 1.33. 4.На рисунке 4 показано, как нагрузка P распределяется между спиральными пружинами. Если число витков выше приложенной точки нагрузки равно 6, а число витков ниже этой точки равно 5, то 255. Ответ.. t = 5: 6. 5.Такой же материал и такая же спиральная пружина 2 Круговое поперечное сечение и длина 256 собраны как показано на рисунке、
Он сжат между 2 параллельными плоскостями. Для 1,25 см и Р = 40 кг определите максимальное напряжение для каждой пружины. Рисунок 257. Решение. Из уравнения (162) следует, что нагрузка Р распределяется между силами, сжимающими внешнюю и внутреннюю пружины, то есть 3 пружины, которые обратно пропорциональны 3 квадратам радиуса витка. 7.5: обрабатывается как 10.Далее база Уравнение (161), максимальное напряжение этих * пружин составляет 185 кг / см *и 343 кг соответственно! будет ЦМГ.
Если допустимое напряжение равно[t 1 = 1300кг / см2], то какова максимальная нагрузка пружины в задаче 1?Каково удлинение пружины для этой максимальной нагрузки? * Ответ. 179 кг, 6 = 17,9 см. 7.Коническая пружина (рис.257) растягивается под действием осевой силы P.
Если допустимое напряжение[t] = 3000 кг / см2, диаметр поперечного сечения d = 2,5 см, радиус конуса в верхней части пружины # = 5 см, то безопасное значение P определяется в нижней части#8 = 20 см. Если число витков равно n, то определяется удлинение пружины Горизонтальная проекция центральной линии пружины представляет собой спираль, заданную следующим уравнением (Я-я) а 2 ТП Решение.
Для любой точки A оси пружины, определяемой значением угла a, расстояние от пружины bei равно максимальный крутящий момент при a = 2ll равен P/?2.Безопасный предел для Р, основанный на Формуле (161), равен: Соответствующий крутящий момент равен Пружина HES выводится из уравнения © (см. стр. 248). 8.It выполнен в тех же условиях, что и предыдущая задача, но сечение определяет требуемую площадь поперечного сечения катушки для квадратной конической пружины. Возьмем поправочный коэффициент, равный 1,09 (см. предыдущее задание). Ответ. 6 * » = 6 см *.
Смотрите также:
Предмет сопротивление материалов: сопромат
| Одновременное действие изгиба и кручения. Изгиб и кручение валов круглого поперечного сечения | Кручение полого вала |
| Энергия упругой деформации при растяжении | Вал прямоугольного поперечного сечения |

