Реакции на контур

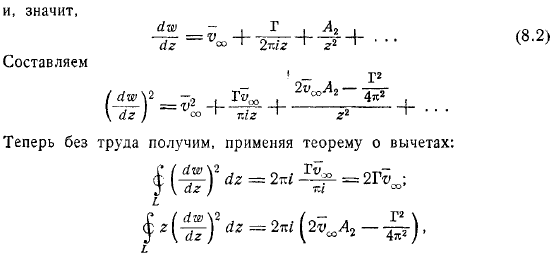
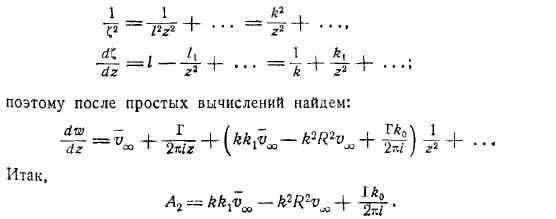
Реакции на контур

Генерал Чаплыгин сил, действующих на контур при протекании через контур с потенциалом – Начнем с Блазиуса чиновника. Поскольку функция является регулярной вне контура, интеграл предыдущей формулы может быть выполнен на любом контуре, который пересекает контур. Если вы в гидромеханике берете круг с плоскостью, центрированной в начале координат, которая содержит всю контурную линию внутри, вам нужно развернуть ряд рябины формы, потому что он бесконечен, а комплексная скорость равна.

Определите коэффициент метода конформного отображения , обратите внимание на следующую зависимость: есть преобразование в плоскости, и правая часть этих формул также одинаковы, поэтому мы строим их так, чтобы мы могли легко получить их с помощью теоремы остатка:по формуле, первая из этих формул уже известна формула, которая в настоящее время доказана в общем случае, формула нашего Кутта-Жуковского.

• Если обратить наше внимание на сопряженную величину, то есть сила, действующая на контур, равна произведению плотности, скорости циркуляции, скорости бесконечности, а ее направление получается из направления скорости бесконечности. Кромка, затем циркуляция, определяется по формуле и получается из формулы: чтобы определить момент возникновения силы, действующей на контур, достаточно найти коэффициент расширения комплексной скорости. Но если использовать формулу и значение коэффициента, то это выглядит так:. Итак, в результате несложных вычислений мы получаем.

Формула Чаплыгина — выражение для вектора подъемной силы, действующей на обтекаемый контур. Людмила Фирмаль

Итак, подставляя это значение в формулу, мы получаем: рассмотрим формулу конформного преобразования, где точка в плоскости с координатами называется конформным центроидом и называется конформным центроидом: поэтому, предполагая, что точка является центроидом контура, где распределена масса, элемент контура равен значению соответствующего, точка занимает контур в любом месте. Дуга окружности.

Таким образом, то же положение, что и последнее положение плоскости. Проведите прямую линию через точку под углом относительно оси и назовите ее критической или первой осью контура. Если поток параболы устойчивости бесконечности параллелен критической оси, то, согласно формуле, критическая ось также называется осью нулевого подъема, так как подъемная сила метода исчезает. Мы перепишем формулу, поскольку угол, то есть с учетом угла атаки к критическому отношению оси контура, так как сила, действующая на контур в этом случае изменяется пропорционально синусу угла атаки к критическому отношению оси контура.

• В формуле, заменить следующие значения для того момента, как я: как конформное центроидов попадает в точку, переместите контур в плоскости и назвать пункт тесно связан контур, обозначенный. В набросках, это может быть происхождение. Из предыдущей формулы находим выражение, не зависящее от угла атаки a для момента силы для фокуса. Имеется в виду следующая теорема Чаплина: давление, оказываемое на контур, можно свести к Жуковской силе, приложенной в фокусе, и паре с постоянной, то есть независимой. Угол атаки, момент.

Если поток вне обтекаемого контура свободен от вихрей и источников, то комплексный потенциал регулярен вне и по теореме Коши в формуле Чаплыгина контур можно заменить любым контуром, охватывающим обтекаемый профиль. Людмила Фирмаль