Оглавление:




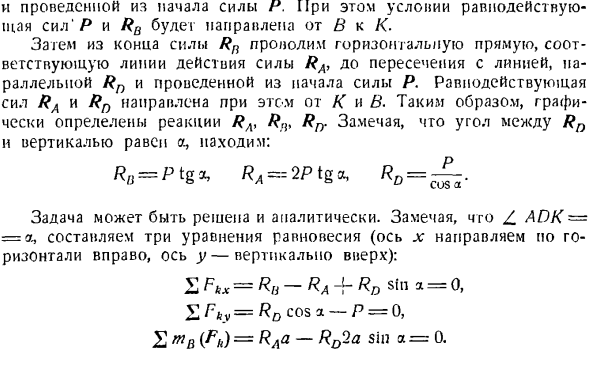
















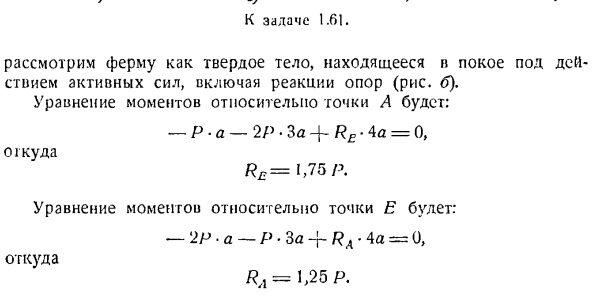
















Графическая статистика и методы расчета ферм
- Графическая статистика и методы расчета фермы 1°.Равновесие системы произвольных сил. Путь последователя и отличное дополнение. Если твердое тело под действием системы любой плоской силы также находится в равновесии, то такие силы можно определить из состояния равновесия путем последовательного сложения графически неизвестных values.
In кроме того, в системе сил, приложенных к 1 твердому телу, число неизвестных не должно превышать 3.В противном случае задача не определяется статически. По сравнению с аналитическим методом решения задачи равновесия системы плоских сил этот графический метод более очевиден, но его применение при большом количестве сил очень трудоемко.
Этот графический метод решения задачи рекомендуется применять, если общее число сил, действующих на твердое тело, невелико. Людмила Фирмаль
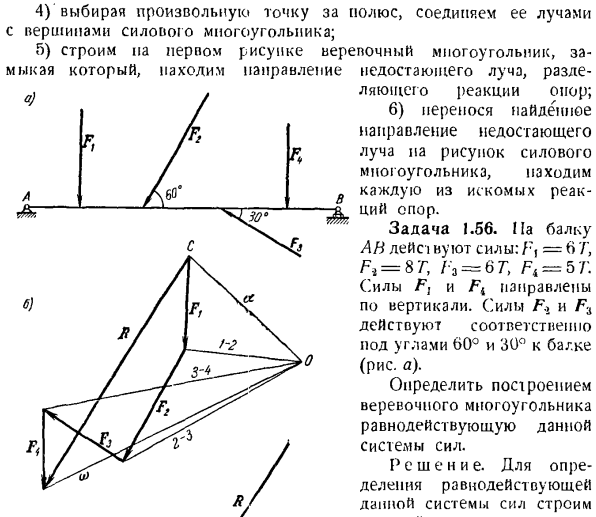
Метод добавления силы в ряд может быть применен к 2 версиям. Если под действием плоской системы заданной силы и 3 реакций твердое тело находится в равновесии, а его линии действия известны(/ j, / о,/ 3), то рекомендуется такая серия действий (1-й вариант): все известные силы получаются последовательно графически, и результат получается. 4) выделите любую точку полюсом и соедините ее с Лучом вершиной силового многоугольника. 5) на первом рисунке создайте веревочный многоугольник и закройте его.
Используйте это, чтобы найти направление недостающего луча и разделить его. Опора стержня, вызывающего реакцию; 6) Если вы перенесете направление найденного недостающего луча на форму силового многоугольника, то соответственно найдете нужную реакцию опоры. Задача 1.56. Луч ПА в ЛЕ с! Сила недействительна: F,= 6’/’, F%= ST,/ * s = 67, F4 = 5T. силы F и F {направлены вертикально. Сила F и Fs действуют под углом 00°и 30° с
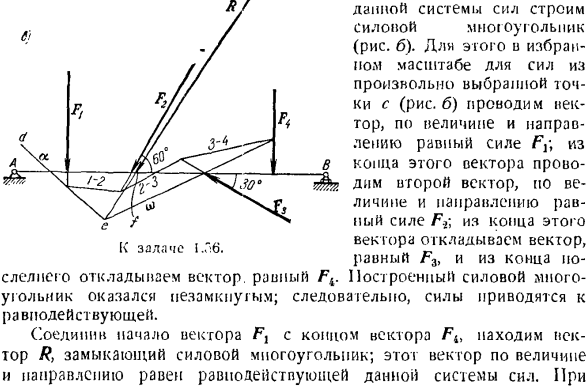
- Соответственно по отношению к балке (рисунок а). Создайте веревочные полигоны, чтобы определить исход этой системы сил. R s и я e. To определите последствия действия этой системы сил、 Постройте энергетический полигон этой энергосистемы (рисунок b).Для этого и выбранного масштаба силы из любой выбранной точки c (рисунок B) нарисуйте Тор, величина и направление которого равны силе F из кучи этого вектора.
Для этого вектора отложите вектор, равный F&, и отложите вектор, равный F {от последнего конца. Построенный энергетический полигон оказался открытым. Таким образом, сила сводится к результату. Если вы соедините его с конечной точкой вектора F4 в начальной точке вектора, вы найдете вектор R, который закрывает силовой полигон. Этот вектор величины и направления равен результату этой системы forces. So … Так… Если обойти силовой полигон, то все составляющие силы будут направлены в одну сторону, а вектор# — в противоположную.
Создайте канатный полигон, чтобы найти полученный объект point. Людмила Фирмаль
To сделайте это, нарисуйте Луч из произвольно выбранной точки O (рисунок B). в начале вектора Fh лучи 1-2 находятся в начале вектора Fb, лучи 2-3 находятся в начале вектора F2, лучи 3-4 находятся в начале вектора FK. Мы рисуем луч ω в конце вектора ФК.
Из любой точки d вблизи силы Fx (рисунок C) проведите прямую линию, параллельную Лучу a, проведите прямую линию, параллельную Лучу 7-2 от точки пересечения силы Fv, а из точки пересечения луча силы Z7 проведите линию, параллельную лучу силы F3 до точки пересечения нарисуйте прямую линию, параллельную лучам солнца.
Проведите прямую линию параллельную Лучу от точки пересечения луча 3-4 и линии действия силы Fi Продолжите линию, параллельную Лучу a, и проведите линию через точку e, параллельную вектору R, пока она не пересечется в точке e. точка пересечения между этой линией и Лучом выражается как a/.Это точка приложения Объединенных сил, приданных балке AB.
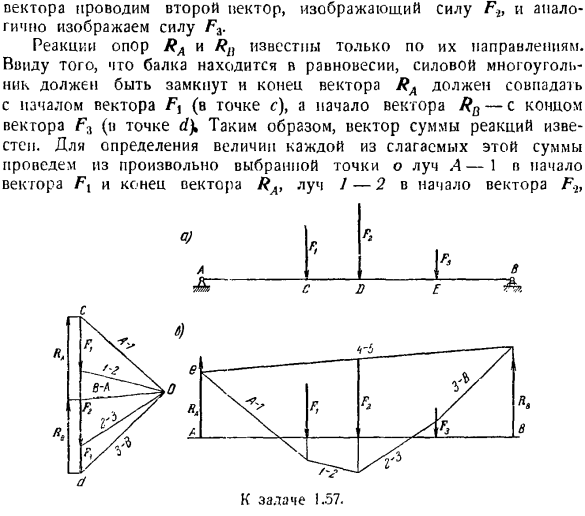
Используя выбранный масштаб путем измерения длины вектора R, найдите размер результата. 17.4 эквивалент к т. масштаб 1мм до 1/3 Т принят. Задача 1.57.Балка АВ длиной 12 м (рис. а) закреплена шариковым Кнупом с концом а, а конец В находится на опоре, прикрепленной к ролику. На балку были приложены следующие силы: Fi = 2 7, F. 2 = 3 7″, F $ = \T. расстояние: AC = 4 My CD = 2 Mt DE = 3m.
Создать веревочный многоугольник для определения реакции опоры A и B. Решение. Рассмотрим равновесие балки АВ. Активная сила действует на балку: Fu Fb F9.Применяя закон освобождения или связи, мысленно отбросьте опоры А и В и замените их действия реакциями. Реакция опоры B, которая прикреплена к ролику, направлена перпендикулярно плоскости, в которой расположен ролик, то есть вертикально вверх.
Вообще говоря, направление реакции шарнира а неизвестно, но ясно, что реакция шарнира а должна быть перпендикулярной, так как все силы, действующие на балку, направлены вертикально. Если эта реакция не вертикальная, то ее горизонтальная составляющая никак не сбалансирована, и равновесие луча невозможно.
Из вектора сила F. нарисуйте 2-й вектор, представляющий lt, и аналогично представьте силу Fz. Реакция поддержки RA и Rn известна только в ее направлении. Поскольку пучок находится в равновесии, необходимо замкнуть силовой многоугольник и сопоставить конечную точку вектора RA с начальной точкой вектора fi (точка c) и начальную точку вектора RD с конечной точкой вектора f3 (точка tf).
Известно reaction. To определите значение каждого из членов этой суммы, от произвольно выбранной точки Луча A-1 до начала вектора Fj и до конца вектора RA, от Луча 1-2 до вектора F. проведите его до начала. л. о.) Так… Д. И Е. Один. И д. К выпуску 1.57. е. \ От Луча 2-3 до начала вектора F3) от Луча 3-B до начала вектора RB(совпадает с концом вектора в точке d).Направление пучка B — / 1 неизвестно, поскольку неизвестны размеры реакций RA и RB.
Далее приступаем к постройке канатного полигона. Для этого из точки е на линии действия реакции RA (рисунок C) проведите прямую линию, параллельную Лучу A -/, из точки пересечения к точке пересечения с действием силы Fu, к точке пересечения с Лучом/-2, проведите прямую линию, параллельную лучу действия/ 7.; Аналогично проведите прямую линию, параллельную Лучу 2-3u 3-B, пока он не пересечется с рабочими линиями силы F3 и реактивной силы RB.
Поскольку система сил находится в состоянии равновесия, необходимо замкнуть многоугольник каната. Таким образом, линия между линиями действия реакции RA и RB должна проходить через точку e. он делит отрезок dc на отрезки, равные реакции Ra и Rb(для наглядности на рис.6 реакции RA и RB немного перемешаны слева).Если вы измерите значения реакции, найденные на принятой шкале, вы найдете эти значения: RAz = 3,\ T, RB = 2.9 7 *.
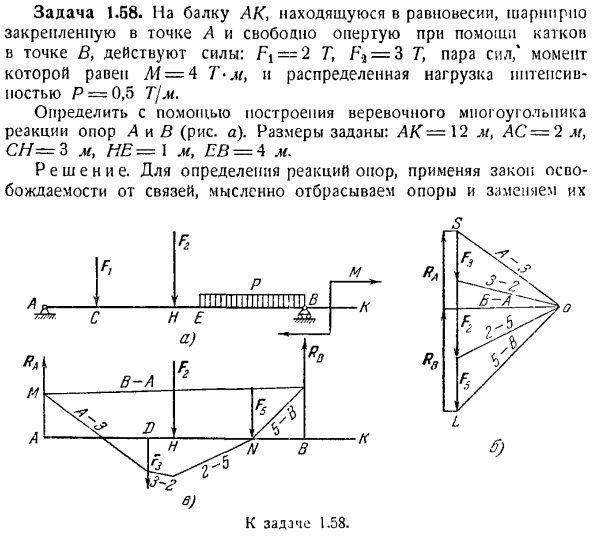
Задача 1.58.In в случае балок АК, находящихся в равновесии, закрепленных в точке А и свободно поддерживаемых роликом в точке Б, действует сила: F -2 T, t \ = 3 T, пара / момент силы составляет M = 4, распределение веса нагруженного нитепсиса.- Кость Р = 0,5 т / л *. Используя конструкцию канатного полигона, определите реакцию опор а и в(рисунок а).Размеры следующие: АК-12 М, АС-2 м, СИ = 3 г, Не-И Л/, и£= 4 г. The solution. To определите реакцию поддержки, примените законы, которые™освободил от связи, и мысленно отбросьте и обменяйте поддержку
К выпуску 1.58. ф Воздействие на луч осуществляется реакцией поддержки ядерного оружия и РБ(рисунок в).Поскольку все активные силы направлены вертикально вниз, а сумма проекций сил попарно для любой оси равна нулю, обе реакции направлены вертикально вверх. Действие пары сил не изменяется, поэтому она переносится в любое место на плоскости, не меняя момента пары, заменяя пару силой Fi и F, а абсолютное значение составляет 2 т, соответственно, на расстоянии 2 м. приложите к точкам
C и A равное 2 т и приложите к точке это уравновешенно и не будет рассматриваться в дальнейшем. Для решения задачи с использованием канатного полигона необходимо заменить распределенную нагрузку концентрацией F. модуль этой мощности Fs = P * EB = 0.5 * 4 = 2 G, приложенный к средней точке L / сегмента EB. Приступайте к построению сил polygons. To сделайте это, отложив вектор на выбранном масштабе от любой точки 6 «(рисунок Б), но модуль и направление будут равны
силе F3. ФЗ. Поскольку пучок находится в равновесии, силовой полигон должен быть замкнут, поэтому начало вектора, соответствующего реакции Rf {), должно совпадать с концом вектора, соответствующего силе Fr, и началом вектора, соответствующего силе реакции: RA>точка I-это точка I. Для наглядности нарисуйте Rls и RA (рисунок b) немного левее. Затем нарисуйте луч A-3 из любой точки o в начало вектора F3 и Луч 3-2 в начало вектора Fb 2 — <5 в начало вектора F3l луч B-A не может быть
нарисован в начале вектора Rw, но поскольку коэффициенты силы RB и RA неизвестны, вектор рисуется в начале вектора Fb. Далее приступаем к постройке каната Polygon. To для этого проведите прямую линию, параллельную лучу а-<3 от любой точки М по линии действия реактивной силы RA (рисунок с), пока она не пересечется с линией действия силы F3.От пересечения проведите прямую линию, параллельную лучам 3-2 и пересекитес
ь с линией действия силы F. от пересечения лучи 2-.Проведите прямую линию, параллельную 5 и от пересечения до пересечения с линией действия силы. Параллельно балке 5-B, перед пересечением линии действия c *и силы RlV, необходимо замкнуть канатный многоугольник, поскольку рассматриваемая система сил находится в точке равноденствия. Таким образом, линии между линиями действия сил Rl {и RA являются
Пройдите через точку L /в направлении силы L (рисунок b).Теперь вы можете нарисовать луч B-A, параллельный этой линии из точки o (рисунок B).Этот пучок делит отрезок SL на вектор, равный реакции RA и Ri}.Если мы измерим эти векторы и умножим их на выбранный масштаб, то увидим, что = 3.9 T, a = 3.1 T. Задача 1.59.Балка АВ, которая закрепле
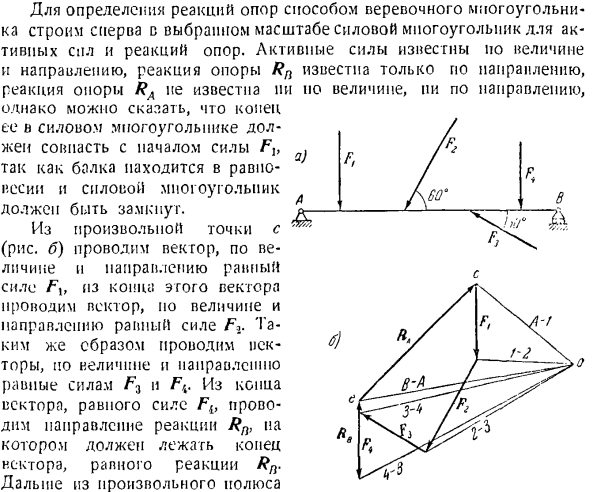
на шарниром в точке А и поддерживается с помощью ролика в точке Б, направлена вертикально: сила Fi = 6 т, f1 = 8 т, f7 = 6 т, — O T1, сила F {и Fi. Силы Fch и Fz направлены на балку под углами 60°и 30°соответственно. Создайте канатный полигон для определения отклика опоры (рисунок а). The solution. To определяя реакцию поддержки, мы применяем закон Бонда прощения, мысленно отбрасывая поддержку, заменяя ее действия реакцией РА и РБ. Поскольку опора B прикреплена к ролику, реакция Rn вертикально направлена вверх, что не препятствует
движению вдоль плоскости, в которой расположен ролик. Шарнир реакция РА-это любое направление прицелов. л.) 2) найти пересечение результирующей линии действия и 1 линии действия (/j) реакции. 3) перенесите результат в эту точку и разберите его на 2 силы.1 направлена вдоль линии f, а другая 1 направлена к пересечению рабочих линий других
2 реакций(/ 2, / 3). 4) составляющая результирующей эффективной силы, ориентированная вдоль линии/ ’ определяет величину начальной реакции 5) переместить 2-ю составляющую синтезированной активной силы в точку пересечения линий действия остальных 2 реакций n и развернуть в направлении действия nx(/ *и / 3).Найдите нужное значение последних 2 реакций. Под действием плоской системы заданной силы и 2 реакций твердое тело находится в состоянии равновесия, для 1 реакции известна только точка приложения(а), а для 2-Эт
а последовательность действий рекомендуется (2 ВАР и муравей). ): 1) непрерывно графически складываем все известные эффективные силы и получаем результат. 2) перенести результат в точку пересечения (/2) с линией действия второй реакции с ее линией действия (/2). 3)на пересечении разложите результат на 2 компонента: 1-вдоль линии действия 2-й реакции, другой 1-по направлению к точке А, 1-й компонент определяет 2-
ю реакцию, а 2-й компонент определяет величину и направление реакции в точке А. Задача 1.55. Перпендикулярный и гладкий гладкий стержень CD, весящий P, расположен в точках A и B (рисунок A) на цилиндрических шарнирах, а на гладкой плоскости, наклоненной к горизонту под углом a, имеется КС D. В случае AB = AD = a реакция в точках A, B, D определяется графически. Чтобы определить реакцию опоры с помощью метода канатного полигона, сначала создайте активную силу опоры и полигон силы реакции в выбранном масштабе. Активная сила известна по величине и направлению, реакция опоры Rn известна только по направлению, реакция опоры RA неизвестна по величине и направлению pi, но конец силового полигона не известен. Жена совпадает с началом действия силы Flf, потому что луч находится в ра
вновесии и необходимо закрыть силовой многоугольник. Из любой точки c (рисунок B) нарисуйте вектор равной величины и направления силы Fx, а с края этого вектора нарисуйте вектор величины и направления, равный силе F. аналогично нарисуйте вектор, но величина и направление равны силам F :)и F {.От конца вектора, равного силе Flt, оттягивается направление реакции Rn, где расположен конец вектора, равный реакции Rn. Далеко от любых полюсов Луч-1 на начало вектора Ф, Рэй / −2 до начала работы с векторной графикой Рэй 2-3 до начала вектор, пригодный Ф3>Рэй 3-4 1 к началу вектора, Луча, 4-Б в начало ве
ктора R/?Луч B-A не может быть нарисован в начале вектора RA, потому что размер реакции Rn неизвестен. Чтобы определить величину реакции Rl}, приступаем к построению каната Polygon. To для этого проведите прямую линию, параллельную Лучу A-I через точку A (рисунок 0) (так как это единственная известная точка на линии действия реакции RA), пока она не пересечет линию действия силы Z7.Через эту точку пересечения проведите прямую линию, параллельную Лучу/-2, пока она не пересечет линию действия силы/ \ 2.Через эту точку пересечения пр
оведите прямую линию, параллельную лучам 2-3, пока они не пересекут линию действия силы F2.Аналогично проведите прямые линии, параллельные лучам 3-4 и 4-Б, пока они не пересекутся с линиями действия сил F4 и Ru. Прямая линия, параллельная лучу 4-B, является точкой (I. В связи с тем, что канатный полигон должен быть закрыт, когда система находится в равновесии, точка d соединяется с точкой A, где начинается
построение канатного полигона. Теперь можно провести луч B-A через полюс o параллельно прямой dA (рисунок B).Лучи B-A пересекают направление реакции Rn в точке e, определяющей конечную точку вектора RB. Если соединить конец вектора RB с началом вектора Ft, то можно найти размер и направление реакции RA. By измерение сегментов, которые нарисовали реакцию
И. Я. И. м — ’2Н-3. Количество стержней: то есть, если вы удовлетворяете этому уравнению, можно рассмотреть 2 случая. 2/7 −3.、 В этом случае ферма статически неопределима. Т <2л-3 Конструкция не меняется геометрически, но выигрывает и приобретает подвижность(становится механизмом). Дж Расчет сил стержней ферм с использованием статических методов (в том числе графостатики) может быть выполнен только для статически определенных ферм*). Расчет фермы, которая не может быть определена статически, выходит за рамки теоретической механики, так как необходимо учитывать структурн
ые деформации. В дальнейшем будем считать, что данная активная сила приложена к узлам фермы, они находятся в той же плоскости, что и ферма, и поле зрения не зависит. В этих условиях стержень сжимается или растягивается, поэтому реакция стержня совпадает со стержнем в направлении. Статически определяемая ферма вычисляется одним из следующих 3 способов: а) как отключить узел. б) построение диаграммы Максвелла-Кремоны、 в) по методу сечения. Расчет позволит определить усилие стержня фермы. Активные силы и реакции опоры являютс
я внешними силами по всей ферме и считаются твердыми. Сила стержня в этом случае-внутренняя сила. Поэтому для определения усилия необходимо, согласно общим правилам, учитывать равновесие тех частей фермы, где необходимым усилием является внешняя сила. Аналитические и графические методы можно использовать при расчете фермы с помощью метода, отключающего узлы. Решая задачи с расчетом фермы с помощью метода разъединения узлов аналитическим методом, необходимо выполнить первые 4 пункта, которые указаны в н
ачале книги на стр. 15. 5) Определите реакцию опоры, используя уравнение равновесия всей фермы, которая считается сплошной, или используя канатные полигоны. 6)2 стержня разрезают узлы для сближения и считают равновесие под действием активной силы и реакции стержней на разъединение. Определите эти реакции из 2 уравнений проекции сил, приложенных к узлам на декартовых координатных осях. 7) переходите от узла к узлу и рассматривайте равновесие каждого узла как well. In в этом случае каждый узел имеет только 2 неизвестные силы на стержне
. Для каждого узла создайте 2 уравнения равновесия в проекции осей x и y, чтобы определить все силы, необходимые для стержня. В графическом виде для решения задач вычислительной фермы путем разъединения узлов необходимо выполнить первые 4 пункта, перечисленные в начале книги. 15.После этого: 5) Определите реакцию опоры, используя уравнение равновесия всей фермы, которая считается сплошной, или используя канатные полигоны. 6) 2 стержня разрезаемого узла сходятся, учитывая его равновесие под действием заданной активной силы и реакцию разрезаемого стержня. Определите эти реакции, пос
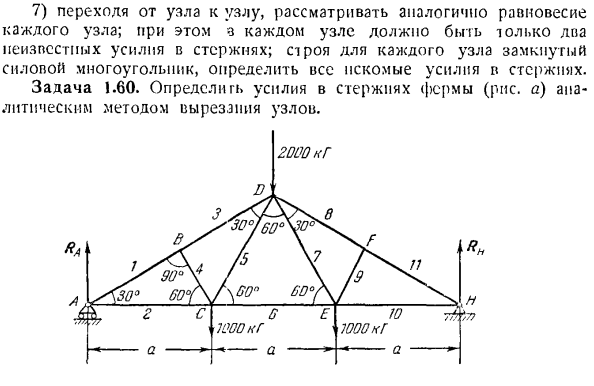
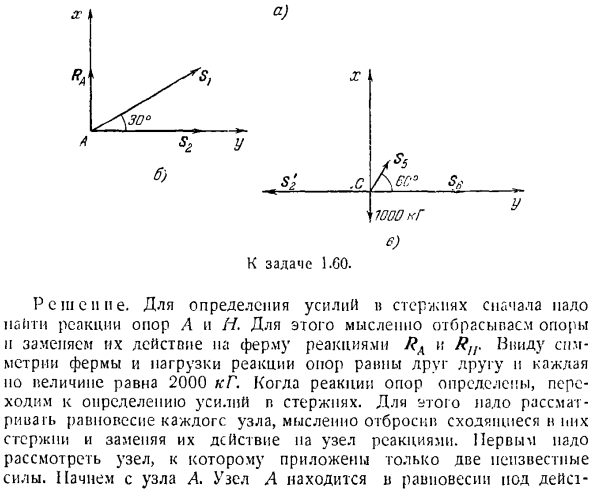
троив замкнутый треугольник или многоугольник сил, приложенных к узлу. 7) переходите от узла к узлу и рассматривайте равновесие каждого узла в одном и том же way. In в этом случае каждый узел имеет только 2 неизвестные силы на стержне. Постройте замкнутый силовой полигон на каждом узле и определите все необходимые силы на стержне. Задача 1.60.Аналитический метод нарезания Сучков позволяет определить усилие на стержне фермы (рисунок а). Ее. ИКС А% V б> СЖ. С AL * b Ву-г-г К задаче 1.60. The solution. To определив силу тяги, необходимо сначала найти с
илы реакции опоры А и Н. для этого мысленно выберите опору опоры, а действие в трузиону? Когда противодействие опоры определено, приступают к определению силы в стержне. По этой причине мы рассматривали равновесие каждого узла, мысленно отбрасывая сходящиеся на них стержни и заменяя действие на узле реакцией. Первое, что нужно рассмотреть, — это узел, в котором применяются только 2 неизвестные силы. Начнем с узла А. узел а、 е.) Известными реакциями РА и неизвестных реакций стержней Г и 2.Обозначим реакцию стержней (соответственно, на рисунке Б) и выведем их из узлов. Поэтому будем считать, чт
о стержень растянут. Затем проведите ось l *через точку A и составьте систему уравнений равновесия узла A. сумма проекций всех сил на эти оси равна нулю. Проекционные уравнения для осей jc и y выглядят следующим образом: + cos 30°= 0, Ra + Sx cos 60°= 0 Я найду тебя отсюда.: = −4000 кг,= 3404 кг. Отрицательное значение реакции S1 фактически направлено в противоположную сторону, и стержень Y не растягивается, как ожидалось, что указывает на то, что еж r растянут. Теперь вернемся к изучению равновесия узлов B. In узел B, 3 стержня сходятся, из кото
рых 3 стержня / и 3 соединены вдоль 1 Прямой линии, а 4 стержня наклонены против them. No активная сила приложена к узлу B. As в результате эструс В находится в равновесии с йодом за счет действия 3 стержневых реакций. Э / о возможен только в том случае, если сила тяги 4 равна силе пули. Это объясняется тем, что он проецируется только в направлении, перпендикулярном стержню 4.
Возврат в узел С. узел С находится в равновесии под действием 2 неизвестных реакций, причем известная реакция S’ir равна по величине активной силе Sc, G до 1000, а реакция S, приложенная к узлу а, направлена в противоположную сторону(рис. с).Нарисуйте координатные оси через точку C и добавьте уравнения равновесия узла C. уравнения проекции на оси jc и y выглядят следующим образом: — SH — ^ cos 60° — pbe = 0, Si cos 30°-1000 = 0 Я найду тебя отсюда.: = 1155 кгр ^ = 2886,5 кг.
В результате стержни 5 и 6 находятся в заточении, как и ожидалось. Полная симметрия (достаточно определить мощность стержня в левой половине фермы с точки зрения вяза и / или применяемого в узлах оборудования); например, силы стержней 1 и Y, 2 и 10 равны по симметрии. Задача 1.61.Вырежьте узлы и графически определите работу пермской фермы (рисунок а) на ферме. E с PE в neck. To определить реакцию в точках A, B, D, рассмотреть равновесие стержня CD. На стержень па действует 1 активная сила-сила тяжести Р, направленная вдоль стержня.
Стержень находится в равновесии под действием 4 сил: веса P, реакции наклонной плоскости и цилиндрических соединений A и B. используя закон освобождения от связи, мысленно отбросьте связь и замените действие на стержень реакцией(рисунок B). Реакция гладкой наклонной плоскости R приложена в точке D и направлена перпендикулярно наклонной плоскости. Поскольку такой шарнир не препятствует движению вдоль оси, противодействие цилиндрического шарнира направлено
перпендикулярно оси шарнира. Эти реакции называются RA и RB (рисунок B).Таким образом, стержень CD находится в равновесии как свободное твердое тело с 4 действующими силами: P, RA, Rfi, Rfy Продлите линии действия реакций RA и Rn до тех пор, пока они не пересекутся в точке K(рисунок B).Пройдите через линию действия 2 сил с равными эффектами! Проходя через пятно
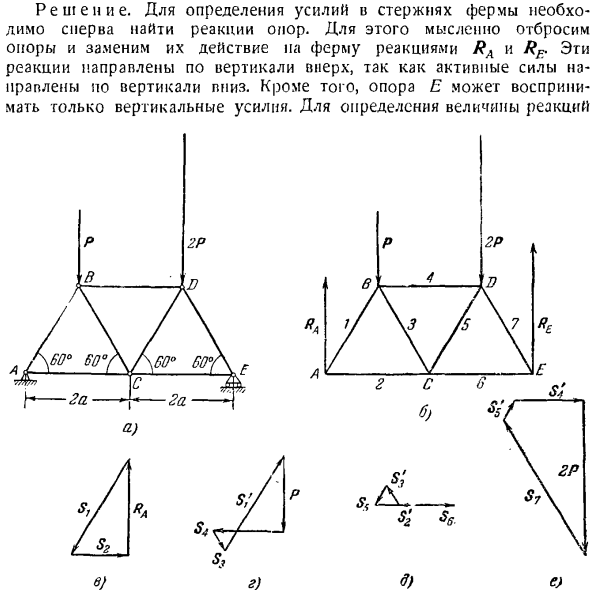
K-другие 2 мощности P и Rl{ The solution. To определите силу ферменной конструкции и штанги, вы должны сперва найти реакцию support. To сделайте это, мысленно откажитесь от поддержки и замените воздействие на ферму реакцией РА и РФ. Эти реакции направлены вертикально вверх, так как активная сила направлена вертикально downwards. In кроме того, опора Е может принимать только вертикальную силу. Как определить размер реакции Так… К задаче 1.61. Рассмотрим
ферму как покоящееся твердое тело под действием комбинации активных сил, включая реакцию опоры (рисунок б).Уравнение момента для точки A имеет вид: -П•а-2Р * б + р£ * 4а = 0、 Откуда? Я£= 1.75 Р. Уравнение момента для точки E имеет вид: −2Р•а-Р-За+ Ра•4а=О、 Откуда? Ял = 1,25 П. После определения реакции опоры, затем найти силу стержня. Стержень обозначается цифрами 7, 2, 5, 7. Сначала вырезают узел, в котором действуют только 2 неизвестные силы, например, узел L. 3 силы прикладываются к узлу A. RA опорная реакция, s-резка по реакции, стержень 7
.Его размер неизвестен. Напомним, что если оба конца прямого стержня закреплены шарнирами, а все силы приложены только к узлам, то совпадение направления стержня и реакции наблюдается всегда. Чтобы определить величину реакции стержней, постройте треугольник сил и отложите их в сторону в том порядке, в котором они возникают при повороте узлов по часовой стрелке. Первое место в шкале занимает известное значение RA (рисунок O).Начиная с его конца, проведите прямую линию, параллельную стержням 7 и 2, пока они не пересекутся на стержнях 7 и 2
.Стороны полученного треугольника реагируют S и S. 2. определите, чтобы найти их направление, переместите вокруг треугольника силы в направлении, указанном известной силой RA. Когда узел находится в сбалансированном состоянии, стрелки замкнутого силового полигона перемещаются в одном направлении. Если переместить реакцию Si на стержень 7, то можно увидеть, что стержень 7 сжат, потому что он направлен к участку. Реакция S. Если переместить 2 на стержень 2, то можно увидеть, что это реакция из узла A. Таким образом, стержень 2 растягивается. З
атем отключите узел I. 4 прилагаются усилия.2 неизвестные реакции » стержень-3 и-4, 53 и-S4, стержень — / известные реакции. Активная сила R. вы создаете полигоны для этих сил. Сначала поместите силу Sj на шкале (рисунок D), добавьте активную силу P к ее концу, а затем проведите прямую линию, параллельную стержню 4 через конец силы P, и прямую линию, параллельную стержню 3 через начало силы S. Стороны полученного прямоугольника определяют реакцию Sz. To найдя их направление, мы движе
мся по квадрату в направлении, указанном известными силами. Если мы передадим ответ 5H на стержень 3, мы увидим, что он ориентирован от узла B, и в результате стержень 3 растягивается. Перенаправление реакции Sk от стержня 4 направляется к узлу B, поэтому стержень 4 сжимается. Затем разрезают узел C. 4 прилагаются усилия.2 неизвестные реакции и 56 стержней 5 и B, и 2 известные реакционные стержни 2 и 3, равные реакциям 53 и Sb
Пока они не пересеклись. Если мы переместим многоугольник полученной силы в направлении, указанном известными силами, мы увидим направление реакции S и S. Если вы переместите реакцию 53 на стержень<5, стержень 5 сжимается, потому что он направлен в узел C. Если вы перенесете реакцию$ 6 на стержень 6, вы увидите, что стержень 6 растягивается, потому что он выводится из узла C. Затем к разрезанному узлу D. прилагаются 4 силы: стержень 7, неизвестная сила реакции 1, активн
ая сила 2P, а также реакция, приложенная к узлам B и C соответственно и известная реакция, равная Ss, направленная в противоположную сторону (обозначается S) ^и далее строится силовой многоугольник. Сначала отложите силу S^(рисунок RAy =1.5 P коэффициент реакции шарнира a равен РА = ВР * х-я-1.8 П. Определите направление реакции поддержки
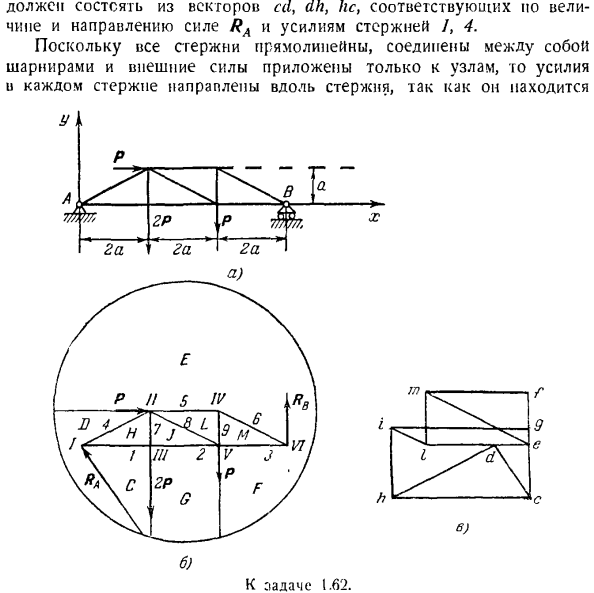
Изобразите все внешние силы, приложенные к ферме, включая реакцию опоры, так, чтобы ее вектор располагался вне контура фермы(рисунок Б).Линия действия фермы и внешней силы обозначается буквами C, D, E, F, Cg, а плоскость, заключенная в стержень фермы, обозначается буквой I,/,/., Обозначенные буквой M, узлы фермы обозначены римскими
цифрами/,//, IV, V, V /;стержни обозначены арабскими цифрами/ — 9. Сначала мы построим многоугольник внешних сил (рисунок C).Это связано с тем, что ферма находится в состоянии равновесия, она должна быть закрыта. Выделите силы в том порядке, в котором они будут встречаться при перемещении фермы по часовой стрелке, а при перемещении фермы по часовой стрелке укажите 2 маленькие буквы, соответствующие этим большим буквам, обозначив 2 смежные области, разделенные линией действия этой силы. Постройте на шкале вектор cd, соответствующий
силе реакции RA, добавьте к нему вектор de, соответствующий силе P, а также отложите векторы ef, fg и gc, соответствующие силам Rn, P, 2P. Внешняя сила, приложенная к узлам фермы, начинает строить полигон, потому что он получил замкнутый полигон. Например, из узла I начните с узла только с 2 неизвестными силами. Построить многоугольник, обойти узлы по часовой стрелке, указать мощность стержня 2 с маленькой буквы, соотве
тствующей заглавной, обозначив нижние смежные области, разделенные этим стержнем. Согласно принятой нотации, мышца-прямоугольник силы, приложенной к узлу I Sekayugsya б. Таким образом, рабочая линия их результата проходит через точку В. Таким образом, все силы, действующие на стержень CD, сводятся к 2 силам, 1 К K вдоль линии действия, а еще 1 к B. So, эти силы направлены в противоположном направлении вдоль 1 Прямой VK. Величина и направление, как известно, заставляют R. откладывать в выбранном масштабе (рисунок C). И Задача 1.55. Он состоит из вектора величины и направления
, соответствующего силе РА и силе стержня. Все стержни прямые, соединены между собой шарнирами, и сила каждого стержня направлена вдоль стержня, так как только узлы подвергаются внешним воздействиям. Задача 1. до 62. И 2 силы, равновесные под действием только реакции суставов. Удилище в этих условиях является только ежиком или растяжкой. Вектор cd на рисунке уже есть exists. To найдите вектор dh и его
, достаточно пройти прямую линию / точку c, параллельную стержню, и прямую линию d, параллельную стержню 4, и поместить букву Jl в точке их пересечения. /// Перейти к узлу. Полигон приложенных сил должен состоять из векторов gr, ch, hi, ig. Вектор gc, ch на рисунке уже существует. достаточно провести прямую линию, параллельную стержню 7 через векторы igi hi, ig, точку h, и прямую, параллельную стержню 2 через точку 2, и поместить букву L в точке их пересечения. Перейти к узлу//.Многоугольник приложенных к нему сил должен состоять из векторов lh, hd, de, el, 11.Ф
игура Wekgor lh, hd, de уже exists. So, колышек растительного масла el, и проведите прямую линию, параллельную стержню<5 Через точку e, и прямую линию, параллельную стержню 8 через точку i, и поместите точку/на ее пересечении. Передать его на узел В. полигона мощности, подводимой к нему, должен состоять из векторов ФГ, ги, Ир, лм, МФ. Векторы fg, gi и il на рисунке уже exist. To найдите вектор lm, mf, проведите линию, параллельную точке / стержню 9, а точку/-прямую линию, параллельную стержню 3, По
местите букву/; /в точке пересечения. Силовой полигон, приложенный к узлу IV, должен состоять из векторов ml, le и art. Вектор ml, le, на рисунке уже exists. To найдите вектор cm, соедините точки m и C напрямую. Поскольку вектор em соответствует силе и стержню 6, эта линия должна быть параллельна стержню 6.Таким образом, параллельность этого вектора и стержня 6 является проверкой правильности построения диаграммы. Если мы посмотрим на узел VI, то многоугольник приложен
ных к нему сил должен представлять собой совокупность векторов fm, mc и ef, которые уже представлены на рисунке. Таким образом, остается только выяснить все усилия 9 стержней, определить, какие стержни натянуты, а какие нет compressed. To для этого мысленно перенесите вектор силовых полигонов каждого узла на соответствующий стержень и определите их направление. Если вы идете к рассматриваемому узлу, стержень будет сжат при растяжении от узла. Силовой полиго
н cdh характеризует равновесие узла 1.Силы этого треугольника направлены от c К d, от d К h и от h к c. таким образом, вектор dh направлен к узлу/.Это означает, что стержень 4 сжат. Он узел / вектор направлен от. Это означает, что стержень 1 растянут. Четырехугольная гчи силы / / / характеризует равновесие узла. Власть эта площадь от G до G, G на h}, h в г
Для этого создайте 3 уравнения равновесия или примените веревочно-полигональный метод. 2) мысленно ферму, к которой приложены все внешние силы, разрезают на 2 части так, чтобы число отрезанных стержней не превышало 3, а при эксплуатации отброшенных частей предполагается, что все стержни растягиваются и заменяются с требуемым усилием стержня.; 3) Создайте уравнение равновесия для части фермы так, чтобы каждое неизвестное уравнение содержало 1 неизвестную
силу. Для этого мы создадим уравнение момента относительно точки пересечения линий действия 2 неизвестных сил. Если 2 стержня параллельны, создайте уравнение проекции на оси, перпендикулярной этим стержням. Это также включает в себя 1 неизвестную силу. 4) Если вы решите каждое составленное уравнение, вы найдете необходимую силу для стержня. Если ответом будет знак минус, это означает, что стержень сжат, но не растянут. Задача 1.63.Определите усилие стержня фермы методом сечения (рисунок а). The solution. To определите усилие штанги ферменной конструкции, вы должны сперва опре
делить противодействие support. To сделайте это, мысленно откажитесь от поддержки Ферма как твердое тело находится в равновесии под действием 7 активных сил и 2 неизвестных реакций опоры. Благодаря симметрии фермы и нагрузки, реакция опор равна друг другу, а размер каждой составляет 6А После определения реакции опоры приступают к определению силы тяги фермы. Мы мысленно срезали ферму к удочке. Например, нужно определить из стержней 8, 9, 10 работу (рисунок Б), а затем снять правую сторону фермы и заменить действие стержня реакцией С. Вырежьте стержни из узлов и / или п
редположите, что стержни 8, 9 и 10 растянуты. Левая сторона фермы(рисунок B) Реакция активной силы опоры RA> 3 и реакция стержня S8) находится в равновесном состоянии при SJ0.To найдите размер этих реакций, создайте уравнения равновесия на левой стороне фермы. Это сделает сумму моментов всех сил равной нулю по отношению к точкам/и L, где пересекаются линии действия 2 неизвестных и неизвестных сил. По этой причине уравнение момента содержит только 1 неизвестный. Следовательно, уравнение момента для точки / равно: Ра. 2а-Р•2А-2
Р•а-F СГ•а = О.、 Откуда? $ п= — № Отрицательное значение величины реакции, по сути, указывает на то, что стержень 8 сжат, так как эта реакция направлена в направлении, противоположном принятому, то есть к узлу E. уравнение момента для точки L имеет вид: −2Р-а-2Р-2а-Р-За•Ф — РА•3а-Sl0•а=О、 Откуда? = ОПЕРАЦИЯ. Как и ожидалось, ядро JO было расширено. Так как силы SH и S, rt параллельны, то на их пересечении отсутствует эструс. Таким образом, вместо уравнения момента мы строим уравнение проекции для всех сил на вертикальную ось, перпендикулярную стержням 8 и JO-для определения силы. РА-Р-2л-2П
в COS 45°= О、 Откуда? Отрицательное значение реакции серы, по сути, направление, противоположное направлению, в котором используется реакция, т. е. направлено к узловой точке l, указывая на то, что стержень 9が圧 圧縮されること 。す。Аналогично, сила может быть определена методом поперечного сечения стержня этой фермы. Чтобы овладеть навыками решения задач, необходимо знать, как решать задачи с помощью И. В. Мещерского из сборника задач теоретической механики издания с 1950 года рекомендует решать следующие задачи:199、202、204、205、206、207 。 При этом условии равнодействующая сил Р и RB направлены от B до K. Затем от конца силы Rn проведите го
ризонтальную линию, соответствующую линии действия силы Ra, пересекая линию, параллельную силе R, и от начала силы P до чертежа. Результирующие мощности Ra и Rn направлены от K и B. l, Rn. Заметив, что угол между Rn и вертикальной линией равен a, мы видим, что: Р, = р ТГО, Ра-ИС ТГА, РД =〜 Задача может быть решена аналитически. Заметим, что Z AIC = = a, составляют 3 уравнения равновесий(ось l; горизонтально вправо, ось y-вертикально вверх): 2Fk * = ра-ра + РД грех = о、 В Fby = РД, потому что а-Х = 0,£ТВ(FН)= Раа-RD2a грех = 0 Для овладения на
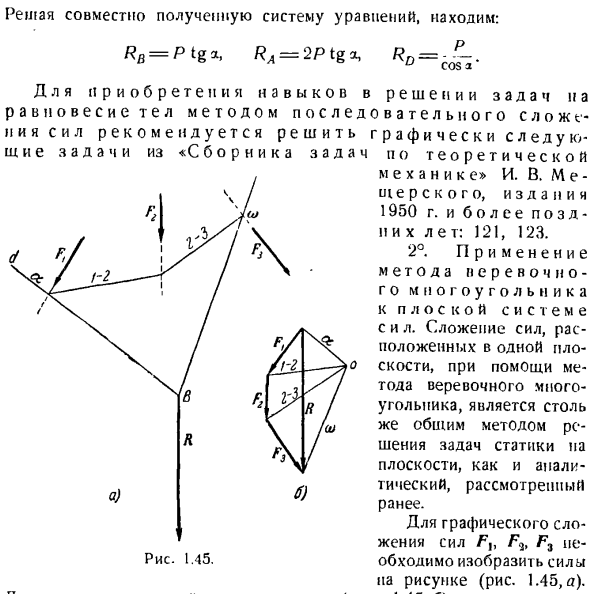
выками решения задач с равновесием в организме методом непрерывного сложения сил рекомендуется графически решать следующие задачи из «сборника теорий». Механиксвилл. В. М Е- 1ч / Терский, издание sJoj 1950 и др. 2°.Применение канатного полигонального метода для силовых плоских систем. Использование метода канатных полигонов для сложения
сил, расположенных в одной плоскости, является распространенным способом решения статических задач на плоскости, как и в случае ранее рассмотренных аналитических задач. Сила F. Для добавления J графики, F3 составляет 1.45.Кинематографические способности Рисунок (рисунок 1.45, a). Если решить систему уравнений, полученных совместно, то получим RB = P tgo, Ra =2Ptg a,=.
Далее построим силовой полигон (рис. 1.45.6), и первая сила Fl, за исключением любой точки? Вы также можете использовать его головы отсвоего вектора FT и ее главный вектор КТ от вектора Ф3.Начало Первой силы связано конем и вектором I последней силы. Вектор R определяет величину и направление результата. Чтобы найти линию действия, возникающую из нее, Выберите любую точку O позади полюса и соедините начал
о и конец каждой силы с прямой линией, называемой полюсом и Лучом. Первый луч обозначается а, а Луч обозначается w от конца первой силы до начала Второй, до последнего луча, например, 1-2. Далее (Рис.1.45, а) проведите прямую линию от любой точки d, параллельной Лучу i, до пересечен
ия с линией действия силы Flt; от этой точки проведите прямую линию, параллельную Лучу 1-2, до пересечения силы Ft с линией действия; от этой точки проведите прямую линию. Прежде чем пересечь линию действия последней силы Fv, проведите прямую линию, параллельную Лучу 2-6 от этой точки, параллельную Лучу w. затем продолжайте полученные лучи a и w до пересечения в точке B, что составляет 1 точку на линии действия результата. Перемещая найденный вектор из многоугольни
ка сил в точку B, можно считать задачу нахождения результирующей системы сил решаемой-Flt Fit F3. 1. 45 построенная поверх рисунка пунктирная линия называется канатным многоугольником. Это решение может быть применено к любому количеству сил в одной плоскости. Если система сил находится в равновесии, то силовые полигоны и канатные полигоны должны быть closed. So, рис. 1.45, конец последней силы должен сов
падать с началом Первой силы. Рис. 1.45, а лучи a и w должны быть направлены по прямой линии. Если силовой полигон замкнут, а канатный полигон не замкнут, то силовая система сводится к паре forces. In в этом случае в силовом полигоне лучи a и w сливаются в 1 прямую линию, а в канатном полигоне лучи a и w параллельны друг другу. Для решения задачи определения составной плоской системы сил методом канатного полигона рекомендуется следующая последовательность действий: 1) Нарисуйте твердое тело с приложенной силой, в выбранно
м масштабе рисунка. 2) Создайте силовые полигоны по отдельности и найдите их замыкание R\ 3) выделите любую точку полюсами и соедините ее с вершиной силового многоугольника прямой линией-лучами, обозначенными а, 1-2, 2-3. 4) Создайте первую фигуру. Это показывает твердый, веревочный многоугольник с prg-силой. 5) веревкой переходим к пересечению лучей a и w многоугольника и находим точку на линии действия результата. 6) нарисуйте результат через полученную точку, параллельную основному вектору силового многоугольника. При реш
ении задачи определения реакции твердой опоры в состоянии равновесия под действием»системы плоских сил» необходимо придерживаться следующей последовательности действий: 1) Нарисуйте твердое тело с активной силой на выбранном масштабе; 2) мысленно отбросьте опору и замените опору на нужную реакцию. 3) Создайте силовой полигон, где сумма требуемых реакций определяется на отдельном рисунке.
Смотрите также:
Предмет теоретическая механика
| Равновесие системы твердых тел | Система сходящихся сил |
| Равновесие тел при наличии трения | Произвольная пространственная система сил |

