Кручение круглого стержня

Оглавление:

Кручение круглого стержня

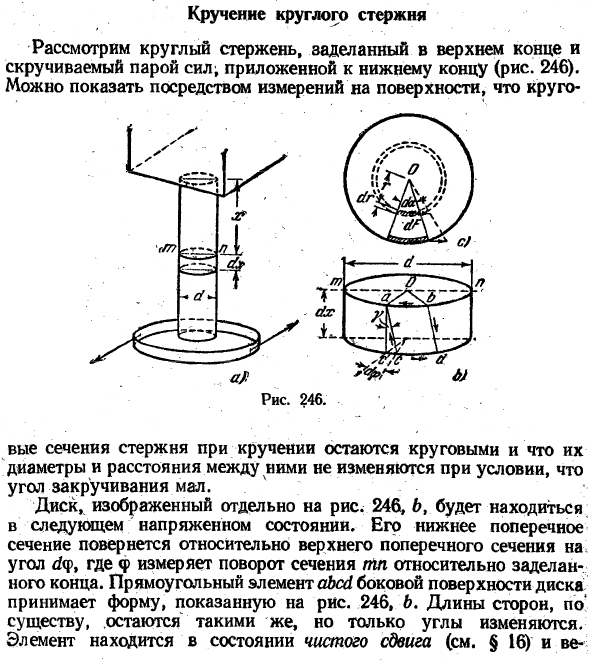
Круглая закрутка адвокатского сословия Рассмотрим круглый брус, врезанный в верхний край и скрученный парой сил. Прикрепите его к нижнему краю(рис. 246). это может быть указано через измерение поверхности Во время кручения поперечное сечение стержня остается круглым, и если угол кручения мал, то диаметр и расстояние между стержнями не изменяются. Диски 246 и 6, показанные отдельно на рисунке, находятся в следующих напряженных состояниях: нижняя секция повернута на угол.

Для стержня, скрученного моментом на конце, угол спирали пропорционален длине и значение dyldx равно constant. It представляет угол винтовой линии на единицу длины стержня и обозначается буквой В. Затем из (а) Г = г(в.(148)）. Касательное напряжение, действующее вдоль кромки элемента и вызывающее вышеуказанный сдвиг, будет в направлении, показанном на рисунке. Каждое значение основано на Формуле (39) Х = Y (149).

Что касается напряженного состояния внутри стержня, то предполагается, что круговой контур поперечного сечения стержня не искажается, но само поперечное сечение остается плоским и вращается как полностью твердое состояние, то есть каждый диаметр поперечного сечения вращается как прямая линия на один и тот же угол.

Поэтому напряженное состояние элементов на поверхности стержня хорошо изучено. Людмила Фирмаль

Тест круглого бара показывает, что теория, основанная на этом предположении, очень согласуется с экспериментальной results. In в этом случае обсуждение вдавленных элементов на поверхности штока (рис. 246, б) справедливо для аналогичных элементов поверхности внутреннего цилиндра, радиус которого T заменен на d / 2 (рис.246, в).

Толщина радиального элемента dr считается очень малой. Поэтому такие элементы также находятся в чистом сдвиговом состоянии, и касательное напряжение на их гранях равно ’.. Т = Гре.(Си） Это показывает его. Напряжение сдвига пропорционально расстоянию r от оси стержня. На рисунке 247 показано это распределение напряжений.

Наибольшее напряжение возникает на внешней поверхности rod. In в случае вязких материалов, поток пластика начинается на внешней поверхности. Для материалов с более слабым продольным сдвигом, чем поперечный, например, деревянных стержней с волокнами, параллельными оси, первая трещина возникает от напряжения сдвига, действующего на поперечное сечение в осевом направлении, и возникает на поверхности продольного стержня.

Для образцов материалов с меньшим напряжением, чем сдвиг, например, круглых чугунных стержней или цилиндрических дроссельных цилиндров, трещины часто возникают вдоль наклонной спирали под углом 45°к оси стержня(рис.248).Объяснение этому простое. Напомним, что состояние чистого сдвига соответствует растяжению в одном направлении и равно сжатию в вертикальном направлении(см. рис.45).

Прямоугольные элементы, вырезанные из наружного слоя скрученного стержня с боковой гранью под углом 45°к оси, подвергаются напряжениям, показанным на рисунке. 248.Указанное растягивающее напряжение создает спиральную трещину. Рисунок 247. Здесь мы находим связь между примененной витой парой Mk и напряжением, которое она вызывает.

Из равновесия частей стержня между днищем и поперечным сечением ТП (рис. 246, а) можно сделать вывод, что напряжение сдвига, распределенное в поперечном сечении, статически равно паре сил, равных и противоположных витой паре Mk. In каждому элементу области числа(рис.246, в) Сила сдвига равна mr. момент этого усилия для оси стержня по уравнению (в)равен (m ^ / 7) r = OoVY / \крутящий момент Mk равен сумме этих моментов, принятых по всему поперечному сечению.

Mk = 5 C6 / — * YҐ= C0 5 (с） Где J p-полярный момент инерции кругового по -. 248.Разрез. Для круга диаметром d см. Приложение A, стр. 353. Jp = id * l22t, следовательно м.= б 32. И затем М. (150） А, ndx-GJ.、 Можно видеть, что 0, который является углом спирали на единицу длины стержня, прямо пропорционален добавленному крутящему моменту Смотрите также: и обратно пропорционален модулю сдвига для 4-го и 4-го диаметров.

Если длина вала равна I, то формула суммы углов используется для экспериментальной проверки теории, подтверждая предположение, сделанное многочисленными допущениями при выводе теории. Отметим, что торсионные эксперименты обычно проводятся для определения модуля упругости различных материалов. Вы можете легко получить значение©из Формулы (151) путем измерения угла кручения, вызванного к определенному стержню определенным крутящим моментом.

Крутить будет Подставим в Формулу (150) 6 в Формулу(149) и получим формулу для расчета максимального касательного напряжения при кручении круглого стержня. х P521 млн ТТ * х-2 Максимальное касательное напряжение пропорционально крутящему моменту Mk и обратно пропорционально мощности 3 диаметра стержня.

В реальном применении, необходимый диаметр вала должен часто быть высчитан от количества лошадиной силы, котор нужно послать. Людмила Фирмаль

Для этого N крутящий момент в кг см выводится из известного уравнения Бизнес-класса 7500а/, (153） Здесь n означает число оборотов вала за 1 минуту. Значение 2yal / 60 представляет собой угловую скорость, левая часть уравнения (153)представляет работу, выполненную за 1 секунду крутящим моментом, измеренным в кг см, а правая часть уравнения представляет работу, рассчитанную по количеству лошадиных сил (кг см!).S) представляет собой M.

Если мы получим Mk из Формулы (153)и подставим его в Формулу (152), то получим следующую формулу: <1 {pm)= PMU■(154） Короткая клюшка Например, если допустимое напряжение сдвига составляет 1t 1 = 600 кг / см2、 СКМ)= = 8.43〜. Задачи 1.Для допустимого напряжения[t] = 200 кг/см2 определите диаметр вала машины n = 120 лошадиных сил при обороте / мин c1.

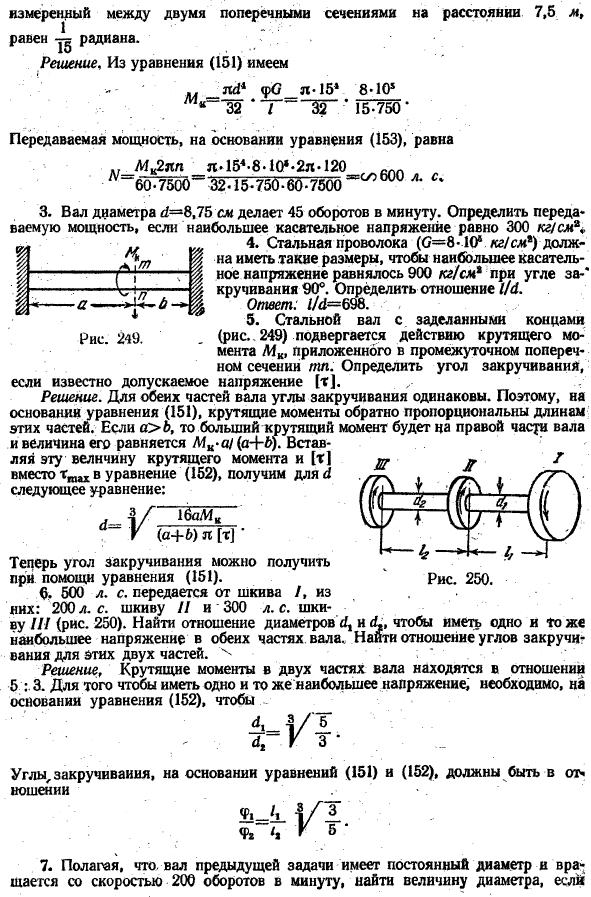
Ответ. £ / = 14,4 см 2. 15 см, p-120 об / мин, C = 8″ No. kg в случае / cmg и угла наклона спирали N* выход определяется мощностью, передаваемой валом. л Что? Я… ＆ € £ н. н. Я… Б. Я… Рисунок 251. [x 1 = 400. кг! см.* для d = * 8 «10 /. kg / cmи/,= / * = 1.2 m, найти спираль каждой части вала. 8.

Если максимальное напряжение составляет 900 кг, то диаметр (1 = 5 см ()) определите длину стального вала!См, когда угол винтовой линии равен 6 Ответ. / = 2,33 м 9. 6 = 8 » 10 * кг!Для см *, [г 1 = 200 кг] см *и с максимально допустимым углом кручения 1, угол кручения вала, а не максимальное напряжение, определяет диаметр, который важен в конструкции. / 46 на метр. Решение.Исключить Mk из уравнения Получает (/=11.46 см, и поэтому + Л1 ^ / Канзас. МКА. МК + МК<» + > / 11.Задача 6 определите диаметр и угол закрутки вала. n — = 120 оборотов в минуту, tm = 200 кг! См,/, = 1,8 м и / * = 1,2 м \

Кручение полого вала	Расчет колонн на основании предполагаемых неточностей
Вал прямоугольного поперечного сечения	Эмпирические формулы для расчета колонн