Оглавление:




Критическое напряжение. Расчет колонн
Принимая во внимание случай стойки с шарнирным концом, получим критическое напряжение путем деления критической нагрузки, определяемой по формуле (145), на площадь поперечного сечения. Найдите его таким образом < з — (147) Для данного материала видно, что величина критического напряжения зависит от величины отношения я, которое называется стержнем стерж.
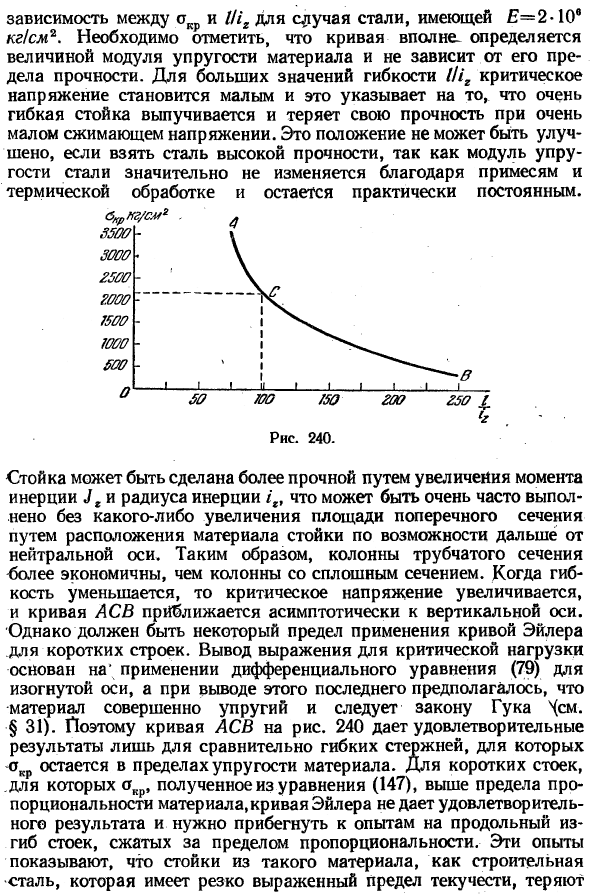
- Рисунок 240, кривая DIA представляет собой Я. \•л. 0 таким образом, R. V. S A u t h w e 1 Rum Proc. Рой. Соц. (Лондон) и » т. к.135, стр. 601, 1932 ″ оказался очень полезным и в настоящее время широко используется в испытаниях колонн. а) поскольку эта кривая иногда называется кривой Эйлера, канон получается из Формулы Эйлера критической нагрузки. £=2-10®кг / см2, Wr соединение с ОКР в случае стали.
Отметим, что кривая полностью определяется модулем упругости материала и не зависит от его прочности на растяжение. При большом значении гибкости 1 НГ критическое напряжение мало, что указывает на то, что очень гибкая стойка выпячивается и теряет свою прочность при очень малом напряжении сжатия. Это положение не может быть улучшено, если используется высокопрочная сталь.
Это объясняется тем, что модуль упругости стали существенно не изменяется из-за примесей или термической обработки и остается практически постоянным. Стенд можно сделать более прочным за счет увеличения момента инерции Jr и радиуса инерции. Это можно сделать без увеличения площади поперечного сечения, поместив материал на подставку как можно дальше от нейтральной оси.
Поэтому колонны трубчатого сечения более экономичны, чем колонны непрерывного сечения columns. As гибкость уменьшается, критическое напряжение увеличивается, и кривая ASB приближается к вертикальной оси асимптотически. Однако существуют некоторые ограничения на применение кривых Эйлера с короткими структурами.
Вывод формулы критической нагрузки основан на применении дифференциальных уравнений (79) к оси кривой, и если это выводит последнее, то предполагалось, что материал полностью упруг и подчиняется закону хукена нема. § 31).Таким образом, Диа-кривая на рисунке равна 240, что дает удовлетворительный результат только для относительно гибких стержней, где ОКР находится в пределах упругого диапазона материала.
Если площадь, полученная из уравнения (147), является более короткой стойкой выше пропорционального предела материала, кривая Эйлера не даст удовлетворительных результатов, и необходимо прибегнуть к экспериментам вертикального изгиба на стойках, которые были сжаты за пропорциональным пределом. Людмила Фирмаль
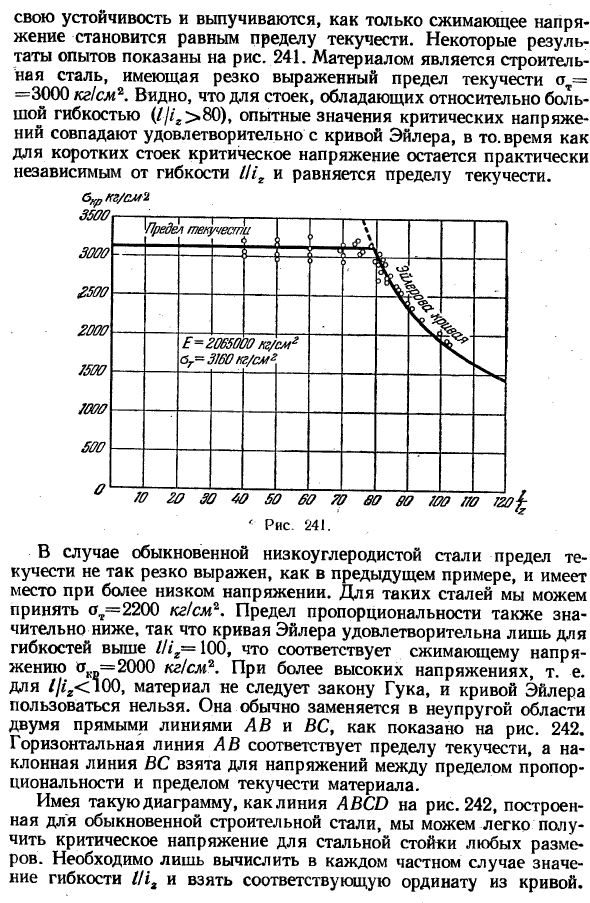
Эти эксперименты показывают, что как только напряжение сжатия становится равным пределу текучести, стеллажи из таких материалов, как строительная сталь, которые имеют ярко выраженный предел текучести, теряют свою устойчивость и разбухают. Некоторые экспериментальные результаты представлены на рисунке. 241.
Материал структурная сталь и имеет замечательную прочность выхода от= 3000 kg1cm2.В относительно гибкой стойке (/•//*>80), вы можете видеть, что экспериментальное значение критического напряжения на самом деле хорошо соответствует кривой Эйлера. С другой стороны, для коротких стоек критическое напряжение практически не зависит от гибкости Wr и равно пределу текучести. — Рисунок 241.
Для обычных низкоуглеродистых сталей предел текучести не так выражен, как в предыдущем примере, и он возникает при низких напряжениях. За такую сталь можно взять= 2200 кг! См2. Пропорциональный предел также намного ниже, поэтому кривая Эйлера равна a = 2000 кг! Это удовлетворительно только для гибкости, которая превышает W-100, что соответствует напряжению сжатия Cm2.At при более высоком напряжении, то есть///,< * 00, материал не подчиняется закону крюка, и кривые Эйлера не могут быть used.
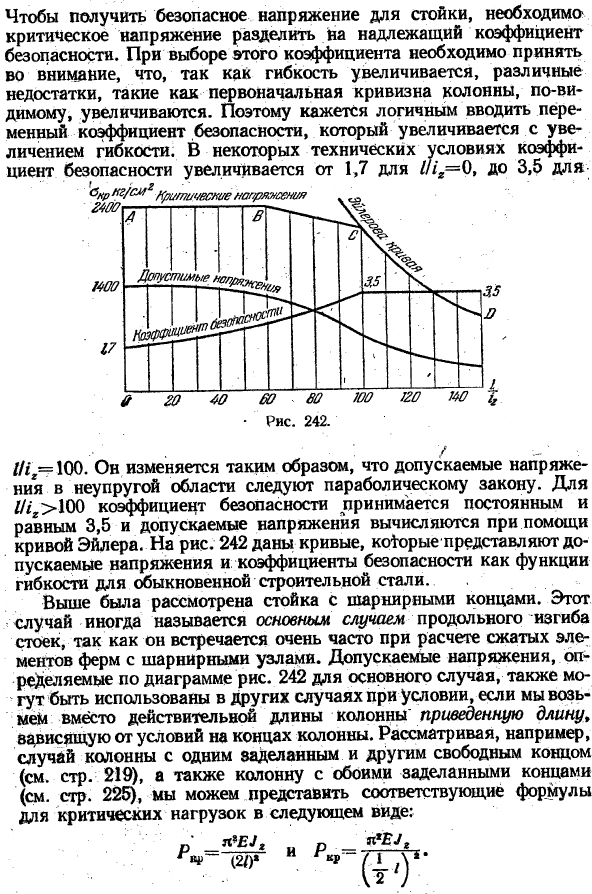
Как показано на рисунке, неупругие области обычно заменяются 2 прямыми линиями A B и BC. 242.Горизонтальная линия A B соответствует пределу текучести, а наклонная линия BC берется против напряжения между пропорциональным пределом материала и пределом текучести. Имея диаграмму, подобную линии LANO на рисунке 242, он построен для стали нормального здания, поэтому вы можете легко получить критическое напряжение стальных стоек любого размера.
Просто вычислите значение гибкости Wx для каждого конкретного случая и получите соответствующую ординату из curve. To чтобы получить безопасное напряжение для стойки, необходимо разделить критическое напряжение на соответствующий коэффициент безопасности.
- При выборе этого коэффициента следует учитывать, что с увеличением гибкости, по-видимому, увеличиваются различные недостатки, такие как кривизна первого столбца. Поэтому представляется логичным ввести переменные коэффициенты безопасности, которые увеличиваются с увеличением flexibility.
В некоторых спецификациях коэффициент запаса прочности///,= 0 увеличивается с 1,7 до 3,5. , <ГСЧ / СМГ * Рисунок 242. Ш-100.Допустимое напряжение в неупругой области изменяется в соответствии с параболическим законом. При 1 / 1g> 100 коэффициент запаса прочности принимается равным 3,5, а допустимое напряжение рассчитывается с использованием кривой Эйлера.
На рисунках приведены 242 кривые, которые представляют собой допустимые напряжения и коэффициент запаса прочности в зависимости от гибкости обычной строительной стали. Выше была рассмотрена стойка с шарнирами на обоих ends. In этот случай иногда называют основным случаем продольного изгиба вертикального материала, так как он очень распространен при расчете элементов сжатия ферм с шарнирными узлами.
Вместо фактической длины допустимого напряжения столба, как определено на рисунке на рисунке, 242 может также использоваться для основного случая, при условии, что длина уменьшается в 2 раза от размера условия в конце столбца. Например, формула, соответствующая критической нагрузке, может быть представлена в следующем виде с учетом случая колонны, в которой один конец запечатан, а другой конец открыт (см. стр. 219), а другой конец запечатан (см. стр. 225).: п л * ejt не п _ «*>(2/) * » П / Я Д4 *
Если сравнить эти формулы с формулой основного случая (145), то можно сделать вывод, что если вычислить столбец, в котором один вложен, а другой является свободным концом, то для использования фигуры 242 нам потребуется в 2 раза больше фактической длины. Для колонки с обоими загерметизированными концами, укороченная длина половина фактической длины. Людмила Фирмаль
Выбор соответствующих размеров поперечного сечения колонны обычно производится путем последовательных испытаний. Поскольку мы знаем нагрузку P, которая действует на колонну, мы берем некоторые размеры сечения и вычисляем Jg и UiK для этих размеров. Значение безопасного напряжения сжатия затем берется из диаграммы. 242.
Если это значение умножить на допустимую площадь поперечного сечения, то получается допустимая нагрузка на колонну. Если эта нагрузка не падает ниже P и немного больше, то допустимое сечение удовлетворительно. В противном случае расчет придется повторить. Если торцом является герметичная колонна, то при расчете ix учитывается общее поперечное сечение. это связано с тем, что отверстия в заклепке существенно не влияют на критическую нагрузку.
Однако при расчете безопасной нагрузки на колонну допустимое напряжение умножается на площадь чистого поперечного сечения, чтобы гарантировать отсутствие чрезмерного напряжения в колонне. Задачи 1.Стальной стержень с прямоугольным поперечным сечением 2,5 х см, концы которого соединены, сжимается под действием продольной силы.
Если предел пропорциональности материала составляет 2000 кг / см *и Е = * = 2•10 кг / см2, то определяют самую короткую длину, которую формула (147) может применить к критическому напряжению. Если длина стержня составляет 1,5 м, определите критическое значение напряжения. Ответ. Минимальная длина составляет » 72 см.«/Критическое напряжение составляет » 1,5 л. 457 кг / см2. 。 2.
Решаем предыдущую задачу, предполагая, что стержень имеет круглое поперечное сечение диаметром 2,5 см, а концы герметизированы. 3.Длина. Определить критическое / сжимающее напряжение балки двутаврового сечения, равной 1,8 м и герметизированной с обоих концов. «=64,4 см€, Jy= 712 см, F » 21,5 см2.
Используйте кривые рисунка для определения безопасной нагрузки. 242. Ответ. АКО = 1830 кг / см2,///, «104, безопасная нагрузка» = 11,240 / С Р 4.Решите предыдущую задачу, предположив, что края колонны герметичны. Воспользуйтесь фотографиями. 242. Ответ. ОКР = «2200 кг / см*, коэффициент запаса» = 2, безопасность нагрузка= 23 650 кг. Рисунок 243. 5.
Используйте диаграмму для расчета. 242 безопасная нагрузка Для стержня (рис.243), состоящего из 2 двутавровых балок с тем же поперечным сечением, что и в задаче 3 выше. Длина стержня составляет 3 л, с шарнирным концом. Предположим, что соединение очень жесткое, и оба двутавровых луча работают как 1 Луч. Решение. Y * = 2X 712 = 1424 cl4,= 2 [64,4 + 21,5 X (5) 2] = 1204 см *.
Поэтому большое значение гибкости }-300 −567 ул, гш ’» Г 2-21. Пять На рисунке показано, что допустимое напряжение сжатия 242 составляет 1030 кг / см2. Предохранительная нагрузка= 1030 * 2.21.5 = 44 300 кг 6.Мы решаем предыдущую задачу, предполагая, что оба конца стержня герметичны. 7.Шарнирная колонна длиной 3G состоит из 2 каналов JZ = 53,2 см4, Y» = 563,7 см4, T7 = 18,51 см2, центра тяжести и расстояния r0 = 1 между наружной поверхностью стенки канала. 71 см.
Если расстояние между наружными поверхностями стенок канала составляет 10 см, найдите безопасную нагрузку в колонне. 8.Если нагрузка равна Р = 16 т, а оба конца закреплены шарниром, Определите необходимое квадратное сечение стальной стойки длиной 1,8 м. воспользуйтесь фотографиями. 242. 9.It решает предыдущую проблему, предполагая, что оба конца стойки запечатаны.
Смотрите также:
Предмет сопротивление материалов: сопромат
| Расчет колонн на основании предполагаемых неточностей | Внецентренное сжатие гибкой симметричной колонны |
| Эмпирические формулы для расчета колонн | Критическая нагрузка |

